Shortcut Estimation of Temperature Effects

Recall Eqn. 17.25, which we refer to as the general van’t Hoff equation:

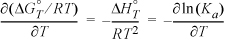
We can make rapid estimates of the equilibrium constant when we make the approximation that ΔH_T^o is independent of temperature. That is, suppose ΔC_P = Δa = Δb = Δc = Δd = 0, which means the sensible heat effects for the reactants and products are the same. This is most closely approximated when all species are about the same molecular size and the same state of aggregation. With this approximation,  in Eqn. 17.27, or we can integrate Eqn. 17.25 directly to obtain what we refer to as the shortcut van’t Hoff equation:

 Shortcut van’t Hoff equation.

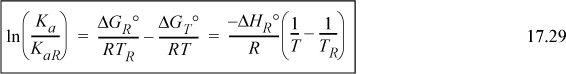
This equation enables rapid screening for the effects of temperature and the detailed van’t Hoff can be used as a follow-up calculation. As a particular observation, we take special note from the above equation that exothermic reactions (ΔH_T < 0) lead to K_a decreasing as temperature increases, and endothermic reactions (ΔH_T > 0) lead to K_a increasing as temperature increases. This means that equilibrium conversion (for a specified feed) decreases with increasing temperature for exothermic reactions, and increases for endothermic reactions. This effect is illustrated in Fig. 17.1. The emphasis is placed on equilibrium because reaction rates increase with temperature. Industrial application of exothermic reactions are almost always run at elevated temperatures even though the equilibrium constant decreases at high temperature. For all reactions, the reaction rate will approach zero as equilibrium is approached. The benefit of faster kinetics typically outweighs the smaller equilibrium constant for exothermic reactions when economics are considered. There connection between equilibrium constants and kinetic rates that approach zero is explained in Section 17.15.

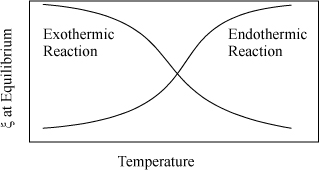
Figure 17.1. Qualitative behavior of equilibrium conversion for exothermic and endothermic reactions.

The approximate results of the shortcut van’t Hoff equation should be followed with the detailed van’t Hoff for critical applications. To improve shortcut estimates, the detailed van’t Hoff can be used at T_near within 100 K of the temperatures of interest to calculate ΔG_Tnear^o and ΔH_Tnear^o. Then the values at T_near can be used as the reference values in Eqn. 17.29.

---

Example 17.5. Application of the shortcut van’t Hoff equation

Apply the shortcut approximation to the vapor phase hydration of ethylene. This reaction has been studied in the previous example, and the Gibbs energy of reaction and heat of reaction can be obtained from that example.

Solution

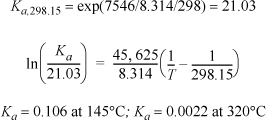
The results are very similar to the answer obtained by the general van’t Hoff equation in Example 17.4.