We found that the Clausius-Clapeyron equation leads to a simple, two-constant equation for the vapor pressure at low temperatures. What about higher temperatures? Certainly, the assumption of ideal gases used to derive the Clausius-Clapeyron equation is not valid as the vapor pressure becomes large at high temperature; therefore, we need to return to the Clapeyron equation. If ΔHvap/ΔZvap was constant over a wide range of temperature, then we could recover this simple form. Obviously, ΔZvap is not constant; as we approach the critical point, the vapor and liquid volumes get closer together until they eventually become equal and ΔZvap → 0. However, the enthalpies of the vapor and liquid approach one another at the critical point, so it is possible that ΔHvap/ΔZvap may be approximately constant. To analyze this hypothesis, let us plot the experimental data in the form of Eqn. 9.7 assuming that ΔHvap/ΔZvap is constant. A constant slope would confirm a constant value of ΔHvap/ΔZvap. A plot is shown for two fluids in Fig. 9.1.
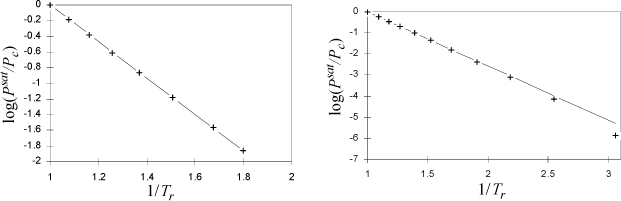
Figure 9.1. Plot to evaluate Clausius-Clapeyron for calculation of vapor pressures at high pressures, argon (left) and ethane (right).
The conclusion is that setting ΔH/ΔZ equal to a constant is a reasonable approximation, especially over the range of 0.5 < Tr < 1.0. The plot for ethane shows another nearly linear region for 1/Tr > 2 (temperatures below the normal boiling temperature), with a different slope and intercept. The approach of the previous section should be applied at Tr < 0.5. Integrating the Clapeyron equation for vapor pressure, we obtain,
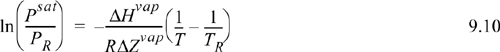
The plot of lnPsat versus 1/T is nearly linear.
Example 9.2. Vapor pressure interpolation
What is the value of the pressure in a piston/cylinder at –12°C (261.2 K) with vapor and liquid propane present? Use only the boiling temperature (available from a handbook), critical properties, and acentric factor to determine the answer.
Solution
We will use the boiling point and the vapor pressure given by the acentric factor to determine (–ΔHvap)/(RΔZvap) for Eqn. 9.10, and then use the boiling temperature with (–ΔHvap)/(RΔZvap) to determine the desired vapor pressure. First, let us use the acentric factor to determine the vapor pressure value at Tr = 0.7. For propane, Tc = 369.8 K, Pc = 4.249 MPa, and ω = 0.152. Solving for the vapor pressure in terms of MPa by rearranging the definition of the acentric factor, 
MPa.a The temperature corresponding to this pressure is T = Tr·Tc = 0.7·369.8 = 258.9 K. The CRC handbook lists the normal boiling temperature of propane as –42°C = 231.2 K. Using these two vapor pressures in Eqn. 9.10:
ln(0.2994/0.1013) = –ΔHvap/(RΔZvap)(1/258.9 – 1/231.2) ⇒ –ΔHvap/(RΔZ) = –2342 K
Therefore, using the boiling point and the value of –ΔHvap/(RΔZvap),
Psat(261.2 K) = 0.1013 MPa · exp[–2342(1/261.2 – 1/231.2)] = 0.324 MPa
The calculation is in excellent agreement with the experimental value of 0.324 MPa.
a. Could we use the Clausius-Clapeyron equation at this condition? Since the Clausius-Clapeyron equation requires the ideal gas law, the Psat value must be low enough for the ideal gas law to be followed. The deviations at this state can be quickly checked with the virial equation, Pr = 0.07, Tr = 0.7, B0 = –0.664, B1 = –0.630, Z = 0.924; therefore, the Clausius-Clapeyron equation should probably not be used. Although you would get the same answer for vapor pressure over this narrow range, your inaccurate estimate of ΔHvap might mislead you in a later calculation.
Since the linear relationship of Eqn. 9.10 applies over a broad range of temperatures, we can derive an approximate general estimate of the saturation pressure based on the critical point as the reference and acentric factor as a second point on the vapor pressure curve.
Setting PR = Pc and TR = Tc,
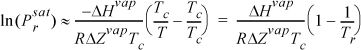
Common logarithms are conventional for shortcut estimation, possibly because they are more convenient to visualize orders of magnitude.
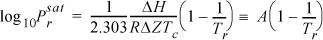
Relating this equation to the acentric factor defined by Eqn. 7.2,
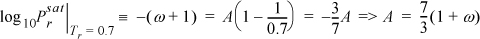
which results in a shortcut vapor pressure equation,
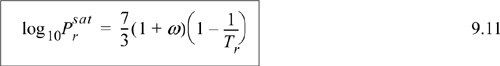
Shortcut vapor pressure equation. Use care with the shortcut equation below Tr = 0.5.
Note: The shortcut vapor pressure equation must be regarded as an approximation for rapid estimates. The approximation is generally good above P = 0.5 bar; the percent error can become significant at lower pressures (and temperatures). Keep in mind that its estimates are based on the critical pressure which is generally 40–50 bar and acentric factor (at Tr = 0.7).
Example 9.3. Application of the shortcut vapor pressure equation
Use the shortcut vapor pressure equation to calculate the vapor pressure of propane at –12°C, and compare the calculation with the results from Example 9.2.
Solution
For propane at –12oC, Tr = 261.2/369.8 = 0.7063,
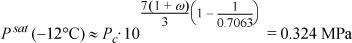
This is in excellent agreement with the result of Example 9.2, with considerably less effort.
Example 9.4. General application of the Clapeyron equation
Liquid butane is pumped to a vaporizer as a saturated liquid under a pressure of 1.88 MPa. The butane leaves the exchanger as a wet vapor of 90 percent quality and at essentially the same pressure as it entered. From the following information, estimate the heat load on the vaporizer per gram of butane entering.
For butane, Tc = 425.2 K; Pc = 3.797 MPa; and ω = 0.193. Use the shortcut method to estimate the temperature of the vaporizer, and the Peng-Robinson equation to determine the enthalpy of vaporization.
Solution
To find the T at which the process occurs:a
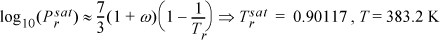
First, we use the Peng-Robinson equation to find departure functions for each phase, and subsequently determine the heat of vaporization at 383.2 K and 1.88 MPa:
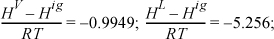
Therefore, ΔHvap = (–0.9949 + 5.256)8.314·0.90117·425.2 = 13,575 J/mol
Since the butane enters as saturated liquid and exits at 90% quality, an energy balance gives Q = 0.9·13,575 = 12,217 J/mol ·1mol/58g = 210.6 J/g
Alternatively, we could have used the shortcut equation another way by comparing the Clapeyron and shortcut equations:
Clapeyron: ln(Psat) = –ΔHvap/RT(ZV – ZL) + ΔHvap/RTc(ZV – ZL) + lnPc
Shortcut: 
Comparing, we find: 
Therefore, using the Peng-Robinson equation at 383.3 K and 1.88 MPa to determine compressibility factor values,
ΔHvap = 2725R (ZV – ZL) = 2725(8.314)(0.6744 – 0.07854) = 13,500 J/mol
which would give a result in good agreement with the first approach.
a. In principle, since we are asked to use the Peng-Robinson equation for the rest of the problem, we could have used it to determine the saturation temperature also, but we were asked to use the shortcut method. The use of equations of state to calculate vapor pressure is discussed in Section 8.10.
The Antoine Equation
The simple form of the shortcut vapor-pressure equation is extremely appealing, but there are times when we desire greater precision than such a simple equation can provide. One obvious alternative would be to use the same form over a shorter range of temperatures. By fitting the local slope and intercept, an excellent fit could be obtained. To extend the range of applicability slightly, one modification is to introduce an additional adjustable parameter in the denominator of the equation. The resultant equation is referred to as the Antoine equation:
Antoine equation. Use with care outside the stated parameter temperature limits, and watch use of log, ln, and units carefully.
where T is conventionally in Celsius.2 Values of coefficients for the Antoine equation are widely available, notably in the compilations of vapor-liquid equilibrium data by Gmehling and coworkers.3 The Antoine equation provides accurate correlation of vapor pressures over a narrow range of temperatures, but a strong caution must be issued about applying the Antoine equation outside the stated temperature limits; it does not extrapolate well. If you use the Antoine equation, you should be sure to report the temperature limits as well as the values of coefficients with every application. Antoine coefficients for some compounds are summarized in Appendix E and within the Excel workbook Antoine.xlsx.
Antoine.xlsx and Matlab/Props have coefficients for many common substances.
Leave a Reply