Scatchard-Hildebrand Theory

Returning to Eqn. 12.10, G. Scatchard in Europe and Joel H. Hildebrand in the United States both made similar adjustments to match the van der Waals equation to experiment and provide a model capable of predictions for nonpolar fluids. They made an assumption that is equivalent to assuming k₁₂ = 0 in Eqn. 12.4. Setting , and collecting terms,

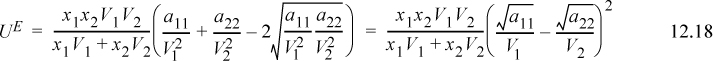
J.H. Hildebrand is credited with suggesting that helium be mixed with breathing air in deep sea diving to minimize “the bends.” He was awarded the ACS Priestly award in 1962. He continued to maintain an active professional life until he was 100.

Scatchard and Hildebrand recognized the unknown parameters in terms of volume fractions and disperse attraction energies that could be related to the pure component values. Defining a term called the “solubility parameter,”

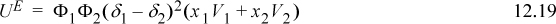
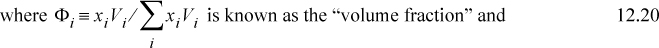
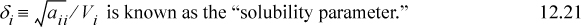
To estimate the value of δ_i, Scatchard and Hildebrand suggested that experimental data be used such that

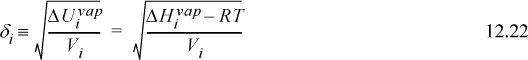
(Note the units on the “a” parameter from Eqn. 12.2, and from comparing Eqns. 12.21 and 12.22, and note the way V_i moves inside the root in Eqn. 12.22.)

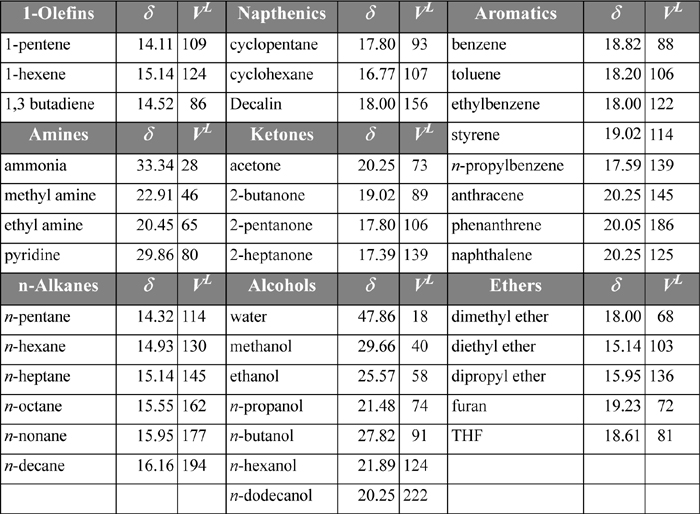
In other words, δ_i is assumed to provide a standard measure of the “energy density” for each component. Because it represents the energy departure divided by volume, it is called the cohesive energy density. As long as a standard reference condition is used, any convenient set of ΔU^vap and V_i may be applied. A convenient set of conditions that has become customary is the saturated liquid at 298 K. On this basis, we can tabulate a fair number of solubility parameters for ready reference, as shown in Table 12.1. Note that many similar compounds have similar values for their solubility parameters. Since similar solubility parameters yield small excess energies, solutions of similar components are predicted to be nearly ideal, as intuitively expected. By scanning the tables for the values of solubility parameters, we can quickly estimate whether the ideal solution model should be accurate or not. This approach gives a quantitative flavor to the old adage “like dissolves like.”

Table 12.1. Solubility Parameters in (J/cm³)^1/2 and Molar Volumes (cm³/mol) for Various Substances as liquids at 298 K

Turning to the Gibbs energy, the regular solution assumptions give,

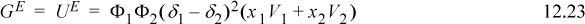
And the resultant activity coefficients are

 Scatchard-Hildebrand theory.

 Actcoeff.xlsx, worksheet REGULAR.

 Bubble-temperature calculation.

---

Example 12.2. VLE predictions using the Scatchard-Hildebrand theory

Benzene and cyclohexane are to be separated by distillation at 1 bar. Use the Scatchard-Hildebrand theory to predict whether an azeotrope should be expected for this mixture.

Solution

We will implement the algorithm to test for an azeotrope from Section 11.7 on page 432. Given x_B and P, we should perform bubble-temperature calculations.

Using parameters from Table 12.1, at x_B = 0.99, guess T = 350 K:

⇒ Φ_B = 0.99(88)/[0.99(88) + 0.01(107)] = 0.9879

Calculating vapor pressures:

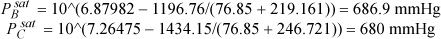
Applying Eqns. 12.24 and 12.25:

lnγ_B = 88(1 – 0.9879)²(18.74 – 16.75)²/(8.314·350) = 1.8E-5 ⇒ γ_B = 1.00002
lnγ_C = 107(0.98789)² (18.74 – 16.75)²/(8.314·350) = 0.1443 ⇒ γ_C = 1.1552

Calculating the pressure and vapor mole fractions:

 = 0.99(1.00)(686.9) + 0.01(1.1552)(680.0) = 687.9 mmHg

⇒y_B = 0.99(1.00)(686.9)/687 = 0.895, y_C = 0.01(1.1552)(680.0)/687 = 0.010

Since , we must guess a higher temperature.

Guess T = 354 K ⇒ ; ; γ_B = 1.00; γ_C = 1.1533

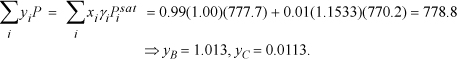
Interpolating between the first guesses:

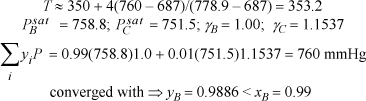
At x_B = 0.01, guess T = 353.5 K ⇒ Φ_B = 0.01(88)/[0.01(88) + 0.99(107)] = 0.0082

lnγ_C = 107(0.0082)²(18.74 – 16.75)²/(8.314·350)≈ 0 ⇒ γ_C = 1.00
lnγ_B = 88(1 – 0.0082)²(18.74 – 16.75)²/(8.314·350) = 0.1232 ⇒ γ_B = 1.126

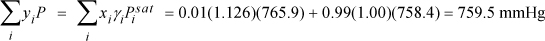
converged with ⇒ y_B = 0.011 > x_B = 0.01

Therefore, (y_B – x_B) changes sign between 0.01 and 0.99, so the system has an azeotrope.

---

 Actcoeff.xlsx, worksheet REGULAR.

When the Scatchard-Hildebrand solution theory is used, the {δ_i} and {V_i} are available directly from pure component data, and in principle, there are no adjustable parameters. The theory is entirely predictive. The van Laar theory, on the other hand, treats both A₁₂ and A₂₁ as adjustable parameters. We can also obtain a compromise by assuming

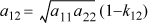
The activity coefficient expressions for binary solutions become:

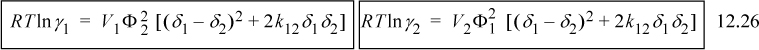
 Scatchard-Hildebrand model with an adjustable parameter.

In mixtures of compounds that deviate moderately from ideal-solution behavior, the Scatchard-Hildebrand solution theory with binary interaction parameters can be extremely helpful. The binary interaction parameter in those cases serves to adjust the magnitude of the excess Gibbs energy without addressing the skewness directly. Large deviations, however, are generally accompanied by non-ideal mixing in the volume and entropy. In those cases, the van Laar equations can often be useful in correlation, but the physical meaning behind the parameters is generally lost.

Paul J. Flory was awarded the Nobel Prize in chemistry in 1974. The original derivation used statistical mechanics, but is consistent with this alternative derivation.