P19.1.
a. A gas-phase A+B system solvates A + B 
AB with Ka = 0.5 at 298.15 K. Calculate the compressibility factor, apparent fugacity coefficients, and the true vapor phase mole fractions in a mixture at 298.15 K and 2 bar when the apparent concentration is yA = 0.45 using ideal chemical theory.
b. A liquid-phase A+B system solvates A + B AB with Ka = 0.7 at 298.15 K. Calculate the true liquid-phase mole fractions in a mixture at 298.15 K and 1 bar when the apparent concentration is xA = 0.45 using ideal chemical theory.
c. A gas-phase A+B system associates 2A A2 with Ka = 0.5 at 298.15 K. Calculate the compressibility factor, apparent fugacity coefficients, and the true vapor phase mole fractions in a mixture at 298.15 K and 2 bar when the apparent concentration is yA = 0.45 using ideal chemical theory.
19.14. Homework Problems
19.1. Consider a dilute isothermal mixing process of acetic acid(1) in benzene(2). For the dilute region (say, up to 5 mol% acid), draw schematically curves for the following:
versus x1; 
versus x1; 
versus x1.
Briefly justify your schematic graphs with suitable explanations. Take standard states as the pure substances.
19.2. Acetic acid dimerizes in the vapor phase. Show that the fugacity of the dimer is proportional to the square of the fugacity of the monomer.
19.3. By assuming that the equilibrium constant for each successive hydrogen bond is equal in the generalized association approach developed in this chapter, what assumptions are being made about the Gibbs energy, enthalpy, and entropy for each successive hydrogen bond?
19.4. The value of the excess Gibbs energy at 298 K for an equimolar chloroform(1) + triethylamine(2) system is GE = –0.91 kJ/mol. Assuming only a 1-1 compound is formed, model the excess Gibbs energy with ideal chemical theory, and plot the P-x-y diagram.
19.5. Suppose that, due to hydrogen bonding, the system A + B forms a 1-1 complex in the vapor phase when mixed. Neither pure species self-associates in the vapor phase. The equilibrium constant for the solvation is KAB = 0.8 bar–1 at 80°C. At 80°C, a mixture with a apparent (bulk) mole fraction of yA = 0.5 is all vapor at 0.78 bar. Calculate the fugacity coefficient of A in the vapor phase using ideal chemical theory at this composition, temperature, and pressure. Use hand calculations.
19.6. At 143.5°C, the vapor pressure of acetic acid is 2.026 bar. The dimerization constant for acetic acid vapor at this temperature is 1.028 bar–1. The molar liquid volume of acetic acid at this temperature is 57.2 cm3/mol. Calculate the fugacity of pure acetic acid at 143.5°C and 10 bar. Use hand calculations.
19.7. An A + B mixture exhibits solvation in the liquid phase, which is to be represented using ideal chemical theory. Because of a Lewis acid/base interaction, the system is expected to form a 1-1 compound.
a. Which one of the following sets of true mole fractions are correct for the system using an equilibrium constant of 3.2 to represent the complex formation at an apparent composition xA = 0.4?
b. Based on your answer for part (a), what are the apparent activity coefficients of A and B?
19.8. Water and acetic acid do not form an azeotrope at 760 mmHg. The normal boiling point of acetic acid is 118.5°C. Therefore, at 118.5°C and 760 mmHg, the mixture will exhibit only vapor behavior across the composition range. The following equilibrium constants have been fitted to represent the vapor-phase behavior:34
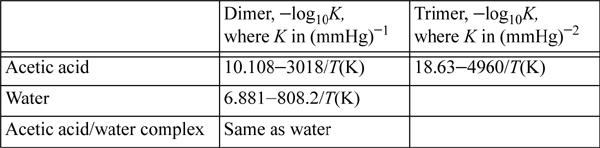
a. Let compound A be acetic acid and B be water. Calculate the true mole fractions of all the species from yA = 0.05 to yA = 0.95. At what apparent mole fraction does each specie show a maximum true mole fraction? What is the relation of this apparent mole fraction with the compound’s stoichiometry?
b. Plot the fugacity coefficient of acetic acid and water as a function of acetic acid mole fraction. What is the physical interpretation of the rapid change of the acetic acid fugacity coefficient in the dilute region, if the water fugacity coefficient doesn’t show such a dramatic trend in its dilute region?
a. The molar Gibbs energy of mixing (per mole of superficial solution) for a liquid binary system
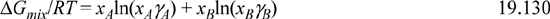
expressed extensively, this becomes
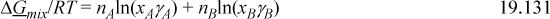
Introduce the concepts of chemical theory into Eqn. 19.131 to prove that the Gibbs energy of mixing is equivalently given by the sums over true species,
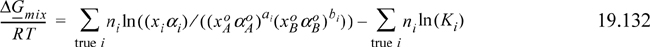
where Ki is unity for the monomers. Hint: nA = ∑aini.
b. Show that on a molar basis for an ideal chemical theory solution that has only solvation, per mole of true solution, the equation reduces to
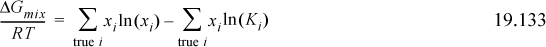
and provide a physical interpretation relating the Gibbs energy of formation to K.
c. Considering a system where A associates, show that the Gibbs energy of mixing by ideal chemical theory is per mole of true solution given by
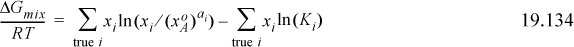
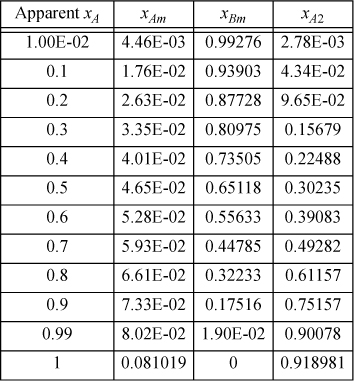
Below are tabulated calculations for ideal chemical theory for an A + B system where A forms dimers with K=140. Use Eqns. 19.134 and 19.130 to tabulate the respective Gibbs energies of mixing over RT. Then tabulate nT/n0 (the number of true moles divided by the number of apparent moles) and multiply Eqn. 19.134 by this number and compare with Eqn. 19.130.
19.10. Furnish a proof that the concentration of true species i is maximum at composition xA* = ai/(ai + bi), xB* = bi/(ai + bi) where ai and bi are given in Eqn. 15.1. [Hint: The Gibbs-Duhem equation is useful for relating derivatives of activity.]
19.11. Show that the result for Zassoc is obtained by taking the appropriate derivative of Aassoc.
19.12. Use the ESD equation to model the monomer, dimer, and trimer in the vapor and liquid phases of saturated water at 373 K, 473 K, and 573 K. How does the monomer fraction of saturated vapor change with respect to temperature? How does monomer fractions of saturated liquid change?
19.13. Derive the equations for determining the critical point of the ESD equation35 based on εHB and KAD being zero by noting that dF/dZ = 0 and d2F/dZ2 = 0, where F = Z3 + a2Z2 + a1Z + a0 when hydrogen bonding is negligible.
19.14. Plot P against V at 647.3 K for water with the ESD equation using the characterization analogous to Eqns. 15.73–15.76. Apply the equal area rule and determine the vapor pressure at that temperature. Raise the temperature until the areas equal zero and compare this temperature to the true value of 647.3 K.
19.15. Apply the ESD equation to the methanol + benzene system and compare to the data in Perry’s Handbook based on matching the bubble pressure at the azeotropic point. Prepare a T-x–y diagram and determine whether the ESD equation indicates a liquid-liquid phase split for any temperatures above 250 K. Perform the same analysis for the Peng-Robinson EOS. Do you see any differences? Compare to Fig. 15.3 on page 599.
19.16. Use the ESD equation to estimate the mutual LLE solubilities of methanol and n-hexane at 285.15 K, 295.15 K, and 310.15 K. Use the value of kij = 0.03 as fitted to a similar system in Fig. 19.12 on page 804.
19.17. The hydrogen halides are unusual. For example, here are the critical properties of various hydrogen halides:
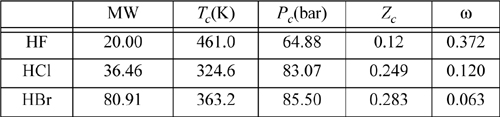
Experimental data for the vapor pressure and the apparent molecular weight of HF vapor are as follows:
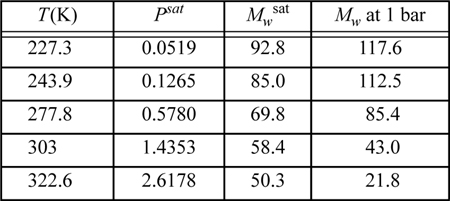
These apparent molecular weights have been found by measuring the mass density of the vapor and comparing with an ideal gas of molecular weight 20. Assuming that HF forms only monomers and hexamers, use the ESD EOS with c = q = 1 for both monomer and hexamer to match this value of Zc, and fit the vapor density data as accurately as possible in the least squares sense.
a. Compute the values of Ka´, a/bRTc, xMc, and bρc for methanol and ethanol according to the van der Waals hydrogen bonding equation of state.
b. Assuming an enthalpy of hydrogen bonding of 24 kJ/mole and ΔCP = –R, calculate the acentric factors for methanol and ethanol according to the vdw-HB EOS.
19.19. Derive the association model for the Peng-Robinson model, using the van’t Hoff formula with ΔCP/R = –1. Extend the homomorph concept by applying ωPR = ωhomo, where ωhomo is the acentric factor for the nonassociating homomorph and ωPR is the acentric factor substituting for the associating compound into the Peng-Robinson expression for a.
a. For methanol, determine the values of Ka′, b, a/bRTc, xMc that match the critical point.
b. Determine the vapor pressure at Tr = 0.7 for methanol assuming a hydrogen bonding energy of 15 kJ/mole, and compare to the experimental value. Infer the acentric factor and compare to the experimental value.
c. Plot log Prsat versus Tr–1 for the Peng-Robinson EOS and the Peng-Robinson hydrogen bonding EOS, and experiment.
19.20. Acetic acid has a much stronger tendency to dimerize than any alcohol. Therefore, it is not reasonable to assume that Ka2 = Ka3 = … for acetic acid. The assumption is reasonable for Ka3 = Ka4 = …, however. We can supplement the theory by adding a single additional equation for the dimerization reaction with an effective equilibrium constant equal to the ratio of the true Ka2 divided by the linear association value. Assume that the linear association is negligible for the saturated vapor at ~300–350 K.
a. Determine the value of Ka2 that matches the saturated vapor compressibility factor in that range. Let NAεHB/R = 4000 K for the dimerization.
b. Determine the values of KAD, b, αc, εHB that match the critical point.
c. Determine the values of KAD, b, αc, εHB that match the vapor pressure at Tr = 0.7 for acetic acid.
19.21. Extend the ESD equation to compounds with more than one bonding segment.
a. Consider ethylene glycol as a compound with both an associating head and tail. Extend the mixture analysis to treat this case with two bonding segments (Nd = 2).
b. Treat water by the same model noting that water is merely a “very short glycol.” Determine the acentric factor of the Peng-Robinson hydrogen bonding EOS with ΔH = 15 kJ/mole.CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply