Practice Problems

P18.1.

a. Compute the freezing point depression for an aqueous solutions that is 3 wt% NaCl.

b. Compute the boiling point elevation for an aqueous solutions that is 3 wt% NaCl.

c. Compute the osmotic pressure for an aqueous solutions that is 3 wt% NaCl.

18.27. Homework Problems

18.1. Calcium chloride is used occasionally as an alternative to sodium chloride for de-icing walkways. It is rumored to maintain puddles even a day or so after all evidence of sodium chloride has disappeared.

a. Compute the freezing point depression for aqueous solutions that are 5 wt% CaCl₂ and NaCl.

b. Compute the boiling point elevation for aqueous solutions that are 5 wt% CaCl₂ and NaCl.

c. Compute the osmotic pressure for aqueous solutions that are 5 wt% CaCl₂ and NaCl.

18.2. Ammonia is a weak base, as indicated by the pK_a,A and pK_a,B values in Table 18.2. Determine the percentage of NH₃ dissociated at pH 7 and pH 1.5 when the apparent amount of NH₃ in aqueous solution is 0.15 m. Assume ideal solutions.

18.3. Sodium fluoride, NaF, is dissolved in water at an apparent concentration of C_B = 10^-3 mol/L. Construct a Sillèn diagram and estimate the pH. Refer to the pK_a,A and pK_a,B values in Table 18.2.

18.4. A solution of NaHCO₃ and HCl is prepared such that the total carbon concentration is 1E-3 M and the total Cl concentration is 2E-3 M. Calculate the pH and concentrations of species present. Assume that the pressure is sufficiently that any evolved CO₂ remains in solution. Estimate the partial pressure of the CO₂ by

a. using Henry’s Law.

a. assuming the MAB model.

18.5. Plot the “apparent molality” of Cl₂ in solution against the partial pressure of Cl₂. The apparent molality is the sum of all Cl species in solution (Cl₂ counts twice) divided by 2 (to put it on a Cl₂ basis). Compare your plot to the experimental data of Whitney and Vivian (1941).³⁹

18.6. Model a soft drink as a solution of water with CO₂ dissolved at 298.15 K. In this way we ignore the sugar, flavor, and color. The Henry’s law constant for CO₂ at 298.15 K is 0.035 (mol/kg-bar).

a. What pH and composition exist when the vapor phase is 3.5 bar absolute at room temperature ignoring O₂ or N₂ present? This approximates conditions in the unopened container.

b. After the soft drink is opened, and the liquid equilibrates with atmosphere, what pH and composition exist when the CO₂ vapor mole fraction is y_CO2 = 0.0003 (the normal ambient value) and the pressure is 1 bar?

18.7. Sodium bicarbonate, NaHCO₃, commonly known as baking soda, is dissolved in water at 10^–2 m at 298.15 K. Assume ideal solutions.

a. Determine the pH and the dominant species concentrations. For this part of the problem, ignore the potential loss of CO₂ escaping from the solution as vapor.

b. Now evaluate whether CO₂ may have a propensity to come out of solution at the conditions determined in (a) at 1 bar total pressure. y_CO2 = 0.0003 is the normal ambient value.

18.8. Sodium carbonate is mixed into a solution of acetic acid and the container is rapidly closed before the container components react. The amount of sodium carbonate is such that the total sodium concentration is 1E-2 m and the total acetate concentration is also 1E-2 m. When the mixture equilibrates, the partial pressure of CO₂ over the solution is measured to be 0.5 bar. Determine the pH and concentrations of the acetate species. The Henry’s law constant for CO₂ at 298.15 K is 0.035 (mol/kg-bar).

18.9. Thermodynamic data for Gibbs energy of formation is shown below (kJ/mol for molal standard states) at 298.15 K. A saturated solution of NaCl is approximately an ideal solution.

a. Use the Gibbs energy of formation to determine the solubility of NaCl in molality at 298.15 K. Treat the equilibrium between the solids and ions as a K_sp.

b. Determine the NaCl solubility (molal) when the concentration of KCl is 1 m.

c. Prove that the solution in part (b) is not saturated with KCl. (An ideal solution is actually a poor approximation for a saturated solution of KCl, but provide the proof based on an ideal solution.)

18.10. Suppose 0.1 mol of CO₂ were mixed with 0.9 mol of Cl₂ and 1 liter of water. What would be the concentrations of the aqueous species and the mole fractions in the vapor phase at 0.8 atm in that case?

18.11. Corrosion resistant alloys (such as nickel alloys and stainless steels) can be susceptible to crevice corrosion in solutions where no corrosion is observed in the bulk solution. For example, nickel base alloys are immune to corrosion in seawater; however, in areas where two pieces of this alloy are joined (typically by a flange and an o-ring) crevice corrosion may be observed. This phenomenon occurs as the result of two conditions, restricted mass transport and water hydrolysis which both act to make the solution inside a crevice more aggressive. Water hydrolysis occurs when metal cations react with water to form acid (H⁺):

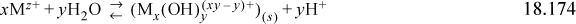
In a bulk solution diffusion, convection and migration transport the acid away from the surface and no damaging effects are observed. However, the restricted mass transport inside a crevice results in accumulation of metal ions under the crevice former and acidification. As a result, the alloy can be exposed to a very aggressive environment. The pH inside the crevice can be calculated from knowledge of empirically determined concentration quotients (Q_xy) where:

You will note that Q_xy is similar to K_a in form; however, here we use concentrations and not activities. Q_xy is another way to express K = K_a/K_γ as given in then end of Section 18.8. As a practical example of this phenomenon, consider austenitic stainless steels which are generally composed of Fe, Ni, and Cr. Corrosion results in the formation of metal cations in solution, the most aggressive cation for stainless steel being Cr⁺³.

a. Given that log(Q₁₃) = –4.6 for Cr⁺³ at a temperature and ionic strength of interest, write the hydrolysis reaction (Eqn. 18.174). Then, solve the corresponding concentration quotient (Eqn. 18.175) to obtain a relation between pH and the concentration of [Cr⁺³].

b. Make a table of the crevice concentrations that result in pH = {6, 4, 2}.

c. Explain why the concentration of  does not appear in Eqn. 18.175.

d. For Fe²⁺, log Q₁₂ = –9.5, and for Ni²⁺, logQ₁₂ = –10.5. Repeat (a) for each of these ions and compare the crevice concentrations with those in part (b).

18.12. Ruthenium (Ru) is a strong oxidation catalyst for organic compounds typically in the form RuO_4(aq) represented as H₂RuO_5(aq), but it is a stoichiometric catalyst because it is reduced during the oxidation of the organic species. Ru species also undergo redox reactions with water and dissolved oxygen. Assume ideal solutions.

a. Show that RuO_4(s) is not stable in contact with an air saturated solution of water and that it will revert to RuO_2(s), independent of pH. (Hint: Water will not appear explicitly in the final reaction.)

b. Show that the solubility of H₂RuO_5(aq) is independent of pH in an aqueous solution saturated with air at 1 bar in contact with RuO_2(s). Calculate the concentration of H₂RuO_5(aq) that would exist at equilibrium.

c. Consider the equilibrium of RuO₄^–_(aq) and H₂RuO_5(aq) in the presence of RuO_2(s). Determine the coefficients for the equation .

d. Consider the equilibrium of RuO₄^–_(aq) and RuO₄^2–_(aq) in the presence of RuO_2(s). Determine the coefficients for the equation .

18.13.

a. Rank the following molecules in order of increasing oxidation of carbon and give the oxidation state of C for each: CO2, -COH(aldehyde), -COOH(carboxylic acid), -CO(ketone), -COH(alcohol), -CH2-, -CH3, CH4.

b. Rank the following C5 molecules in order of decreasing degree of reduction, pentane, valeric acid, 2-pentanone, propyl-ethyl ether, 1-pentanol, 2-methyl butanol, and 1-pentanal.

18.14. The human body processes ethanol by oxidizing it to acetaldehyde via the NAD_ox/NAD_red dehydrogenase redox reaction. The reaction is

NAD_ox + ethanol  NAD_red + acetaldehyde

The values for properties in the order the species appear in the reaction are

ΔG′^o_{f, 310.15}(pH_c =7.4, I=0.25) ={1163.9, 91.45, 1231.0, 43.2}kJ/mol
ΔH′^o_{f, 310.15}(pH_c =7.4, I=0.25) ={–11.9, –291.2, –42.9, –214.1}kJ/mol

a. Determine the magnitude of the heat of reaction under the stated conditions.

b. Calculate the equilibrium constant. If we assume the ratio of the two forms of NAD are near unity, what is implied about the ratio of acetaldehyde:ethanol? What is the importance of sign of the Gibbs energy for the subsequent oxidation of acetaldehyde to acetic acid?⁴⁰

18.15. The first step in biological glycolysis (the catabolic reaction for glucose consumption) involves addition of a phosphate to create glucose 6-phosphate^2–. If the reaction were to occur in aqueous solution “chemically” (as compared to “biochemically’”), it would be written

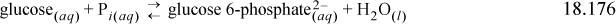
However, in a biological solution, ATP and ADP are carriers of phosphate. Another reaction in solution is the hydrolysis of ATP to ADP:

The transformed values of the Gibbs energies of formation and enthalpy of formation (kJ/mol) at 298.15K, pH_c 7.0, I 0.25m, pMg 3.0 are tabulated below along with the physiological concentrations.

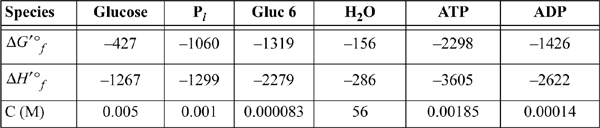
a. Evaluate the standard state Gibbs energy and enthalpy for Eqn. 18.176 and ΔG′ under the actual concentrations.

b. Repeat part (a) for Eqn. 18.177.

c. Biological glycolysis works by coupling the two reactions. Write the overall reaction and evaluate ΔG′ under physiological conditions.

18.16. When we discussed H₃PO₄ in Section 18.9, we developed a recurring relation for the dissociation in Eqn. 18.50. Later we gave with verbal argument a binding polynomial in Eqn. 18.90.

a. Write the series of binding reactions for PO₄^3– and derive the Eqn. 18.50.

b. Create a plot of <i> vs. pH for PO₄^3–.

18.17. Write a binding polynomial for CO₂ in aqueous systems and determine the transformed standard state Gibbs energy of total CO₂ at pH_c = 7 and I = 0.25 m. Give the distribution of aqueous species at these conditions.

18.18.

a. Write the binding polynomial for ATP at 298.15K in terms of binding constants in the absence of Mg for application between 3 < pH_c < 14. Assume ideal solutions. Hint: Use untransformed equilibrium constants calculated from the Gibbs energies of formation, and ignore the species that don’t have Gibbs energies tabulated in the appendix.

b. Convert the binding constants to dissociation constants and give the pK_a,A for each dissociation constant.

c. Using the binding constants, calculate and plot the <i> vs. pH for ATP between 3 < pH_c < 14. Mark the <i> at the pK_a,A values determined in (b).

d. Give the fraction of each species at a pH_c = 7.6.

18.19. Repeat problem 18.18, but use ADP.

18.20. Beginning with the untransformed Gibbs energies of formation, document the intermediate calculations for the value of apparent Gibbs energy of formation of ADP at the conditions of Example 18.10, using the extended Debye-Hückel activity coefficient model and transformed Gibbs energies. Also calculate the distribution of each species.

18.21. Repeat problem 18.20, but use H₃PO₄.

18.22. At pH_c = 7, I = 0.25, beginning with the untransformed Gibbs energies of formation, document the intermediate calculations for the value of apparent Gibbs energy of formation of CO₂ at the conditions using the extended Debye-Hückel activity coefficient model and transformed Gibbs energies. Also calculate the distribution of each species.CopycopyHighlighthighlightAdd NotenoteGet Linklink