P14.1. It has been suggested that the phase diagram of the hexane + furfural system can be adequately represented by the Margules one-parameter equation, where ln γi = xj2 · 800/T (K). Estimate the liquid-liquid mutual solubilities of each component in each liquid phase at 298 K. (ANS. ~10% each, by symmetry)
P14.2. Suppose the solubility of water in ethyl benzene was measured by Karl-Fisher analysis to be 1 mol%. Use UNIFAC to estimate the solubility of ethylbenzene in the water phase. (ANS. 0.003wt% or 30ppmw)
P14.3. According to Perry’s Handbook, the system water + isobutanol forms an atmospheric pressure azeotrope at 67.14 mol% water and 89.92°C. Based on these data, we can estimate the van Laar coefficients to be A12 = 1.566; A21 = 3.833 at 273 K. Estimate the liquid-liquid mutual solubilities of each component in each liquid phase at 273 K. (ANS. 0.33,0.97)
P14.4. Use the SSCED model to predict the solubility of iodine in carbon tetrachloride at 298 K. Iodine’s melting point is 387 K and Hfus = 15.5 kJ/mol.
14.13. Homework Problems
14.1. Suppose the (1) + (2) system exhibits liquid-liquid immiscibility. Suppose we are at a state where G1/RT = 0.1 and G2/RT = 0.3. The Gibbs energy of mixing quantifies the Gibbs energy of the mixture relative to the Gibbs energies of the pure components. Suppose the excess Gibbs energy for the (1) + (2) mixture is given by:
GE/RT = 2.5 x1 x2
a. Combine this with the Gibbs energy for ideal mixing to calculate the Gibbs energy of mixing across the composition range and plot the results against x1 to illustrate that the system exhibits immiscibility.
b. Draw a tangent to the humps to illustrate that the system is one phase at compositions greater than z1 = 0.854 and less than z1 = 0.145, but will split into two phases with compositions at any intermediate overall composition. Most systems with liquid-liquid immiscibility must be modeled with a more complex formula for excess Gibbs energy. The humps on the diagram are usually off-center, as in Fig. 14.3 on page 545 in the text. The simple model used for the calculations here results in the symmetrical diagram.
c. When a mixture splits into two phases, the over-all fractions (of total moles) of the two phases are found by the lever rule along the composition coordinate. Suppose 0.6 mol of (1) and 0.4 mol of (2) are mixed. Use the lever rule to calculate the total number of moles which would be found in each phase of the actual system. Designate the (1)-rich phase as the β phase.
d. What is the value of the hypothetical Gibbs energy, (expressed as G/RT), of a mixture of 0.6 mol of (1) and 0.4 mol of (2) if the mixture were to remain as one phase? Calculate the Gibbs energy of the total system considering the phase split into two phases, and show that the Gibbs energy is less than the Gibbs energy of the single-phase system.
14.2. Assume solvents A and B are virtually insoluble in each other. Component C is soluble in both.
a. Use the Scatchard-Hildebrand theory to estimate the distribution coefficient at low concentrations of C given as (mole fraction C in A)/(mole fraction C in B).
b. If the phase containing A is 0.1 mol% C, estimate the composition of the phase containing B.
c. If an extractor was designed and constructed, is the distribution coefficient favorable for extraction from B into A? Data:
14.3. A new drug is to have the formula para-CH3CH2-(C6H4)-CH2CH2COOH, where (C6H4) designates a phenyl ring. A useful method for assessing the extent of partitioning between the bloodstream and body fat is to determine the infinite dilution partitioning coefficient for the drug between water and n-octanol. Use UNIFAC to make this determination. The body temperature is 37°C. Will the new drug stay in the bloodstream or move into fatty body parts?
14.4. Use the Scatchard-Hildebrand theory to generate figures of activity as a function of composition and ΔGmix as a function of composition for neopentane and dichloromethane at 0°C. Determine the compositions of the two phases in equilibrium. Data:
14.5. The bubble point of a liquid mixture of n-butanol and water containing 4 mol% butanol is 92.7°C at 1 bar. At 92.7°C the vapor pressure of pure water is 0.784 bar and that of pure n-butanol is 0.427 bar. Assuming the activity coefficient of water in the 4% butanol solution is near unity, estimate the composition of the vapor and activity coefficient of butanol that gives the correct bubble pressure and compare to the values estimated by UNIFAC.
14.6. Schulte et al.8 discuss a linear solvation energy relationship (LSER) method for the partitioning of 41 environmentally important compounds between hexane + water phases at 25°C. The LSER method is based on the idea that contributions to the Gibbs excess energy (and to the logarithm of the partition coefficient) from effects like van der Waals forces and hydrogen bonding are independent of each other. Therefore, these contributions can be added up as separate linear contributions. We can test this hypothesis by plotting partition data for several compounds based on experimental data and LSER. We can also test the predictive capabilities of alternative theories by plotting their results with different curves. Table 14.2 presents the required parameters for the LSER method for several compounds. These parameters are to be substituted into the equation:
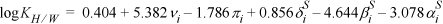
Table 14.2. LSER Parameters and Experimental Hexane + Water Partition Coefficients for Several Compounds
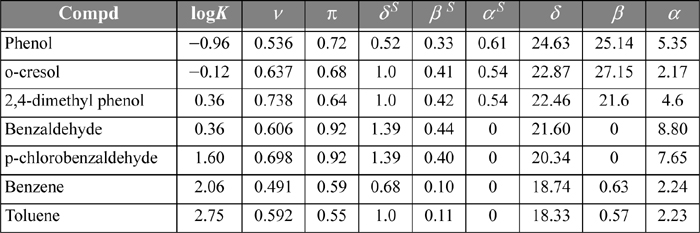
where v = volume parameter, π = polarity parameter, δS = polarizability parameter, βS = hydrogen bond acceptor parameter, and αS = hydrogen bond donor parameter. Compute the log partition coefficients for the following compounds by the LSER method and plot them against the experimental values listed in Table 14.2. Include predictions using the following methods. (Hint: compounds in the environment usually exist at ppm concentrations.)
a. the MAB model.
b. the SSCED model.
c. the UNIFAC model.
14.7. Predict the compositions of the coexisting liquid phases for the system methanol (1) + cyclohexane (2) at 298 K. Let α be the methanol-rich phase.
a. Use the MAB model.
b. Use the SSCED model.
c. Use the UNIFAC model.
14.8. Predict the compositions of the coexisting liquid phases for the system methanol (1) + cyclohexane (2) at 285.15 K and 310.15 K. Let α be the methanol-rich phase. Compare quickly with the data from Fig. 19.12 on page 804 and comment on the accuracy of the results. (Include a printout of your results including converged compositions and activity coefficients of both phases at one of the temperatures.)
a. Use the MAB model.
b. Use the SSCED model.
c. Use the UNIFAC model.
14.9. Benzene and water are virtually immiscible. What is the bubble pressure of an overall mixture that is 50 mol% of each at 75°C?
14.10. Water + hexane and water + benzene are immiscible pairs.
a. The binary system water + benzene boils at 69.4°C and 760 mmHg. What is the activity coefficient of benzene in water if the solubility at this point is xB = 1.6E–4, using only this information and the Antoine coefficients?
b. What is the vapor composition at the bubble pressure at room temperature (292 K) for a ternary mixture consisting of 1 mole overall of each component if the organic layer is assumed to be an ideal solution?
c. What is the vapor composition at the bubble pressure at room temperature (292 K) for a ternary mixture consisting of 1 mole overall of each component if the activity coefficients of the organic layer are predicted by UNIFAC?
The following problems concern LLE in ternary systems. Experimental data for the systems are listed in Tables 14.3 and 14.4.
Table 14.3. Water(1) + Methylethylketone(MEK)(2) + Acetic Acid(3) System at T = 299.85 Ka
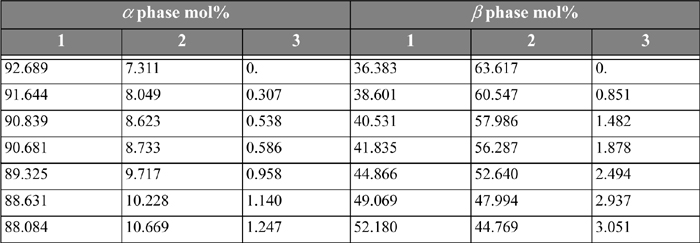
a. Skrzec, A.E., Murphy, N.F. 1954. Ind. Eng. Chem. 46:2245.
Table 14.4. 1-Butanol(1) + water(2) + methanol(3) at 288.15 Ka as reported by Mueller
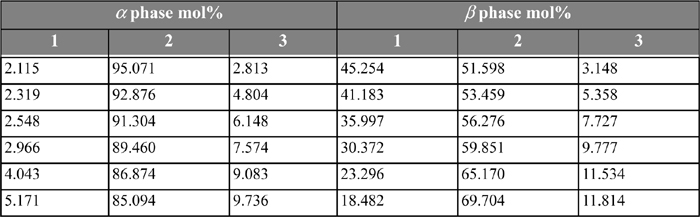
a. Mueller, A.J., Pugsley, L.I., Ferguson, J.B. 1931. J. Phys. Chem. 35:1314.
14.11. Consider the system water(1) + MEK(2) at 299.85 K. The solubilities measured by Skrzec, A.E., Murphy, N.F., 1954. Ind. Eng. Chem., 46:2245, are 
and 
. For a binary system, the LLE iteration procedure has been outlined in Example 14.4. Apply the procedure to determine the mutual solubilities predicted by UNIQUAC. The mixture parameters are r = [0.92, 3.2479], q = [1.40, 2.876], a12 = –2.0882 K, and a21 = 345.53 K. Let phase α be the water-rich phase.
14.12. For a binary system, iterations can be performed by finding a new value of 
from only the K-ratios as shown in Eqn. 14.5. For a ternary system, we need at least one composition. Derive the iteration formula, using 
as the specified composition
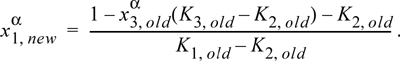
14.13. Consider the system water(1) + methylethylketone(MEK)(2) + acetic acid(AA)(3) at 299.85 K. For a ternary LLE system, estimate tie lines at x3α = 0.005, 0.01, 0.02, using UNIQUAC, where the parameter values are r = [0.92, 3.2479, 2.2024], q = [1.40, 2.876, 2.072], and the a values (in K) are a12 = –2.0882, a21 = 345.53, a13 = 254.15, a31 = –301.02, a23 = –254.13, a32 = –4.5537. Let α be the water-rich phase. Plot the results on rectangular coordinates, using x1 as the abscissa and x3 as the ordinate. Connect the tie lines on the plot. Add the experimental tie lines (Table 14.3) to the same plot using different symbols.
14.14. One mole of a stream containing pentane, acetone, methanol, and water in proportions z = 0.75, 0.13, 0.11, 0.01, respectively, is to be mixed and decanted with 1 mol of pure water at 25°C. Estimate the partition coefficients for each of the components and the proportion of lower-phase/Feed where “Feed” includes both the pentane-rich and pure water streams with the specified model.
a. The MAB model.
b. The SSCED model.
c. The UNIFAC model.
14.15. Calculate the LLE in the system 1-butanol(1) + water(2) + methanol(3) at 288.15 K, using UNIQUAC with the following parameters: r = [3.4543, 0.92, 1.4311]; q = [3.052, 1.4, 1.432]; and the a values (in K) are a13 = 355.54; a31 = –164.09; a12 = –82.688; a21 = 443.56; a32 = –85.451; a23 = –321.92; and compare graphically with the data from Table 14.4.
14.16. Solve problem 14.13, except use the specified model.
a. The MAB model.
b. The SSCED model.
c. The UNIFAC model.
14.17. Consider the system water(1) + methylethylketone(MEK)(2) + propanoic acid(PA)(3). Use UNIFAC to predict the compositions for the coexisting phases at x3α = 0.01, 0.05, and 0.10 at 298.15 K. Let α be the water-rich phase. Plot the results on rectangular coordinates by using x1 as the abscissa and x3 as the ordinate. Connect the tie lines on the plot.
14.18. Solve problem 14.15, except use the specified model.
a. The MAB model.
b. The SSCED model.
c. The UNIFAC model.
14.19. Derive the formulas for the spinodal curves of the Flory-Huggins model and plot the spinodals (T versus xα, xβ) of several polystyrenes in cyclohexane using UNIFAC parameters to estimate the volume of polystyrene relative to ethylbenzene and taking the experimental values of solubility parameters and molar volumes for the species when Nd = 1. Take the degrees of polymerization of polystyrene to be 100, 200, 500, 1000. Plot the estimated reciprocal critical temperatures versus Nd–1/2. Mark the infinite molecular weight critical temperature on both plots with a big X.
Solid-Liquid Behavior
14.20. In the treatment of solid-liquid equilibria, the effects of pressure on melting points are neglected.
a. Draw a schematic of the Gibbs energy of liquid and solid phases versus pressure at constant temperature for a compound for which the molar volume of the solid is less than the molar volume of the liquid. Plot both curves on the same figure, and indicate the melting pressure. Most chemicals follow this type of behavior.
b. For water, the molar volume of the solid is greater than the molar volume of the liquid. Sketch the Gibbs energy of liquid and solid phases as a function of pressure at constant temperature for this type of behavior. Plot both curves on the same figure, and indicate the melting pressure.
c. Calculate the hypothetical Gibbs energy for melting solid naphthalene at 5 bar and the normal melting temperature, 80.2°C. You may assume that the liquid and solid are incompressible. Be sure to clearly specify the path you use for your calculation. VL = 124.8 cm3/gmole, VS = 133 cm3/gmole.
d. Calculate the hypothetical Gibbs energy for melting solid naphthalene at 1 atm and 78°C. Compare the magnitude with the results of part (c) to verify that the pressure effects are small relative to temperature effects.
14.21. Generate a solid-liquid equilibrium T-x diagram for naphthalene(1) + biphenyl(2) assuming ideal solutions. What are the predicted eutectic temperature and composition? The experimental eutectic point is 39.4°C and x biphenyl = 0.555 (Lee, H.H., Warner, J.C., 1935. J. Amer. Chem. Soc. 57:318).
14.22. At 25°C, the solubility of naphthalene in n-hexane is 11.9 mol%. The liquid phase is non-ideal. Use the simple solution model GE/RT = Ax1x2 to predict the solubility at 10°C. (The experimental solubility at 10°C is 6.5mol%, Sunier, A. 1930. J. Phys. Chem. 34:2582).
14.23. Phenanthrene and anthracene are structurally very similar. Would you expect them to have similar solubilities in benzene at 25°C? Provide a quantitative answer, and an explanation.
14.24. Predict the solubility (in mole fraction) of phenol at the cited conditions using the specified model. (i) Use the MAB model. (ii) Use the SSCED model. (iii) Use the UNIFAC model.
a. Solubility in n-heptane at 25°C.
b. Solubility in ethanol at 25°C.
c. Solubility in a 50/50 mole ratio of heptane and ethanol at 25°C.
14.25. A 50 wt% (22.5 mol%) solution of ethylene glycol + water freezes at about 240 K.
a. What freezing temperature would be predicted by assuming that ethylene glycol and water form an ideal solution? The freezing occurs by formation of water crystals.
b. Does your calculation indicate that the system has positive or negative deviations from Raoult’s law? Why?
14.26. Determine the ideal solubility of naphthalene in any solvent at 40°C. Then predict the solubility and compare with the experimental solubility (shown in parentheses) for the specified solvent and specified model. (i) Use the MAB model. (ii) Use the SSCED model. (iii) Use the UNIFAC model.
a. Methanol (4.4)
b. Ethanol (7.3)
c. 1-propanol (9.4)
d. 2-propanol (7.6)
e. 1-butanol (11.6)
f. n-hexane (22.2)
g. Cyclohexanol (22.5)
h. Acetic acid (11.7)
i. Acetone (37.8)
j. Chloroform (47.3)
14.27. Determine the ideal solubility of anthracene in any solvent at 20°C. Then predict the solubility and compare with the experimental solubility (shown in parentheses) for the specified solvent and specified model. (i) Use the MAB model. (ii) Use the SSCED model. (iii) Use the UNIFAC model.
a. Acetone (0.31)
b. Chloroform (0.94)
c. Ethanol (0.05)
d. Methanol (0.02)
14.28. Determine the ideal solubility of phenanthrene in any solvent at 20°C. Then predict the solubility and compare with the experimental solubility (shown in parentheses) for the specified solvent and specified model. (i) Use the MAB model. (ii) Use the SSCED model. (iii) Use the UNIFAC model.
a. Acetone (14.5)
b. Chloroform (23.8)
c. Ethanol (1.23)
d. Acetic acid (1.92)
e. Methanol (0.64)
14.29. Determine the solubility curve for naphthalene in the specified solvent, and compare with the literature data:
a. Acetic acid9
b. n-hexane9
c. Cyclohexanol10
d. Acetone9
e. Chloroform11
f. Methanol9
g. n-butanol9
h. Ethanol12
i. n-propanol12
j. 2-propanol12
14.30. The gas condensate from a new gas well in Prudhoe Bay, Alaska has the following weight% of C5, C10, C15, C20, C25, C30, C35, C40, C45, C50, and >C50, respectively: 1, 4, 7, 10, 12, 12, 12, 12, 8, 8, and 14. Estimate the temperature at which wax may begin to precipitate from this liquid.
14.31. Generate an SLE phase diagram for phenol(1) + cyclohexane(2).
a. Assume an ideal solution.
b. Use MAB to model liquid phase nonidealities.
c. Use SSCED to model liquid phase nonidealities.
d. Use UNIFAC to model liquid phase nonidealities.
e. Make a comment about how the solubility of phenol in cyclohexane differs from the solubility in benzene at the same temperature. (See Fig. 14.12 on page 563.)
14.32. Create a flow sheet analog to VLE or LLE calculations to find the melting temperature and liquid phase composition for a given solid mixture composition for the following.
a. Ideal solutions of solid and liquid
b. Nonideal solutions of solid and liquid
14.33. Create a flow sheet analog to VLE or LLE calculations to find the freezing temperature and solid composition for a given liquid composition when the liquids and solids form a non-ideal solution.
14.34. Create a flowsheet analog to VLE or LLE flash calculations to find the coexisting liquid and solid compositions that exist for a liquid-solid mixture of specified overall composition that is between the conditions of first freezing and first melting.
14.35. Salicylic acid is similar in structure to aspirin. Shalmashi et al.13 have measured the data in Table 14.5.
Table 14.5. Solubility of Salicylic Acid in Various Solvents. Compositions in Weight%
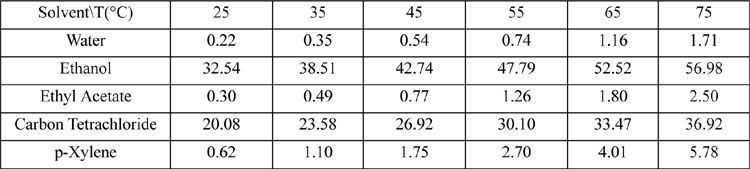
a. Find the value of α for salicylic acid in water that best correlates the data, assuming β = 0.
b. Predict the solubility of the acid in ethanol.
c. Plot log(xacid) versus 1000/T including correlated and measured values.
d. Plot all the calculated versus experimental values. This is known as a parity plot.
14.36. Sometimes we would like to enhance the solubility of a drug by adding a cosolvent, instead of adding antisolvent to precipitate. Making optimal use of the data in the previous problem, estimate the amount of ethanol that should be added to water to prepare an aqueous solution of salicylic acid with concentration of 10 wt% at 25°C.
14.37. Yalkowsky and Rubino (1985)14 have observed roughly linear behavior for logarithmic solubility in mixed solvents when plotted as volume fraction of the solvent/cosolvent. That is, log(xi)= Φ1′log(xi,1) + Φ2′log(xi,2) where xi,j is the solubility in the jth pure solvent and Φi′ is the volume fraction on a solute-free basis; for example, ΦE′ = ΦE/(ΦE + ΦW). Use the SSCED model to make your best estimates of the solubility of salicylic acid at 318 K in a range of mixtures with ethanol/water mole fraction ratios of 3/1, 1/1, and 1/3. Plot your results as log10(xacid) versus ΦE′. Include the experimental results and the guideline of Yalkowsky and Rubino. Comment on whether the SSCED model is consistent with the observation of Yalkowsky and Rubino.CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply