The excess Gibbs energy is
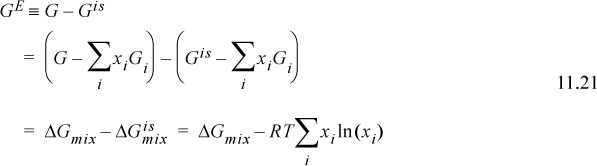
where we have added and subtracted the sum of the component Gibbs energies in the second line, and used Eqns. 10.65 and 10.66 in the last line. Let us further examine ![]() .
.
Recall that ![]() , (Eqn. 10.42). Previously in Eqn. 10.48 we expressed μi relative to a pure component value using a ratio of fugacities. Generalization of this equation will provide the link between Gibbs energies and component fugacities that will lead to the activity coefficient models. If we calculate the chemical potential relative to a standard state, we find by generalizing 10.48
, (Eqn. 10.42). Previously in Eqn. 10.48 we expressed μi relative to a pure component value using a ratio of fugacities. Generalization of this equation will provide the link between Gibbs energies and component fugacities that will lead to the activity coefficient models. If we calculate the chemical potential relative to a standard state, we find by generalizing 10.48

This ratio of fugacities will appear often, and it is convenient to define the ratio as the activity, and it can be related to composition using the activity coefficient,

Using a standard state at the T and P of the system (cf. page 425), ![]() , we can develop an expression for ΔGmix,
, we can develop an expression for ΔGmix,
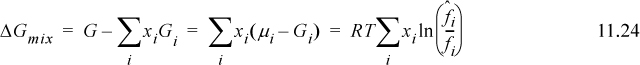
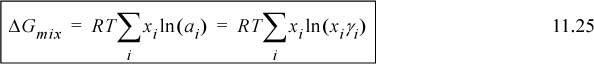
Substituting into Eqn. 11.21:
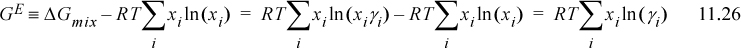

![]() Excess Gibbs energy is zero for an ideal solution, and activity coefficients are unity.
Excess Gibbs energy is zero for an ideal solution, and activity coefficients are unity.
Note that the activity coefficients and excess Gibbs energy are coupled—when the activity coefficients of all components are unity, the excess Gibbs energy goes to zero. The excess Gibbs energy is zero for an ideal solution.
Activity Coefficients as Derivatives
Activity coefficients are related to derivatives of the excess Gibbs energy, specifically the partial molar excess Gibbs energy. We have a very simple relation between partial molar quantities and molar quantities developed in Eqn. 10.41,
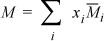
Applying this relation to excess Gibbs energy,
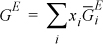
Comparing this with Eqn. 11.27, we see that
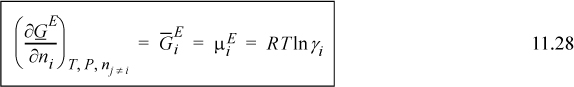
![]() Activity coefficients are related to the partial molar excess Gibbs energy.
Activity coefficients are related to the partial molar excess Gibbs energy.
where we have recognized that the partial molar excess Gibbs energy of a component is also the component excess chemical potential. So, for any expression of GE (T,P,x), we can derive γ’s.
For the one-parameter Margules,
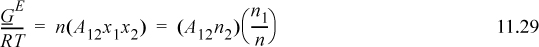
Applying Eqn. 11.28 for i = 1, and using the product rule on n1/n = n1(1/n),
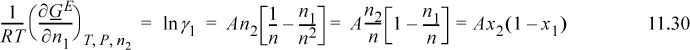
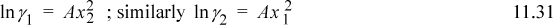
Leave a Reply