We have introduced the concepts of energy of mixing, enthalpy of mixing, and volume of mixing in Section 3.4. We can now relate the mixing behavior to the partial molar properties. The partial molar quantities for ideal gases must be the same as the pure component properties.
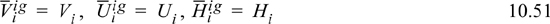
Entropy for an ideal-gas mixture is more complicated because, as shown in Chapter 4, even systems of fixed total energy have an entropy change associated with mixing due to the distinguishability of the components. The entropy of an ideal gas is calculated by the sum of the entropies of the components plus the entropy of mixing as given in Chapter 4:
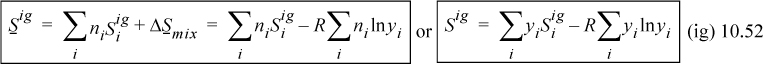
Therefore, the entropy of mixing is nonzero and positive:
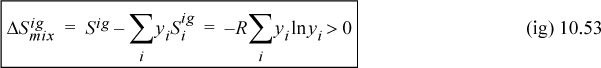
and the partial molar entropy is
The Gibbs energy and the fugacity will be at the core of phase equilibria calculations. The Gibbs energy of an ideal gas is obtained from the definition, G ≡ H – TS. Using Hig an Sig from above,
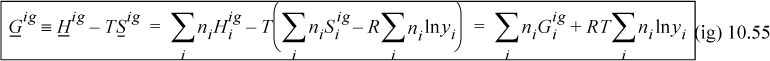
Therefore, the Gibbs energy of mixing is nonzero and negative:
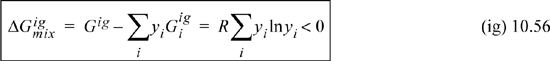
The chemical potential of a component is given by Eqn. 10.39 and taking the derivative of Eqn. 10.55,
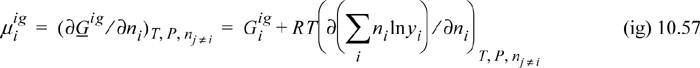
The derivative is most easily seen by expanding the logarithm before differentiation, ln yi = ln ni – ln n. Then,
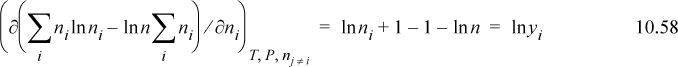
Therefore, we find the chemical potential of an ideal-gas component:
Chemical potential of an ideal-gas component.
By Eqn. 10.48, using Eqn. 10.59 and Eqn. 10.45,
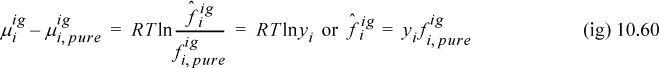
By Eqn. 9.22, 
, resulting in the fugacity of an ideal-gas component:
Therefore, the fugacity of an ideal-gas component is simply its partial pressure, yiP. This makes the ideal-gas fugacity easy to quantify rapidly for engineering purposes. One of the goals of the calculations that will be pursued in Chapter 15 is the quantification of the deviations of the fugacity from ideal-gas values quantified by the component fugacity coefficient.
Leave a Reply