Mixing Rules for Equations of State

Virial Equation of State

The virial equation was introduced for pure fluids in Section 7.4. Previously, we have also given a strategy for relating parameters to composition in Section 12.1. If we extend this mixing rule to the virial equation,

which for a binary mixture becomes

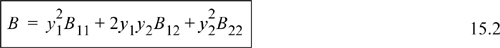
Similar to our previous discussion, it is understood that B₁₂ is equivalent to B₂₁. The cross coefficient B₁₂ is not the virial coefficient for the mixture.

 Combining rules are used to quantify the parameters that represent unlike molecule interactions.

To obtain the cross coefficient, B₁₂, we must create a combining rule to propose how the cross coefficient depends on the properties of the pure components 1 and 2. For the virial coefficient, the relationship between the pair potential and the virial coefficient was given in Section 7.11. However, a less rigorous method is often used in engineering applications. Rather, combining rules are created to use the corresponding state correlations developed for pure components in terms of T_c12 and P_c12. The combining rules used to determine the values of the cross coefficient critical properties are:

 Binary interaction parameters are used to adjust the combining rule to better fit experimental data, if available.

The parameter k′₁₂ is an adjustable parameter (called the binary interaction parameter) to force the combining rules to more accurately represent the cross coefficients found by experiment.¹ However, in the absence of experimental data, it is customary to set k′₁₂ = 0.

and

The first three of these combining rules lead to:

Then, T_c12, P_c12, and ω₁₂ are used in the virial coefficient correlation presented in Chapter 7 to obtain B₁₂ (Eqns. 7.6–7.10) which is subsequently incorporated into the equation for the mixture. If Z_c (or V_c) is not available, it may be estimated using Z_c = 0.291 – 0.08ω. The virial equation for a binary mixture is implemented on the spreadsheet Virialmx.xlsx furnished with the text.

 Virialmx.xlsx.

---

Example 15.1. The virial equation for vapor mixtures

Calculate the molar volume for a 60 mole% mixture of neopentane(1) in CO₂(2) at 310 K and 0.2 MPa.

Solution

The conditions are entered in the spreadsheet Virialmx.xlsx, with the following results:

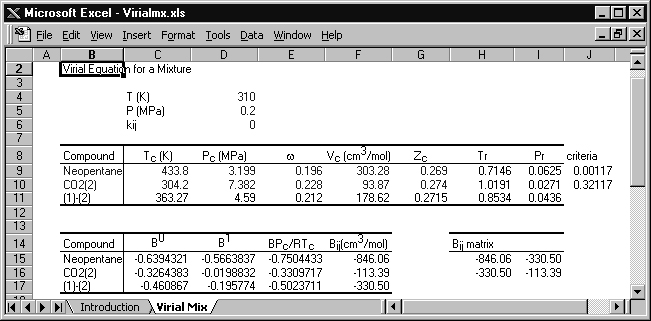
The original spreadsheet is modified slightly for this solution. Cells J9 and J10 are programmed with a rearranged form of Eqn. 7.10, T_r – 0.686 – 0.439P_r, and if these cells are positive, then the virial equation is suitable. The critical volume is calculated from T_c, P_c, and Z_c. Cells F15–F17 list the virial coefficients for neopentane, CO₂, and the cross coefficient, respectively.

The virial coefficient for the mixture is given by Eqn. 15.1,
B = 0.6²·(–846.06) + 2(0.6)(0.4)(–330.5) + 0.4²·(–113.39) = –481.36 cm³/mol
V = RT/P + B = 8.314 · 310/0.2 – 481.36 = 12,405 cm³/mol

The volumetric behavior of the mixture depends on composition. The mixture volume differs from an ideal solution, . The difference V – V^is is called the excess volume, V^E.

The molar volume of pure neopentane is

V = RT/P + B = 8.314 · 310/0.2 – 846.1 = 12,041 cm³/mol

The molar volume of pure CO₂ is

V = RT/P + B = 8.314 · 310/0.2 – 113.4 = 12,773 cm³/mol

The molar volume of an ideal solution of a 60 mole% neopentane mixture is

V^is = 0.6(12,041) + 0.4(12,773) = 12,334 cm³/mol

and the excess volume is

V^E = 12,405 – 12,334 = 71.2 cm³/mol.

The molar volume and excess volume can be determined across the composition range by changing y’s in the formulas.

---

Cubic Equations of State

The customary mixing rules for cubic equations of state have been introduced in Section 12.1:

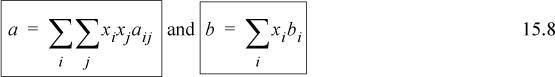
Note the mathematical similarity of the mixing rule for a with the mixing rule used for the virial coefficient. All of the compositional dependence of the equation of state is incorporated into the two relations. A combining rule is not necessary for the b term, however the a term does require a combining rule. The customary combining rule is

where k_ij is referred to as a binary interaction parameter. This is similar to the form of the geometric mean rule for critical temperatures used for virial coefficients. The adjustable parameter k_ij is used to adjust the combining rule to fit experimental data more closely. Technically, this just transfers our ignorance into the adjustable parameter k_ij. Values for k_ij for various binary combinations are tabulated in the literature.²

In the absence of experimental data or literature values for k_ij, we may make a first-order approximation by letting k_ij = 0. This approximation serves our purpose nicely, because the equation of state approach then requires no more information than the ideal solution approach (T_c, P_c, ω, T, P, x, y), but it offers the possibility of more realistic representation of the phase diagram because of the more fundamental molecular basis. We can demonstrate this improved accuracy by considering some examples.

 Review of the concepts from Section 10.8 may help put the approaches in context. Keep in mind that the objective is still to perform bubble, dew and flash calculations, but after relaxing the ideal solution assumption.