Mean Ionic Activity Coefficients

Mean ionic activity coefficients are often used for electrolytes modeling in the literature. The mean ionic activity coefficients provide an alternative method to express the activity of the apparent electrolyte species. This section provides the background to relate those activity coefficients to the ion activity coefficients. The chemical potential of the apparent electrolyte species is the same as the undissociated electrolyte species as shown in Supplement Section 18.23, however only the undissociated chemical potential is used here to keep the equations shorter.

If we insert Eqns. 18.99 and 18.100,

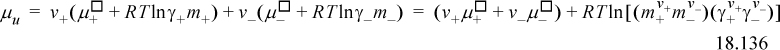
Looking at the last terms in parentheses, we can define,

The molality and activity coefficients are averaged by taking the geometric mean. In the literature, these are commonly called the mean, and the clarification as the geometric mean is commonly omitted. The mean molality is

where v ≡ (v₊ + v_–). The mean ionic activity coefficient is found from the geometric mean of the ion activity coefficients:

This results in the following relation for the chemical potential of the undissociated species

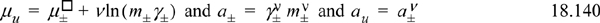
Note that in the formula for chemical potential, the variable v appears before the ln term, unlike the similar expression for ions or nonelectrolyte species. Therefore, the mean ionic activity is not the same as the activity of the undissociated (or apparent) activity. There is no new information in these equations. They are simply an alternative method of expressing the activity coefficients, molalities, and chemical potentials. The mean molal activity coefficient is

The final equation requires a proof that  is related to . To see this, start with the charge balance, v₊z₊ + v_z_ = 0. Obtain one equation by multiplying by z₊ and another by multiplying by z_. Add them and rearrange:

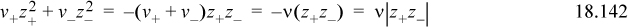
The extended Debye-Hückel model is valid for 1-1 electrolytes up to about 0.1 molal, and to lower concentrations for species with multiple charges: The extended Debye-Hückel is compared with experimental mean ionic activity coefficients for NaCl in Fig. 18.15. Note that the experimental activity coefficients for NaCl are nearly 1 near 6 m. This happens to be about the solubility limit at room temperature, but the solution is quite nonideal at lower concentrations.

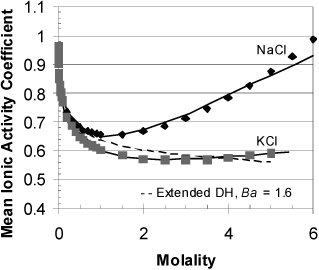
Figure 18.15. Mean ionic activity coefficient for NaCl, KCl and those predicted by the extended Debye-Hückel (DH) model at 298K. Dashed line is the extended Debye-Hückel, Solid lines are the unsymmetric eNRTL using default parameters in ASPEN Plus ver. 7.1. Experimental activity coefficients are from Hamer, W.J.; Wu, Y.-C., 1972. J. Phys. Chem. Ref. Data, 1:1047.

The osmotic pressure can be manipulated using the Gibbs-Duhem equation to obtain the mean ionic activity coefficient. The derivation is beyond the scope intended here, but the equation is

The use of the square root is a necessary mathematical manipulation. The integral may be done numerically. One difficulty is that the experimental data must extend to low concentrations.