When a liquid component is involved in a reaction, the fugacity ratio for activity in Eqn. 17.15 is typically expressed using activity coefficients. Thus,
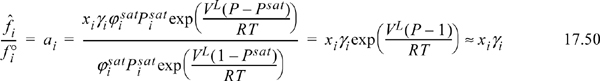
where P is expressed in bar, and the Poynting correction is often negligible, as shown. Another important change in working with liquid components is that in determining Ka liquid phase values are used for 
, not the ideal gas values. Frequently these values are not available in the literature, so it is common to express equilibrium in terms of temperature-dependent correlations for Ka as described in Section 17.18.
Equilibrium constants calculated using liquid phase species are different from the equilibrium constants for the same reactants and products in the gas phase. Consider that 
for the vapor phase. If a vapor phase reaction is simultaneously in phase equilibrium with a liquid phase with the same components, by modified Raoult’s law we could replace 
. However, for the liquid equilibrium constant we should use only the activity (Eqn. 17.50) without the vapor pressure. Thus, we conclude that the equilibrium constants for the liquid phase reaction must be different from the equilibrium constant for the same vapor phase reaction, and also that the standard state Gibbs energy change for the same reaction must be different.
Example 17.10. Oligomerization of lactic acid
Lactic acid is a bio-derived chemical intermediate produced in dilute solution by fermentation. Lactic acid is an α-hydroxy carboxylic acid. As an aqueous solution of lactic acid is concentrated by boiling off water, the carboxylic acid on one molecule reacts with a hydroxyl on another forming a dimer and releasing water. Denoting the “monomer” as L1 and a dimer as L2,
The dimer has a hydroxyl and carboxylic acid that can react further to form trimer L3,
As more water is removed, the chain length grows, forming oligomers. The oligomerization can be represented by a recurring reaction for chain formation. Each liquid phase reaction that adds a lactic acid molecule can be modeled with a universal temperature-independent value of Ka = 0.2023 and the solutions may be considered ideal.a Commercial lactic acid solutions are sold based on the wt% of equivalent lactic acid monomer. So 100 g of 50 wt% solution would be composed of 50 g of lactic acid monomer and 50 g of water that react to form an equilibrium distribution of oligomers. The importance of including modeling of higher oligomers increases as the concentration of lactic acid increases.
a. Determine the mole fractions and wt% of species in a 50 wt% lactic acid solution in water where the distribution is approximated by only reaction 17.51.
b. Repeat the calculations for an 80 wt% lactic acid solution in water where both reactions are necessary to approximate the distribution.
MATLAB Ex17_10.m may be helpful in calculations for this example.
Solution
a. Basis: 100 g total, 50 g of L1 = (50 g)/(90.08 g/mol) = 0.555 mol initially, 50 g = (50 g)/(18.02 g/mol) = 2.775 mol water initially, and 3.330 mol total. The equilibrium relation is Ka = 0.2023 = xL2xH2O/(xL1)2. Since the total number of moles does not change with reaction, it cancels out of the ratio, and we can write 0.2023 = nL2nH2O/(nL1)2. Introducing reaction coordinate,
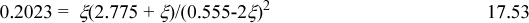
Solving, we find, ξ = 0.0193, xL1 = (0.555 – 2(0.0193))/3.33 = 0.155, xL2 = 0.0193/3.33 = 0.006, xH2O = (2.775 + 0.0193)/3.33 = 0.839. Note that although the mole fraction of L2 seems small, converting to wt%, the water content is (2.775 + 0.0193)(18.02 g/mol)/(100 g)·100% = 50.4 wt%, L1 is (0.555 – 2(0.0193))(90.08 g/mol)/(100 g)·100% = 46.5 wt%, and L2 is 0.0193(162.14 g/mol)/(100 g) · 100% = 3.1 wt%.
b. Basis: 100 g total, 80 g of L1 = (80 g)/(90.08 g/mol) = 0.888 mol initially, 20 g = (20 g)/(18.02 g/mol) = 1.110 mol water initially, and 1.998 mol total. Moles are conserved in both reactions. The equilibrium relations are Ka1 = 0.2023 = xL2xH2O/(xL1)2, Ka2 = 0.2023 = xL3xH2O/(xL2xL1). Introducing the mole numbers and reaction coordinates,
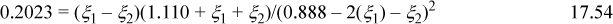
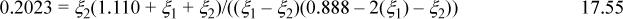
Solving simultaneously, ξ1 = 0.0907, ξ2 = 0.009, xL1 = (0.888 – 2(0.0907) – 0.009)/1.998 = 0.349, xL2 = (0.0907 – 0.009)/1.998 = 0.041, xL3 = 0.009/1.998 = 0.0045, xH2O = (1.110 + 0.0907 + 0.009)/1.998 = 0.6055. The weight fractions are: (1.110 + 0.0907 + 0.009)(18.02 g/mol)/(100 g)·100% = 21.8 wt% water, (0.888 – 2(0.0907) – 0.009)(90.08 g/mol)/(100 g)·100% = 62.8 wt% L1, and (0.0907 – 0.009)(162.14 g/mol)/(100 g)·100% = 13.2 wt% L2, 0.009(234.2 g/mol)/(100 g)·100% = 2.1 wt% L3.
a. Vu, D. T., Kolah, A.K., Asthana, N.S., Peereboom, L., Lira, C.T., Miller, D.J. 2005. “Oligomer distribution in concentrated lactic acid solutions.” Fluid Phase Equil. 236:125–135.
If a vapor state coexists with a liquid phase during a reaction, the phase equilibria and reaction equilibria are coupled. Reactions need to be considered in only one of the two phases, and the equilibrium compositions will be consistent with compositions that would have been determined by the same reaction equilibria in the other phase. Similarly, some reaction equilibria constants may be known for only one or the other of the phases, and the equilibria can be solved by using reaction equilibria for whichever phase is most convenient. Simultaneous reaction and phase equilibria can be extremely useful for driving reactions in preferred directions as we illustrate in Example 17.15.
Leave a Reply