You have probably performed some reaction equilibrium computations before, usually in high school or freshman chemistry. This chapter shows how the “activities” (partial pressures for ideal gases) of products divided by reactants can be related to a quantity, Ka, that does not depend on pressure or composition, and despite its dependence on temperature, it is called the equilibrium constant. Developing the relationship between activities utilizes the concept of minimizing Gibbs energy and rearranging the basic relation. By study of the derivation we learn how to generalize reaction equilibrium analysis to multiple reactions and simultaneous reaction and phase equilibria.
We begin the chapter with an example to provide an overview of some of the methods developed in the chapter. We have selected an introductory reaction where all species are approximated as ideal gases. For ideal gases, we show in upcoming sections that the relation between equilibrium constraint and partial pressure is written

where the symbol Π designates a product (analogous to the symbol ∑ representing the summation sign), yiP is the partial pressure (always expressed in bar) of the ith component, and vi is the stoichiometric coefficient discussed in Section 3.6. Since stoichiometric coefficients are negative for reactants, the product symbol results in a ratio of products over reactants. The solution primarily requires a mass balance relating the partial pressure to the reaction coordinate (also discussed in Section 3.6). The major steps to solving an equilibrium problem are as follows.
1. Ascertain how many phases are present and the method to be used for the equilibrium calculations. Our initial examples will use only a gas phase and determine equilibrium compositions using an equilibrium constant method. Later we will show how to use liquid and solid phases and how to use the Gibbs energy directly.
2. Use standard state properties to obtain the value of the equilibrium constant at the reaction temperature, or for the Gibbs minimization method find the Gibbs energies of the species. Usually this consists of two substeps:
a. Perform a calculation using the standard state Gibbs energies at a reference temperature and pressure.
b. Correct the temperature (and pressure for Gibbs method) to the reaction conditions.
3. Perform a material balance on the reactant and product species and relate the composition to the equilibrium constant or standard state properties from steps (1) and (2).
4. Solve for the equilibrium compositions.
The steps are made clearer by a series of examples. Steps (1) and (2) are lengthy, and the applications are easier to see by first studying steps (3) and (4) as we show in the next example. This example will help to provide motivation for understanding how to use the standard state Gibbs energies in steps (1) and (2).
Example 17.1. Computing the reaction coordinate
CO and H2 are fed to a reactor in a ratio of 2:1 at 500 K and 20 bar, where the equilibrium constant is Ka = 0.00581. (We will illustrate how to calculate Ka in Section 17.7.)
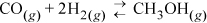
Compute the equilibrium conversion of CO.
Solution
In the expression for Ka we insert each yi P with the appropriate exponent and then insert the numerical value of pressure:
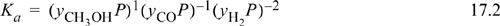
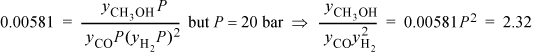
To relate the composition to the mass balance, we select a basis and use the reaction coordinate. Basis: 2 mole CO fed. Note the excess CO at the feed conditions. The reaction coordinate and method of selecting a basis have already been introduced in Section 3.6. The stoichiometry table becomes
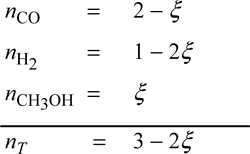
Note that all n values must stay positive, constraining the range for a physically acceptable solution to be 0 ≤ ζ ≤ 0.5. The mole fractions can be written in terms of ζ using the stoichiometry table.
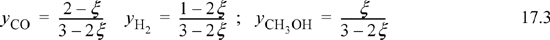
Substituting the mole fractions into the equilibrium constant expression,
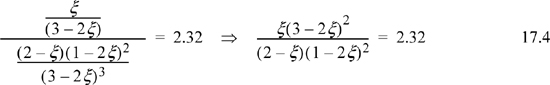
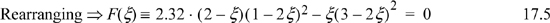
A trial-and-error solution is much more robust by using the difference of Eqn. 17.5 rather than the ratio of Eqn. 17.4. We solve by trial and error and substitute to get ζ recalling 0 ≤ ζ ≤ 0.5. A summary of guesses:
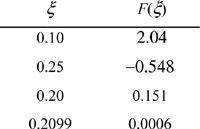
At reaction equilibrium for the given feed conditions, equilibrium is represented by ζ = 0.21. Now Eqn. 17.3 may be used to find the y’s. The conversion of CO is 0.21/2·100% = 10.5%; conversion of H2 is 2(0.21)/1·100% = 42%. Note the conversion is species-dependent with nonstoichiometric feed. Conversion can be increased further by increasing the pressure further, or by changing T where Ka is larger, provided a catalyst is available and kinetics are adequate at that T.
This example demonstrates the method to use Ka to calculate the reaction coordinate. Readers should note that the value of Ka is fixed at a given temperature, but the equilibrium value of ζ may vary for different feed conditions and often pressure for gas phase reactions as we will show in other examples. To relate the equilibrium conditions to reaction engineering textbooks, we note that most reaction engineering textbooks use conversion rather than reaction coordinate to track reaction progress. By convention, conversion is tracked for the limiting species (the species used up first at the value of ζ closest to zero in the direction of the reaction). A relation is shown in the footnote of Section 3.6.
Several other concepts are important for a general understanding of calculating reaction equilibria. First, we must understand: fundamental relations between the Gibbs energies, activities, and the equilibrium constant (Sections 17.2–17.4); simplifications that are applied for ideal gases and the effect of pressure and inerts (Section 17.5); and calculations of the temperature dependence of the equilibrium constants (Sections 17.7–17.9). Later sections illustrate the adaptation of the fundamental equations to broader applications like multiple reactions with simultaneous phase equilibria.
Leave a Reply