Evidence of complexation is often subtle and could be overlooked or ignored in many situations, but its effects are irrefutable in other situations, so a question arises about ignoring facts because they are inconvenient. For example, dimerization of carboxylic acids is observable in the saturated vapor compressibility factor of small acids, but less so for acids of 10 carbons or more. On the other hand, the trend in LCEP discussed in Chapter 16 shows that dimerization is present even in long-chain fatty acids. Another commonly cited example of association is HF vapor, important in petroleum refining and the manufacture of refrigerants, modeled as (HF)n with n predominately 2 or 6. Evidence of this stoichiometry is found in vapor density data. Alcohols are also common substances in the chemical process industry that exhibit association. Spectroscopic data are the best source for characterizing complex formation and further information is available.1 On the other hand, infrared spectra of the hydroxyl stretch, for example, can be difficult to interpret because they include a broad band of stretches indicative of the various oligomers that form in chains. Solid-liquid phase boundaries are indicative of strong complex formation, and may be used to infer complex stoichiometries. For example, the phase diagram for NH3 + water in Fig. 14.14 shows two complexes that form in the solid phase, and might be expected to appear in fluid phases in addition to ionic species. Acetone and chloroform show a 1:1 compound in the solid phase.2 Altogether, the chemical evidence and the results of molecular simulations are converging on the outlook that complexation is an effect that can and should be included in any systematic theory of molecular interactions and phase behavior.
Hydrogen Bonding
Hydrogen bonding is the most common phenomenon leading to association or solvation. As an example, consider the saturated vapor phase compressibility factor of acetic acid. Table 19.1 shows that, even though the pressure is very low for the saturated vapor at low temperature, the vapor compressibility factor of acetic acid deviates considerably from unity, when we would expect the ideal gas law to hold and Z = 1. For comparison, benzene under the same conditions is very nearly an ideal gas.
Table 19.1. P-V-T Evidence of Association from the Compressibility Factors of Saturated Vapors

In the case of acetic acid, the small compressibility factor is due to the dimerization of the carboxylic acid. Even though the pressure is very low, the compressibility factor approaches 0.5 because the number of molecules in the vapor is actually half the apparent amount, owing to the dimerization.3 Note that the compressibility factor increases as the temperature is increased. Why should the conversion to dimer be more complete at low temperature? Because association is an exothermic reaction and the van’t Hoff relation clearly dictates that conversion of exothermic reactions decreases with increasing temperature. Another implication of associating fluids relative to nonassociating fluids is that higher temperatures are needed to make the associating network break into a gas, and this means that Tc for an associating component will be significantly higher than a nonassociating component of similar structure (e.g., H2O versus CH4). The chemical association of acetic acid during dimerization is illustrated in Fig. 19.1. Note that the structure forms two hydrogen bonds simultaneously which makes the dimerization quite strong. Note also that a property of hydrogen bonding is that the O-H-O bond angle is nearly linear. Although the ring has eight atoms, the carboxylic acid structure is close to a six-sided ring, not an eight-sided ring.
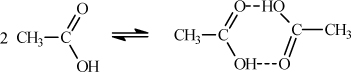
Figure 19.1. Schematic of association in acetic acid.
Hydrogen bonding is also common between different species. For example, the hydroxyl hydrogen in phenol is fairly acidic while trimethyl amine is basic. The trimethyl amine would form a solvation complex in this case, even though it is incapable of association. Hydrogen bonding in solvating systems can enhance miscibility. For example, water and triethylamine are miscible in all proportions below 18°C (and above 0°C where water freezes). However, above 18–19°C, the increased thermal energy breaks the hydrogen bonds resulting in an immiscibility region which increases with increasing temperature4 until the hydrogen bonding energy becomes too weak to influence the phase behavior. To put this into perspective, water miscibility with triethylmethane (aka 3-ethylpentane) is practically negligible at all conditions.
Usually, hydrogen bonding refers to protons bonding when they are attached to O, N, or F. In rare instances, protons bound to carbons can form a complex and it is common to refer to this as hydrogen bonding as well.1 The hydrogen on a highly chlorinated molecule can form a complex with a Lewis base, such as a carbonyl, ether, or amine group. Well-known examples are chloroform + acetone, chloroform + diethyl ether, and acetylene + acetone, as depicted in Fig. 19.2. The chloroform + acetone in homework problem 11.15 should be reconsidered in light of complex formation.
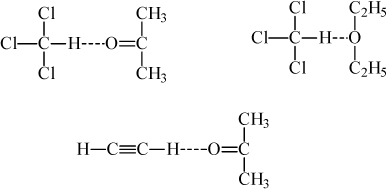
Figure 19.2. Schematic of solvation in several pairs where association of the pure components is negligible.
Charge-Transfer Complexes
Solvation can also occur in the absence of “hydrogen bonding,” per se. Similar kinds of interactions can be called “charge-transfer complexes,” in which case one component is electron-rich (loosely bound electron) and another is strongly electron-attracting (low energy vacant orbital). For example, common electron donors are benzene rings with donating groups like –OH, –OCH3, –N(CH3)2. Common electron acceptors are compounds with several nitro groups (1,3,5-trinitrobenzene), quinones, and compounds with several CN groups (tetracyanoethane, 2,3-dicyano-1,4-benzoquinone). For example, nitrobenzene and mesitylene form a complex when they are mixed as shown in Fig. 19.3. Tetrahydrofuran (THF) and toluene form a charge transfer complex when mixed together. When a charge-transfer complex forms, the energy typically corresponds to about 5 kJ/mole, and the strength is the same order of magnitude as a hydrogen bond. Chemically, these situations are all a bit different, but the mathematics is the same.
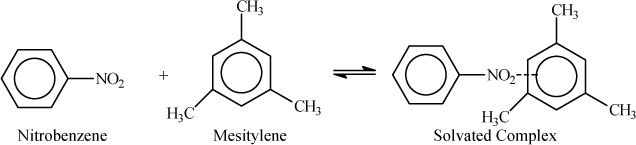
Figure 19.3. Schematic of charge-transfer complexation.
We discussed acidity and basicity in connection with the MOSCED and SSCED models in Chapter 11. Recall that a measure of the relative acidity/basicity is available from spectroscopic measurements tabulated in the Kamlet-Taft acidity/basicity parameters.5 The Kamlet-Taft parameters are determined by comparing spectroscopic behavior of probe molecules in the solvents of interest. A small table of parameters has been included on the back flap.6 These acidity and basicity parameters were designed for the SCED perspective, but they can provide guidelines for the energies of hydrogen bonding and complex formation too. The primary difference is that the SCED perspective does not alter the underlying solution model in a fundamental sense. To clarify, the similarity of the SSCED model to the Scatchard-Hildebrand means that the same solution model would be obtained with proper choices of kij. The kij values of the SSCED model are more predictable, but they do not alter the skewness of the Gibbs excess energy any more than the kij values of the Scatchard-Hildebrand model. Recognizing hydrogen bonding and complexation as mild reactions does alter the skewness of the Gibbs excess energy. In this sense, complexation theory provides an alternative to local composition theory. Whereas local composition theory correlates qualitatively with molecular simulation results, complexation theory correlates quantitatively. This means that a systematic step can be taken in connecting the molecular interactions with their macroscopic behavior.
Preliminary Considerations of Stoichiometry and Notation
In a generalized binary solution,7 the ith complex can be represented by the general form Aai Bbi, where the values of ai and bi are integers which will depend on the particular system (note that for an associated specie, either ai or bi is zero, but that won’t affect the proof). The integers ai and bi are the stoichiometric coefficients:

For example, a hypothetical system is shown in Fig. 19.4 that exhibits both association and solvation where the components A and B are added to the solution in quantities nA and nB.
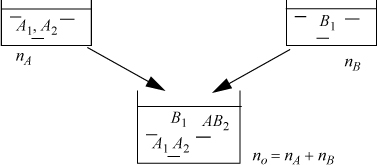
Figure 19.4. Illustration of mixing of species A with species B to form a solution with both association and solvation. The labels in the containers indicate the true species present, not the relative concentrations. The species have been chosen for illustrative purposes.
The concentrations ![]() and
and ![]() are the mole fractions that are experimentally important for macroscopic characterization and are the conventional mole fractions. Since these mole fractions do not represent the true species in solution, they are also called the apparent mole fractions. The mole fractions in the actual solution are called the true mole fractions, and also are denoted by x’s; for example,
are the mole fractions that are experimentally important for macroscopic characterization and are the conventional mole fractions. Since these mole fractions do not represent the true species in solution, they are also called the apparent mole fractions. The mole fractions in the actual solution are called the true mole fractions, and also are denoted by x’s; for example, ![]() ,
, ![]() . Note that xA (the apparent mole fraction) is not the same as (the A monomer mole fraction). Because the monomer mole fraction will end up being so important in later proofs, we give the special subscript M to help distinguish this as the monomer in the true mixture. Therefore, xA1 ≡ xAM, and xB1 ≡ xBM. The true species that are present in solution will usually be inferred from fitting experimental data, and the true mole fractions are usually modeled quantities rather than experimental quantities since they are subject to the assumptions of the model. The nomenclature is nevertheless the established convention in the literature. Note that the implication that the mixture of this discussion is a liquid mixture is not restrictive. The same balances and notation will be used to refer to vapor mixtures, but y’s will be substituted for the x’s.
. Note that xA (the apparent mole fraction) is not the same as (the A monomer mole fraction). Because the monomer mole fraction will end up being so important in later proofs, we give the special subscript M to help distinguish this as the monomer in the true mixture. Therefore, xA1 ≡ xAM, and xB1 ≡ xBM. The true species that are present in solution will usually be inferred from fitting experimental data, and the true mole fractions are usually modeled quantities rather than experimental quantities since they are subject to the assumptions of the model. The nomenclature is nevertheless the established convention in the literature. Note that the implication that the mixture of this discussion is a liquid mixture is not restrictive. The same balances and notation will be used to refer to vapor mixtures, but y’s will be substituted for the x’s.
Leave a Reply