schematically compares a real gas isotherm and an ideal gas isotherm at identical temperatures. At a given {T,P} the volume of the real fluid is V, and the ideal gas volume is Vig = RT/P. Similarly, the ideal gas pressure is not equal to the true pressure when we specify {T,V}. Note that we may characterize the departure from ideal gas behavior in two ways: 1) at the same {T,V}; or 2) at the same {T,P}. We will find it convenient to use both concepts, but we need nomenclature to distinguish between the two departure characterizations. When we refer to the departure of the real fluid property and the same ideal gas property at the same {T,P}, we call it simply the departure function, and use the notation U – Uig. When we compare the departure at the same {T,V} we call it the departure function at fixed T,V, and designate it as (U – Uig)TV.1
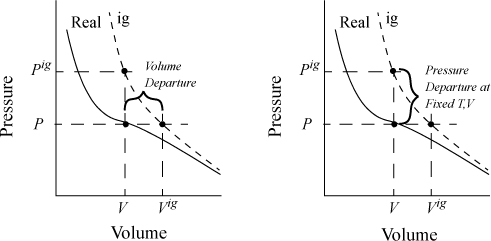
Figure 8.3. Comparison of real fluid and ideal gas isotherms at the same temperature, demonstrating the departure function, and the departure function at fixed T,V.
To calculate the change in internal energy along an isotherm for the real fluid, we write:
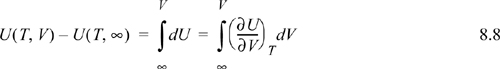
![]() The departure for property M is at fixed T and, P and is given by (M–Mig). The departure at fixed T,V is also useful (particularly in Chapter 15) and is denoted by (M–Mig)TV.
The departure for property M is at fixed T and, P and is given by (M–Mig). The departure at fixed T,V is also useful (particularly in Chapter 15) and is denoted by (M–Mig)TV.
For an ideal gas:
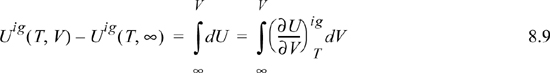
Since the real fluid approaches the ideal gas at infinite volume, we may take the difference in these two equations to find the departure function at fixed T,V,
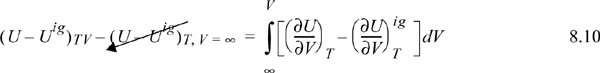
where (U – Uig)T, V = ∞ drops out because the real fluid energy approaches the ideal gas at infinite volume (low pressure). We have obtained a calculation with the real fluid in our desired state (T,P,V); however, we are referencing an ideal gas at the same volume rather than the same pressure. To see the difference, consider methane at 250 K, 10 MPa, and 139 cm3/mole. The volume of the ideal gas should be Vig = 8.314·250/10 = 208 cm3/mole. To obtain the departure function denoted by (U – Uig) (which is referenced to an ideal gas at the same pressure), we must add a correction to change the ideal gas state to match the pressure rather than the volume. Note in Fig. 8.3 that the real state is the same for both departure functions—the difference between the two departure functions has to do with the volume used for the ideal gas part of the calculation. The result is
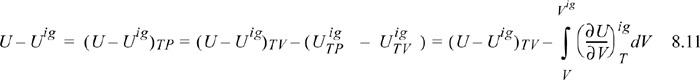
We have already solved for (∂Uig/∂V)T (see Example 6.6 on page 238), and found that it is equal to zero. We are fortunate in this case because the internal energy of an ideal gas does not depend on the volume. When it comes to properties involving entropy, however, the dependency on volume requires careful analysis. Then the systematic treatment developed above is quite valuable.
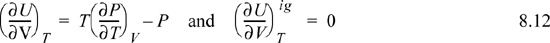
Making these substitutions, we have
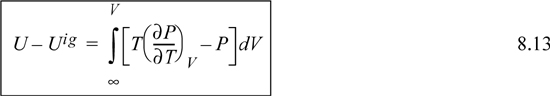
If we transform the integral to density, the resultant expression is easier to integrate for a cubic equation of state. Recognizing dV = –dρ/ρ2, and as V → ∞, ρ → 0, thus,
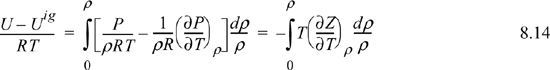
The above equation applies the chain rule in a way that may not be obvious at first:
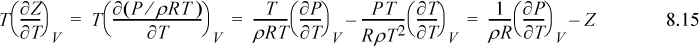
We now have a compact equation to apply to any equation of state. Knowing Z = Z(T, ρ), (e.g., Eqn. 7.15, the Peng-Robinson model), we simply differentiate once, cancel some terms, and integrate. This a perfect sample application of the multivariable calculus that should be familiar at this stage in the curriculum. More importantly, we have developed a systematic approach to solving for any departure function. The steps for a system where Z = Z(T, ρ) are as follows.
1. Write the derivative of the property with respect to volume at constant T. Convert to derivatives of measurable properties using methods from Chapter 6.
2. Write the difference between the derivative real fluid and the derivative ideal gas.
3. Insert integral over dV and limits from infinite volume (where the real fluid and the ideal gas are the same) to the system volume V.
4. Add the necessary correction integral for the ideal gas from V to Vig. (This will be more obvious for entropy.)
5. Transform derivatives to derivatives of Z. Evaluate the derivatives symbolically using the equation of state and integrate analytically.
6. Rearrange in terms of density and compressibility factor to make it more compact.
Some of these steps could have been omitted for the internal energy, because (∂Uig/∂V)T = 0. Steps 1 through 4 are slightly different when Z = Z(T, P) such as with the truncated virial EOS. To see the importance of all the steps, consider the entropy departure function.
Example 8.1. Internal energy departure from the van der Waals equation
Derive the internal energy departure function for the van der Waals equation. Suppose methane is compressed from 200 K and 0.1 MPa to 220 K and 60 MPa. Which is the larger contribution in magnitude to ΔU, the ideal gas contribution or the departure function? Use CP from the back flap and ignore temperature dependence.
Solution
For methane, a = 230030 J-cm3/mol2 and b = 43.07 cm3/mol were calculated by the critical point criteria in Example 7.7 on page 271. Deriving the departure function, –T(dZ/dT)ρ = –aρ/RT, because the repulsive part is constant with respect to T. Substituting,
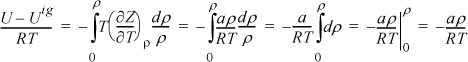
Because Tr > 1 there is only one real root. A quick but crude computation of ρ is to rearrange as Zbρ = bP/RT = bρ/(1 – bρ) – (a/bRT)(bρ)2.
At state 2, 220 K and 60 MPa,
60·43.07/(8.314·220) = bρ/(1 – bρ) – 230030/(43.07·8.314·220)(bρ)2.
Taking an initial guess of bρ = 0.99 and solving iteratively gives bρ = 0.7546, so
(U2 – U2ig)/RT = –230030·0.7546/(43.07·8.314·220) = –2.203.
At state 1, 200 K and 0.1 MPa,
0.1·43.07/(8.314·200) = bρ/(1 – bρ) – 230030/(43.07·8.314·200)(bρ)2.
Taking an initial guess of bρ = 0.99 and solving iteratively gives bρ = 0.00290, so
(U1 – U1ig)/RT = –230030·0.00290/(43.07·8.314·200) = –0.00931.
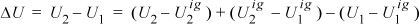
ΔU = –2.203(8.314)220 + (4.3 – 1)·8.314(220 – 200) + 0.00931(8.314)200 = –4030 + 549 + 15 = –3466 J/mol. The ideal gas part (549) is 14% as large in magnitude as the State 2 departure function (–4030) for this calculation. Clearly, State 2 is not an ideal gas.
Note that we do not need to repeat the integral for every new problem. For the van der Waals equation, the formula (U–Uig)/(RT) = –(aρ)/(RT) may readily be used whenever the van der Waals fluid density is known for a given temperature.
Leave a Reply