The simplest method of modeling complex behavior is to neglect the nonidealities by modeling a vapor phase as an ideal gas mixture including the complexes (true fugacity coefficients equal to 1), and to model a liquid phase as an ideal solution containing complexes (true activity coefficients equal to 1). This approach is called Ideal Chemical Theory and can be used to calculate the non-ideal apparent fugacity or activity coefficients. Two brief observations at the outset help to put the chemical perspective into context. First, in reference to systems that can only solvate (not associate), the observed activity coefficients must be less than one because xAM<x°AM when B is present. Second, for systems in which one component associates and the other can neither associate nor solvate, the observed activity coefficients must be greater than one because xAM> x°AM when B is present owing to the interference of B with A from dilution. If you combine these two observations for mixtures that can solvate and associate, you can see how an entire range of activity coefficients may be obtained.
Modeling complex formation with ideal chemical theory, Eqn. 19.3 can be expressed in terms of an equilibrium constant:

Plugging into Eqns. 19.20 and 19.22, the equations to be solved are obtained:
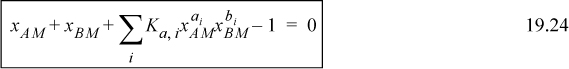
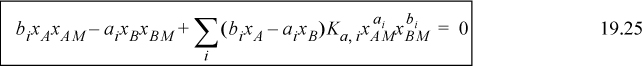
Once the Ki are known, then xAM and xBM can be determined by solving these two equations at a specified apparent concentration. Subsequently, all true mole fractions, xi (Eqn. 19.23) and the apparent mole fractions γA, γB (Eqns. 19.18 and 19.19), can be calculated. If γA, γB are known from experiment, and the complex stoichiometry is known, Ki values can be adjusted to fit the data using optimization methods. A spreadsheet is provided for solving for the true species for given values of Ki in the programs Ichemt.xlsx and Ichemt.m.
For ideal chemical theory applied to the vapor phase, the xi are replaced with yi and Eqn. 19.3 is expressed as

Eqns. 19.20 and 19.22 then become
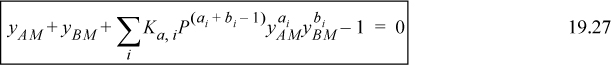
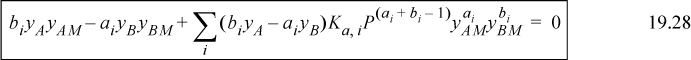
These equations are marked as ideal gas equations since they are ideal gas equations from the perspective of the true solution. As with the liquid-phase calculation, if the Ki values are known, yAM and yBM can be determined.
Example 19.1. Compressibility factors in associating/solvating systems
Derive a formula to relate the true mole fractions to the compressibility factor of a vapor phase where the true species follow the ideal gas law.
Solution
A vessel of volume V holds no apparent moles. However, experimentally, in the same total volume, there would be a smaller number of true moles nT. Applying the ideal gas law,

Experimentally, we wish to work in terms of the apparent number of moles,
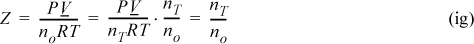
Note that this equation is labelled as an ideal gas equation because the true species follow the ideal gas law, even though from the perspective of the apparent species, the ideal gas law will not be followed. From the total mole balances, ![]() , and
, and ![]() ; therefore,
; therefore,
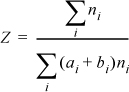
Dividing numerator and denominator by nT,
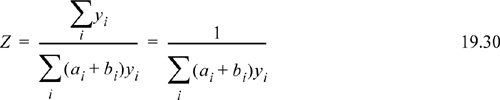
Therefore, once the true mole fractions have been determined, the compressibility factor can be calculated. Determining the true mole fractions requires solving the reaction equilibria, as discussed in the next example.
Example 19.2. Dimerization of carboxylic acids
P-V-T measurements of acetic and propionic acid vapors are available.a The equilibrium constants for acetic and propionic acids at 40°C are 375 bar–1 and 600 bar–1 respectively. At a pressure of 0.01 bar, determine the true mole fractions, the compressibility factor, and the fugacity coefficients.
Solution
Beginning with Eqn. 19.27, letting A be the acid of interest,
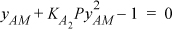
Eqn. 19.28 is not required since the system is a single component. This simple equation can be solved with the quadratic formula,
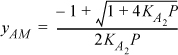
At P = 0.01 bar, for acetic acid, yAM = 0.4, YA2 = 0.6, and even at this low pressure, Eqn. 19.30 gives Z = 0.625. For the fugacity coefficient, starting with Eqn. 19.13,
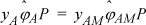
Since the system is pure, yA = 1 and the fugacity coefficient on the left-hand side will be for a pure species. Since the model uses ideal chemical theory, ![]() . Therefore
. Therefore
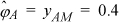
The same procedure can be repeated for propionic acid, however it will be even more nonideal. The answers are: yAM = 0.333, Z = 0.6, ![]() .
.
a. McDougall, F. H., 1936. J. Amer. Chem. Soc. 58:2585; 1941. 63:3420.
Example 19.3. Activity coefficients in a solvated system
1,4-dioxane (component B) is a cyclic 6-member ring, C4H8O2, with oxygens in the 1 and 4 positions. When mixed with chloroform (component A) the oxygens provide solvation sites for the hydrogen on chloroform. Since there are two sites on 1,4-dioxane, two complexes are possible, AB and A2B. McGlashan and Rastogia have studied this system and report the liquid phase can be modeled with ideal chemical theory using KAB = 1.11, KA2B = 1.24 at 50°C. Calculate the true mole fractions and activity coefficients across the composition range.
Solution
We will use the program Ichemt.xlsx to solve Eqns. 15.21 and 15.22. For the A2B compound, ai = 2, bi = 1, Ki = 1.24. For the compositions, we enter increments of 0.05 for the apparent compositions. Near the endpoints, we enter xA = 0.001 and xA = 0.999 to avoid numerical underflows and overflows. The activity coefficients are easily calculated using γA = zA/xA, γB = zB/xB since neither component exhibits association. The results are shown in Fig. 19.5. Note that the solvation causes negative deviation from Raoult’s law. Also note the relation between the complex stoichiometry and the maxima in the complex concentration. Can you rationalize why the infinite dilution activity coefficient of 1,4-dioxane is smaller than the infinite dilution activity coefficient of chloroform?
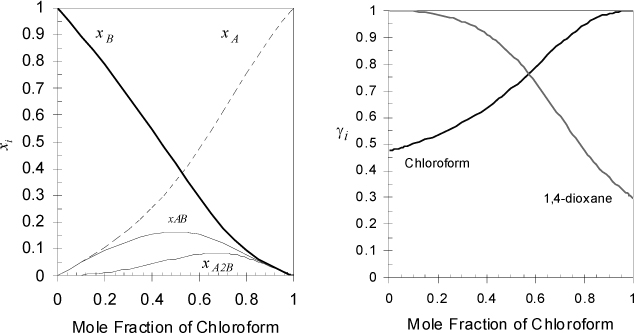
Figure 19.5. Ideal chemical theory applied to the chloroform + 1,4-dioxane system as calculated in Example 19.3.
a. McGlashan, M. L., Rastogi, R. P. 1958. Trans. Faraday Soc. 54:496.
Leave a Reply