17.1. For their homework assignment three students, Julie, John, and Jacob, were working on the formation of ammonia. The feed is a stoichiometric ratio of nitrogen and hydrogen at a particular T and P.
Julie, who thought in round numbers of product, wrote:
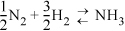
John, who thought in round numbers of nitrogen, wrote:
N2 + 3H2 
2NH3
Jacob, who thought in round numbers of hydrogen, wrote:
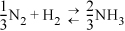
a. How will John’s and Jacob’s standard state Gibbs energy of reactions compare to Julie’s?
b. How will John’s and Jacob’s equilibrium constants be related to Julie’s?
c. How will John’s and Jacob’s equilibrium compositions be related to Julie’s?
d. How will John’s and Jacob’s reaction coordinate values be related to Julie’s?
17.2. The simple statement of the Le Châtelier principle leads one to expect that if the concentration of a reactant were increased, the reaction would proceed so as to consume the added reactant. Nevertheless, consider the gas-phase reaction, N2 + 3H2 2NH3 equilibrated with excess N2 such that N2′s equilibrium mole fraction is 0.55. Does adding more N2 to the equilibrated mixture result in more NH3? Why?
17.3. The production of NO by the direct oxidation of nitrogen occurs naturally in internal combustion engines. This reaction is also used to produce nitric oxide commercially in electric arcs in the Berkeland-Eyde process. If air is used as the feed, compute the equilibrium conversion of oxygen at 1 bar total pressure over the temperature range of 1300–1500°C. Air contains 21 mol% oxygen and 79% N2.
17.4. The following reaction reaches equilibrium at the specified conditions.
C6H5CH = CH2(g) +H2(g) C6H5C2H5(g)
The system initially contains 3 mol H2 for each mole of styrene. Assume ideal gases. For styrene, 
, 
.
a. What is Ka at 600°C?
b. What are the equilibrium mole fractions at 600°C and 1 bar?
c. What are the equilibrium mole fractions at 600°C and 2 bar?
17.5. For the cracking reaction,
C3H8(g) C2H4(g) + CH4(g)
the equilibrium conversion is negligible at room temperature but becomes appreciable at temperatures above 500 K. For a pressure of 1 bar, neglecting any side reactions, determine:
a. The temperature where the conversion is 75%. [Hint: conversion = amount reacted/amount fed. Relate ξ to the conversion.]
b. The fractional conversion which would be obtained at 600 K if the feed to a reactor is 50 mol% propane and 50 mol% nitrogen (inert). (Consider the reaction to proceed to equilibrium.)
17.6. Ethanol can be manufactured by the vapor phase hydration of ethylene according to the reaction: C2H4 + H2O C2H5OH. The feed to a reactor in which the above reaction takes place is a gas mixture containing 25 mol% ethylene and 75 mol% steam.
a. What is the value of the equilibrium constant, Ka, at 125°C and 1 bar?
a. Provide an expression to relate Ka to ξ. Solve for ξ.
17.7. Ethylene is a valuable feedstock for many chemical processes. In future years, when petroleum is not as readily available, ethylene may be produced by dehydration of ethanol. Ethanol may be readily obtained by fermentation of biomass.
a. What percentage of a pure ethanol feed stream will react at 150°C and 1 bar if equilibrium conversion is achieved?
b. If the feed stream is 50 mol% ethanol and 50 mol% N2, what is the maximum conversion of ethanol at 150°C and 1 bar?
17.8. The catalyzed methanol synthesis reaction, CO(g) + 2H2(g) CH3OH(g), is to be conducted by introducing equimolar feed at 200°C. What are the mole fractions and the temperature at the outlet if the system is adiabatic at 10 bar and the catalyst provides equilibrium conversion without any competing reactions?
17.9. A gas stream composed of 15 mol% SO2, 20 mol% O2, and 65 mol% N2 enters a catalytic reactor operating and forms SO3 at 480°C and 2 bar.
a. Determine the equilibrium conversion of SO2.
b. Determine the heat transfer required per mole of reactor feed entering at 295 K and 2 bar.
17.10. The feed gas to a methanol synthesis reactor is composed of 75 mol% H2, 12 mol% CO, 8 mol% CO2, and 5 mol% N2. The system comes to equilibrium at 550 K and 100 bar with respect to the following reactions:
2H2(g) + CO(g) CH3OHg)
H2(g) + Co2(g) CO(g) + H2O(g)
Assuming ideal gases, derive the equations that would be solved simultaneously for ξ1, ξ2 where 1 refers to the first reaction listed. Provide numerical values for the equilibrium constants. Determine ξ1 and ξ2 ignoring any other reactions.
17.11. The 10/25/93 issue of Chemical and Engineering News suggests that the thermodynamic equilibrium in the isomerization of n-butene (CH3CH=CHCH3, a mix of cis and trans isomers) is reached at a temperature of 350°C using a zeolite catalyst. The products are isobutene and 1-butene (CH2=CHCH2CH3). The isobutene is the desired product, for further reaction to MTBE. Determine the equilibrium composition of this product stream at 1 bar.
17.12. Acrylic acid is produced from propylene by the following gas phase reaction:
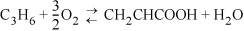
A significant side reaction is the formation of acetic acid:
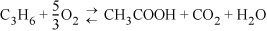
The reactions are carried out at 310°C and 4 bar pressure using a catalyst and air as an oxidant. Steam is added in the ratio 8:1 steam to propylene to stabilize the heat of reaction. If 50% excess air is used (sufficient air so that 50% more oxygen is present than is needed for all the propylene to react by the first reaction), calculate the equilibrium composition of the reactor effluent.
a. As part of a methanol synthesis process similar to problem 17.10, one side reaction that can have an especially unfavorable impact on the catalyst is coke formation. As a first approximation of whether coke (carbon) formation would be significant, estimate the equilibrium extent of coke formation based solely on the reaction: CO + H2 C(s) + H2O. Conditions for the reaction are 600 K and 100 bar.
b. Is coke formation by the reaction from part (a) expected at the conditions cited in problem 17.10?
17.14. Hydrogen gas can be produced by the following reactions between propane and steam in the presence of a nickel catalyst:
C3H8 + 3H2O 3CO + 7H2
CO + H2O CO2 + H2
Neglecting any other competing reactions:
a. Compute the equilibrium constants at 700 K and 750 K.
b. What is the equilibrium composition of the product gas if the inlet to the catalytic reactor is propane and steam in a 1:5 molar ratio at each of the temperatures and 1 bar?
17.15. Write and balance the chemical reaction of carbon monoxide forming solid carbon and carbon dioxide vapor. Determine the equilibrium constant at 700 K and 750 K. Will solid carbon form at the conditions of problem 17.14?
17.16. Catalytic converters on automobiles are designed to minimize the NO and CO emissions derived from the engine exhaust. They generally operate between 400°C and 600°C at 1 bar of pressure. K.C. Taylor (1993. Cat. Rev. Sci. Eng. 35:457.) gives the following compositions (in ppm, molar basis) for typical exhaust from the engine:
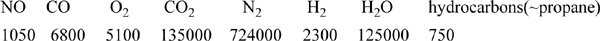
The additional products of the effluent stream include NO2, N2O, N2O4, and NH3. Estimate the compositions of all species at each temperature {400°C, 500°C, 600°C} and plot the ratio of NH3/CO as a function of temperature. (Note: Use the options of the Solver software to set the precision of the results as high as possible.)
17.17. Styrene can be hydrogenated to ethyl benzene at moderate conditions in both the liquid and the gas phases. Calculate the equilibrium compositions in the vapor and liquid phases of hydrogen, styrene, and ethyl benzene at each of the following conditions:
a. 3 bar pressure and 298 K, with a starting mole ratio of hydrogen to styrene of 2:1
b. 3 bar pressure and 423 K, with a starting mole ratio of hydrogen to styrene of 2:1
c. 3 bar pressure and 600 K, with a starting mole ratio of hydrogen to styrene of 2:1
17.18. Habenicht et al. (1995. Ind. Eng. Chem. Res., 34:3784) report on the reaction of t-butyl alcohol (TBA) and ethanol (EtOH) to form ethyltertiary-butyl ether (ETBE). The reaction is conducted at 170oC. A typical feed stream composition (in mole fraction) is:
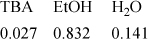
Isobutene is the only significant by-product. Assuming that equilibrium is reached in the outlet stream, estimate the minimum pressure at which the reaction must be conducted in order to maintain everything in the liquid phase. Do isobutene or ETBE exceed their liquid solubility limits at the outlet conditions?
17.19. Limestone (CaCO3) decomposes upon heating to yield quicklime (CaO) and carbon dioxide. At what temperature does limestone exert a decomposition pressure of 1 bar?
17.20. Two-tenths of a gram of CaCO3(s) is placed in a 100 cm3 pressure vessel. The vessel is evacuated of all vapor at 298 K and sealed. The reaction CaCO3(s) = CaO(s) + CO2(g) occurs as the temperature is raised. At what temperature will the conversion of CaCO3 be 50%, and what will the pressure be?
17.21. One suggestion for sequestering CO2 is to synthesize carbonate polymers. Polycarbonate is well known for its strength and transparency. To gauge the feasibility of this approach, consider the synthesis of dimethyl carbonate (DMC) from methanol and CO2 at 350 K.
a. Write a balanced stoichiometric equation for this reaction. Highlight any by-products.
b. Estimate the Ka value for the reaction. What pressure is required to achieve P·Ka = 0.1?
c. Methanol and DMC are both liquids at this temperature. Explain how to estimate their partial pressures at a given extent of conversion. You may neglect the CO2 in the liquid for this question.
17.22. Ethyl acetate is to be produced by a liquid phase reaction.
a. Use the shortcut van’t Hoff equation to calculate the expected conversion of HOAc for equimolar feeds of EtOH and HOAc in a batch reactor at 80°C.
b. Repeat part (a) with a 3:1 ratio of EtOH to HOAc at 80°C.
17.23. Hamilton, et al.,6 have studied the binding of DNA chromosomes to proteins WT1 and EGR1. WT1 uses a zinc binding site to suppress a certain type of kidney tumor. EGR1 binds to regulate cell proliferation. There may be an important regulatory link between the two proteins.7
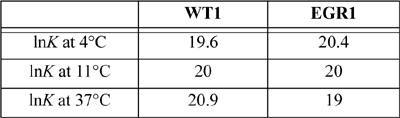
a. Use the binding data above to determine the standard state Gibbs energies of reaction at each temperature, the heat of reaction over the temperature range, and the entropy of reaction over the temperature range.
b. The binding constants are about the same size. Evaluate the relative magnitudes of the enthalpy and entropy of formation for each binding type. Does the thermodynamic analysis imply that the binding types are similar or different?
17.24. The enthalpy of reaction for many biological reactions and surfactants is strongly temperature-dependent, but instead of using full heat capacities, the temperature dependence can be characterized by differences in heat capacities ΔCP = CP,prod – CP,react, typically assumed to be independent of temperature.7
a. The heat of reaction is represented by ΔH = ΔHR + ΔCP(T – TR). Show that
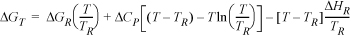
b. Provide an equation consistent with part (a) for the temperature dependence of the entropy of reaction.
17.25. Lysozyme (MW = 14.313 kDa) undergoes a phase transition from a native folded (N) to unfolded state (U) that can be considered a reversible reaction, N(aq) U(aq), where the subscript (aq) indicates that the protein is in an aqueous solution. At high temperature the protein is in state U and at low temperature, it is in state N. The melting temperature (Tm) is where the concentrations are equal. The melting temperature can be changed by pH, ionic strength (added salt), denaturant (solvents), or pressure. The results of problem 17.24 apply. The protein unfolding has been studied by Cooper, et al.8 The heat to unfold 1 mg/mL of protein in 2 mL of pH = 4 solution at Tm = 78°C is 0.0755 J, ΔCP = 6.3 kJ/mol-K. The ΔV = –40 mL/mol.7
a. What is the Gibbs energy change for the unfolding at the melting temperature? (Hint: The answer requires conceptual thought, not many calculations.)
b. Show that at the melting temperature at pH = 4, ΔH = 540 kJ/mol and ΔS = 1.54 kJ/mol.
c. Evaluate the contributions to ΔG at 23°C and pH = 4. Is the process driven by enthalpy or entropy under these conditions?
d. Show that the relation for [N]/[U] is 
For a solution of overall concentration 1 mg/mL, plot [U] as a function of temperature for 20 ≤ T ≤ 110 °C, and provide a tabular summary of [U] at 60°C and 90°C.
e. When pH is varied, the net charges on the protein change (as will be explained in Chapter 18), resulting in different Tm and ΔH. In the range 20 ≤ Tm ≤ 78 °C, the relation is ΔH(kJ/mol) = 48.6 + 6.3 Tm(°C). Derive the relation between ΔS and Tm.
f. At pH = 1, Tm = 43°C. Provide a plot of plot [U] as a function of temperature for 20 ≤ T ≤ 110 °C, and provide a tabular summary of [U] at 25°C and 55°C.
g. (advanced) Lysozyme has four disulfide bonds that are important in the folding behavior. The authors created a mutant protein with only three disulfide bonds. The relation in (e) still holds. At pH = 2.5, Tm = 23°C for the mutant. Evaluate the contributions of enthalpy and entropy to the folding.
h. (advanced) Provide an interpretation for the sign of ΔV. At pH = 4, how much pressure is needed to lower the melting temperature 5°C to 73°C?9
17.26. Surfactants clump together to form organized structures called micelles that can be spheres, rods, and so forth. The formation of the clump can be modeled as a “chemical” reaction, though there are no chemical bonds formed or broken. When surfactants are in solution below the critical micelle concentration, CMC, the surfactant molecules are almost all “free” in solution. At the CMC, micelles start to form. Above the CMC, the amount of free surfactant is almost constant in solution and as more surfactant is added to the solution, more micelles form. It is conventional to provide the property changes of surfactants per mol of surfactant molecules, not per mole of micelle.
a. Given the data below for nonylglucoside (NG) demicellization in water, calculate the micellization value, ΔCPmic, as a function of temperature. Is the heat capacity of a micelle greater than or less than the heat capacity of the molecules that make up the micelle?
b. Calculate ΔSmic and for the surfactant as a function of temperature. Is the overall solution (including water) more ordered or less ordered after micellization?
NG data:
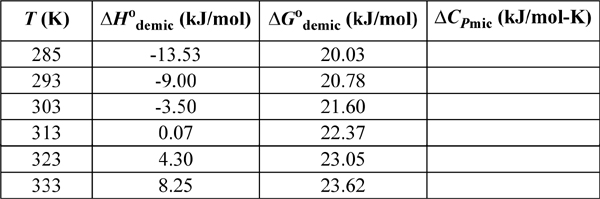
17.27. Micelle formation in surfactants is described in problem 17.26. Solve the problem using the data for sodium docecyl sulfate, SDS in water.
SDS data:
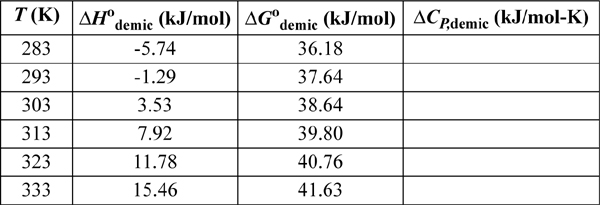
17.28. For nonylglucoside, NG, thermodynamic data for demicellization in water are presented in problem 17.26. Model the micelle reaction as nS Mn where S is free surfactant and Mn is a micelle. Treat the solution as an ideal solution. Vary the total concentration of NG from 0 up to 20 mmol/L. Water is 55.5 mol/L. Calculate mole fractions and molar concentrations (mmol/L) of the free surfactant (in mM) and the micelles (in μM) of NG at T=285 K, where n = 58. Plot curves for the concentrations. Identify the approximate CMC in mmol/L. Hint to simplify calculations: The mol/L added is very small relative water molarity (55.5 mol/L). The density can be assumed to be constant.CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply