13.1. Show that Wilson’s equation reduces to Flory’s equation when Aij = Aji = 0. Further, show that it reduces to an ideal solution if the energy parameters are zero, and the molecules are the same size.
13.2. The actone(1) + chloroform(2) system has an azeotrope at x1 = 0.38, 248 mmHg, and 35.17°C. Fit the Wilson equation, and predict the P-x-y diagram.
13.3. Model the behavior of ethanol(1) + toluene(2) at 55°C using the UNIQUAC equation and the parameters r1 = 2.1055, r2 = 3.9228, q1 = 1.972, q2 = 2.968, a12 = –76.1573 K, and a21 = 438.005 K.
13.4. The UNIFAC and UNIQUAC equations use surface fraction and volume fractions. This problem explores the differences.
a. Calculate the surface area and volume for a cylinder of diameter d = 1.0 and length L = 5 where the units are arbitrary. Calculate the surface area for a sphere of the same volume. Which object has a higher surface area to volume ratio?
b. Calculate the volume fractions and surface area fractions for an equimolar mixture of the cylinders and spheres from part (a). Use subscript s to denote spheres and subscript c to denote cylinders.
c. For this equimolar mixture, calculate the local composition ratios xcs/xss and xsc/xcc for the UNIQUAC equation if the energy variables τcs and τsc are unity. For the equimolar mixture, substitute the values of volume fraction and surface fraction into the expression for UNIQUAC activity coefficients, and simplify as much as possible, leaving the q’s as unknowns.
d. Consider n-pentane and 2,2-dimethyl propane (also known as neopentane). Calculate the UNIQUAC r and q values for each molecule using group contribution methods. Compare the results with part (a). [Hint: You might want to think about the -C-C-C-bond angles.]
13.5. Consider a mixture of isobutene(1) + butane(2). Consider a portion of the calculations that would need to be performed by UNIFAC or UNIQUAC.
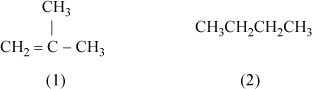
a. Calculate the surface area and volume parameters for each molecule.
b. Provide reasoning to identify which component has a larger liquid molar volume. Which compound has a larger surface area?
c. Calculate the volume fractions for an equimolar mixture.
13.6. Solve problem 10.14 using UNIFAC to model the liquid phase.
13.7. The flash point of liquid mixtures is discussed in Section 10.5. For the following mixtures, estimate the flash point temperature of the following components and their equimolar mixtures using UNIFAC:
a. methanol (LFL = 7.3%) + 2-butanone (LFL = 1.8%)
b. ethanol (LFL = 4.3%) + 2-butanone (LFL = 1.8%).
13.8. Use the UNIFAC model to predict the VLE behavior of the n-pentane(1) + acetone(2) system at 1 bar and compare to the experimental data in problem 11.11.
13.9. According to Gmehling et al. (1994),23 the system acetone + water shows azeotropes at: (1) 2793 mmHg, 95.1 mol% acetone, and 100°C; and (2) 5155 mmHg, 88.4 mol% acetone and 124°C. What azeotropic pressures and compositions does UNIFAC indicate at 100°C and 124°C? Othmer et al. (1946) (cf. Gmehling24) have studied this system at 2570 mmHg. Prepare T-x-y or P-x-y plots comparing the UNIFAC predictions to the experimental data.
13.10. Consider the experimental data of Brown and Smith (1954) cited in problem 10.2. Prepare a P-x-y plot and a plot of experimental activity coefficients vs. composition. Then use UNIFAC to predict the activity coefficients across the composition range and add the calculations to the plots.
13.11. Flash separations are fundamental to any process separation train. A full steady-state process simulation consists largely of many consecutive flash calculations. Use UNIFAC to determine the temperature at which 20 mol% will be vaporized at 760 mmHg of an equimolar mixture liquid feed of n-pentane and acetone.
13.12. A preliminary evaluation of a new process concept has produced a waste stream of the composition given below. It is desired to reduce the waste stream to 10% of its original mass while recovering essentially pure water from the other stream. Since the solution is very dilute, we can use a simple equation known as Henry’s law to represent the system. According to Henry’s law, 
. Use UNIFAC to estimate the Henry’s law constants when UNIFAC parameters are available. Use the Scatchard-Hildebrand theory when UNIFAC parameters are not available. Estimate the relative volatilities (relative to water) of each component. Relative volatilities are defined in problem 11.2.
Compositions in mg/liter are:
13.13. Derive the form of the excess enthalpy predicted by Wilson’s equation assuming that Aij’s and ratios of molar volumes are temperature-independent.
13.14. Orbey and Sandler (1995. Ind. Eng. Chem. Res. 34:4351.) have proposed a correction term to be added to the excess Gibbs energy of mixing given by UNIQUAC. To a reasonable degree of accuracy the new term can be written
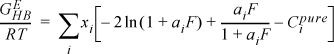
where
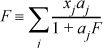
Derive an expression for the correction to the activity coefficient. [Hint: Do you remember how to differentiate implicitly?]
13.15. The energy equation for mixtures can be written for polymers in the form:
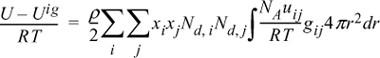
By analogy to the development of the Scatchard-Hildebrand theory, this can be rearranged to:
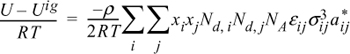
where
Nd,i = degree of polymerization for the ith component
ρ = molar density
xi = mole fraction of the ith component
NA = Avogadro’s number
U = molar internal energy.
aii* = 3 + 2/Ndi
aij* = (aii* ajj*)1/2
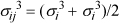
εij = (εii εjj)1/2
Derive an expression for lnγ1 for the activity coefficient model presented above.
13.16. Use the UNIFAC model to predict P–x–y data at 90°C and x1, = {0, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0} for propanoic acid + water. Fit the UNIQUAC model to the predicted P–x–y data and report your UNIQUAC a12 and a21 parameters in kJ/mole.
a. Rearrange Eqn. 13.22 to obtain Eqn. 13.23.
b. Use Eqns. 13.16 and 13.18 in Eqn. 13.17 and perform the integration to obtain Eqn. 13.19.
c. Use Eqns. 13.16 and 13.31 in Eqn. 13.17 and perform the integration to obtain Eqn. 13.40.
13.18. Fit the data from problem 11.11 to the following model by regression over all points, and compare with the experimental data on the same plot, using the
a. Wilson equation
b. NRTL equation
c. UNIQUAC equation
13.19. Work problem 11.25 using the
a. Wilson equation
b. NRTL equation
c. UNIQUAC equation
13.20. Work problem 11.26 using the
a. Wilson equation
b. NRTL equation
c. UNIQUAC equation
13.21. Using the data from problem 11.27, fit the specified model equation and then plot the P–x–y diagram at 80°C using the
a. Wilson equation
b. NRTL equation
c. UNIQUAC equationCopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply