Fugacity and Fugacity Coefficient

In principle, all pure-component, phase-equilibrium problems could be solved using Gibbs energy. Historically, however, an alternative property has been applied in chemical engineering calculations, the fugacity. The fugacity has one advantage over the Gibbs energy in that its application to mixtures is a straightforward extension of its application to pure fluids. It also has some empirical appeal because the fugacity of an ideal gas equals the pressure and the fugacity of a liquid equals the vapor pressure under common conditions, as we will show in Section 9.8. The vapor pressure was the original property used for characterization of phase equilibrium by experimentalists.

The forms of Eqns. 9.16 and 9.15 are similar, and the simplicity of Eqn. 9.16 is appealing. G.N. Lewis defined fugacity by

and comparing to Eqn. 9.16, we see that

 Fugacity and fugacity coefficient are convenient ways to quantify the Gibbs departure.

Integrating from low pressure, at constant temperature, we have for the left-hand side,

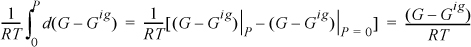
because (G – G^ig) approaches zero at low pressure. Integrating the right-hand side of Eqn. 9.20, we have

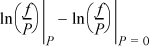
To complete the definition of fugacity, we define the low-pressure limit,

and we define the ratio f/P to be the fugacity coefficient, ϕ.

The fugacity coefficient is simply another way of characterizing the Gibbs departure function at a fixed T,P. For an ideal gas, the fugacity will equal the pressure, and the fugacity coefficient will be unity. For representations of the P-V-T data in the form Z = f(T,P) (like the virial equation of state), the fugacity coefficient is evaluated from an equation of the form:

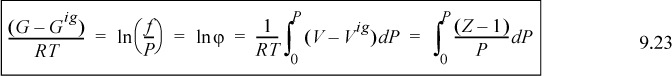
 Fugacity has units of pressure, and the fugacity coefficient is dimensionless.

or the equivalent form for P-V-T data in the form Z = f(T,V), which is essentially Eqn. 8.26,

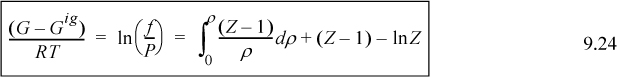
which is the form used for cubic equations of state.

A graphical interpretation of the fugacity coefficient can be seen in Fig. 9.3. The integral of Eqn. 9.23 is represented by the negative value of the shaded region between the real gas isotherm and the ideal gas isotherm. The fugacity coefficient is a measure of non-ideality. Under most common conditions, the fugacity coefficient is less than one. At very high pressures, the fugacity coefficient can become greater than one.

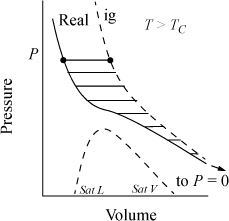
Figure 9.3. Illustration of RT ln ϕ as a departure function.

Note: In practice, we do not evaluate the fugacity of a substance directly. Instead, we evaluate the fugacity coefficient, and then calculate the fugacity by