Flory-Huggins and van der Waals Theories

We have shown that the contribution to the excess internal energy in the Flory-Huggins theory is identical to that in the Scatchard-Hildebrand theory. We derived the Scatchard-Hildebrand theory from the excess internal energy function of the van der Waals equation on page 468 and 12.3 on page 471. Therefore, any potential difference between the Flory-Huggins theory and the van der Waals equation must pertain to the entropy. Reviewing briefly, the van der Waals equation of state gives

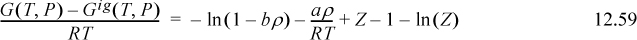
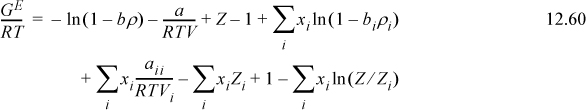
Recall that the van der Waals equation gives .

Therefore, . Comparing  to the result for regular solutions, we see that,

U^E = Φ₁Φ₂(δ₁ – δ₂)²(x₁V₁ + x₂V₂)

which is the same. We may also note that  is a very small number because: 1) These are liquid compressibility factors, so all Z’s are small numerically; and 2) the excess volume is usually a small percentage of the total volume, . Thus, we may neglect .

Turning to the differences between the entropy terms, the van der Waals equation gives

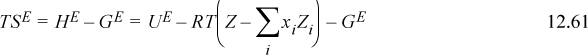
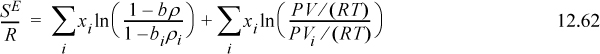
Note: (1 – b_iρi) = (V_i – b_i)/V_i ≡ (V_iϖ)/V_i = ϖ. This means that b_i ρ_i = bρ for all i.

If we assume that ϖ is a universal constant for all fluids, including the mixture, then

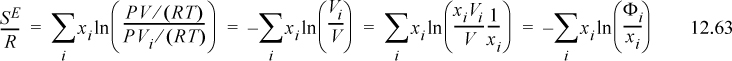
This expression is identical to Flory’s equation (and note the importance of the ln(Z) term as the second term on the right-hand side of Eqn. 12.62, which derived from the ideal gas reference state). Therefore, the only difference between van der Waals’ and Flory’s theories is the assumption that ϖ is a universal constant. This is equivalent to saying that the packing fraction (bρ) is a constant (the packing fraction is one minus the void fraction). In other words, the Flory-Huggins theory is simply the van der Waals theory with the assumption that bρ = constant. The difference between the Flory-Huggins theory and the Scatchard-Hildebrand theory is accounting for mixing at constant pressure instead of mixing at constant packing fraction. This is related to the argument about free volume being larger for larger molecules because fitting a polymer in the same volume as a solvent must lead to a deviation from the ideal gas law at some degree of polymerization. Therefore, the V in PV/RT must be proportional to the volume of the molecule.

The suggestion that bρ = constant is actually quite consistent with another observation that should seem more familiar. That is, the mass density of a polyatomic species is only weakly dependent on its molecular weight. For example, the mass density of decane is 0.73 g/cm³ and the density of n-hexadecane is 0.77 g/cm³. Since the molar density decreases inversely as molecular weight increases but the b-parameter increases proportionally as molecular weight increases, a constant value for the mass density implies a constant value for bρ. When you consider that the mass density for almost all hydrocarbons, alcohols, amides, amines, and their polymers lies between 0.7 and 1.3 g/cm³, you begin to get an idea of how broadly applicable this approximation is.

Nevertheless, there are some obvious limitations to the assumption of a constant packing fraction. A little calculation would make it clear that the ϖ for liquid propane at T_r = 0.99 is significantly larger that ϖ for toluene at T_r = 0.619. Thus, a mixture of propane and toluene at 366 K would not be very accurately represented by the Flory-Huggins theory. Note that deviations of ϖ from each other are related to differences in the compressibilities of the components. Thus, it is common to refer to the Flory-Huggins theory as an “incompressible” theory and to develop alternative theories to represent “compressible” polymer mixtures. Not surprisingly, these alternative theories closely resemble the van der Waals equation (with a slightly modified temperature dependence of the a parameter). This observation lends added significance to Rayleigh’s statement: “I am more than ever an admirer of van der Waals.”