Fitting the Constants for an Associating Equation of State

To this point in the discussion, we have assumed that the constants needed for a fluid are available. However, association models add complexity in the sense that two association parameters must be characterized in addition to the usual size (b), energy (a or ε), and shape (k, m, q, or c). One simple approach is to assign standardized values to the bonding volume and energy. For example, alcohols can be assigned an energy of 17 kJ/mol. Aldehydes, amides, amines, and nitriles can be assigned an energy of 5.2 kJ/mol. Given the bonding energy and volume, three parameters remain to be determined in a manner equivalent to three parameter corresponding states.

The simplest case is when the association energy is zero. Then the critical method can be applied in the usual way. For the ESD model, this is especially simple, because it is cubic. The approach of setting (Z–Z_c)³ = 0 can be applied over a range of values of c from 1 to infinity. For each value of c, the acentric factor can be computed once the critical point has been determined. Then the value of c can be regressed as a function of acentric factor, and values of b and ε can be correlated as functions of c. This results in the following correlations,

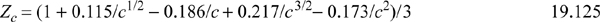
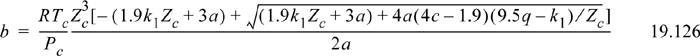
where a = 1.9(9.5q – k₁) + 4ck₁ and k₁ = 1.7745

An interesting implication of this result is that Z_c → ⅓ in the infinite chain limit. Lue et al. showed that this is a general result for all SAFT models, despite the experimental observation that Z_c appears to approach zero for long chains.²⁹ They attributed this deficiency to inaccurate characterization of the intramolecular interactions by SAFT models at low density and high temperature.

At a slightly higher level of complexity, the bonding energy and volume can be treated as adjustable parameters and regressed to minimize deviations in vapor pressure and density. This is the predominate method for most SAFT models. In fact, the critical point method has been systematically avoided for SAFT models other than the ESD model. The regression method requires extensive pure component data. Unfortunately, sufficient data exist for relatively few compounds to regress optimal values or even critical values, and those regressions have already been performed and the results are available. Therefore, the important problem is to characterize the constants when data are few or nonexistent.

Emami et al. have formulated a convenient method that requires little or no experimental data.³⁰ Their method has been developed for the ESD, HR-SAFT, and PC-SAFT models. The method refers to standard literature correlations for ΔH^vap and ρ^liq_298.15 and provides UNIFAC group contribution correlations for the shape factors. This method is facilitated by spreadsheets that are available in Chapter 15 supplements on the textbook’s web site.

Implementations of ESD, HR-SAFT, and PC-SAFT are available from the various authors. A convenient set of implementations that also provides the capability to generate global phase diagrams is available from Cismondi et al.³¹