Equilibrium Criteria

Mole Balance

One may wonder how quantification of the phenomena can be approached in a generalized fashion, but the criteria are presented clearly by Prigogine and Defay (1954) whose proof we reproduce here with modified notation. The first balances that must be satisfied are the material balances. For a binary solution created from n_A moles of A, and n_B moles of B, where n_i is the moles of each specie formed by Eqn. 19.3,

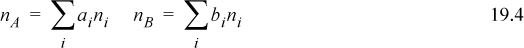
where the summations are over all i true species found in the solution. For example, in the binary solution of Fig. 19.4, Eqn. 19.4 becomes

n_A = 1n_AM + 0n_BM + 2n_A2 + 1n_AB2

n_B = 0n_AM + 1n_BM + 0n_A2 + 2n_AB2

Chemical Potential Criteria

The chemical potentials of the true species are designated by μ_AM, μ_BM, μ_AaiBbi and so forth, and the apparent chemical potentials by μ_A and μ_B. Applying the principles of chemical equilibria to binary Eqn. 19.3, we find

If the total differential of G (Eqn. 17.7) is evaluated at constant T and P, allowing the species to come to equilibria,

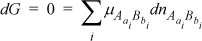
we find by incorporating Eqn. 19.5 and the differential of Eqn. 19.4

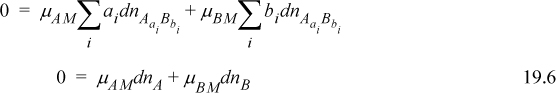
On the other hand, for any binary solution at constant P, T, according to the apparent components

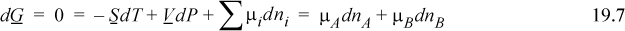
By comparing 19.6 and 19.7 we conclude

Therefore, the apparent (conventional) chemical potential is quantified by a model that calculates the chemical potential of the true monomer species. It should be noted that this proof is independent of the number or stoichiometry of species that are formed in solution.

Fugacity Criteria

The chemical potential criteria may be extended to fugacity. For the apparent chemical potential,

and for the monomer,

Note that for a species that associates, the standard state for the monomer is a mixture state since, even when A is pure, there is a mixture of true associated species. Applying Eqn. 19.8,

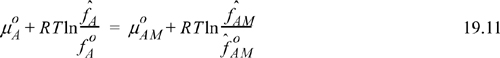
where the standard state is pure component A.

In the event that component A does not associate, the true solution is completely a monomer when A is pure, and

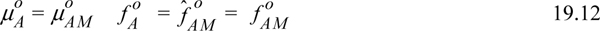
which leads to

The situation when A associates is slightly more complex. Recognizing that the apparent state neglects complexation, the chemical potential of monomer μ_AM in Eqn. 19.10 can be calculated,

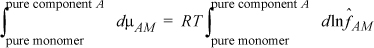
where the lower limit is the hypothetical state of pure monomer, and the upper limit is the monomer state that actually exists in a pure associating solution of A. Integrating both sides, and recognizing the lower limit of each integral as the apparent standard state

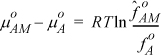
Combining with Eqn. 19.11 again results in Eqn. 19.13. Note that a parallel proof would show

Activity Criteria

Returning to Eqn. 19.9, it can be rewritten in terms of the apparent activity and activity coefficient.

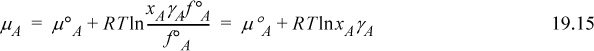
Defining an activity coefficient, α_AM, of the true monomer species, the chemical potential is

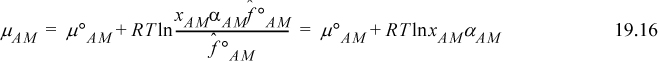
Using Eqn. 19.8 to equate Eqns. 19.15 and 19.16,

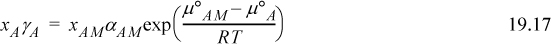
where the exponential term is a constant at a given temperature. The symmetrical convention of apparent activity requires . For a nonassociating species, the exponential term of Eqn. 19.17 is unity by Eqn. 19.12, and thus , . For an associating species  which is the true mole fraction of monomer in pure A, which is not unity. Therefore, the exponential term is simply the reciprocal of the limiting value of the monomer activity . As such, we write

where  for a nonassociating component. A parallel proof would show that

These equations show how the activity coefficient could be less than one even for an “ideal” solution. For example, acetone and chloroform might form an ideal solution in the sense that α_AM=1=α_BM at all concentrations. Complexation would result in x_AM< xº_AM when B was present, such that γ_A < 1. We explore this prospect extensively in Section 19.4.