Entropy Generation via Reactions

When introducing entropy and reversibility in Section 4.11 on page 175, we made a general statement that spontaneous reactions generate entropy. Then, in Section 4.12 on page 177 we derived relations between availability and entropy generation. In that section, we treated a single nonreactive stream. For a reaction in a steady-state open system, Eqn. 4.54 becomes

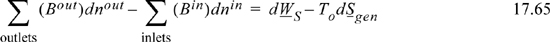
B^out = H^out – T_oS^out and Bⁱⁿ = Hⁱⁿ – T_oSⁱⁿ involve H and S evaluated at the respective T^out and Tⁱⁿ. Enthalpies of mixed streams were first introduced in Chapter 3 and entropies for mixed streams in Chapter 4.⁵ Models for departures functions and excess properties in Chapters 11–15 can be added to improve the mixture property values. The concepts for proper choice of a reference state for properties is important as discussed in Chapter 3 in the section Energy Balances for Reactions on page 113. The flow terms in Eqn. 17.65 are not the same as the Gibbs energy, but the availability will decrease with a spontaneous reaction. Therefore, both sides of the equation will be negative, and shaft work will not be obtained (a normal situation in an industrial reactor), and then entropy is generated. Note that entropy generation can be decreased for a spontaneous reaction only if work is produced. For an electrochemical redox reaction (Chapter 18), the process can produce some electrical work, which is one reason that fuel cells are of much current interest. For a closed-system process, the analysis is similar to the open-system process. The relation is seen most readily if T_o = T (and additional work can be obtained using a heat engine between T and T_o), and at constant pressure, the closed system balance (Eqn. 4.57) becomes

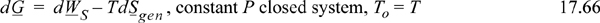
We conclude that production of nonexpansion/contraction work equal to changes in the Gibbs energy is necessary to eliminate entropy generation. Note that it is possible to relate the total work from a reaction to Helmholtz energy using Eqn. 4.58.