Entropy Departure Function

To calculate the entropy departure, adapt Eqn. 8.11,

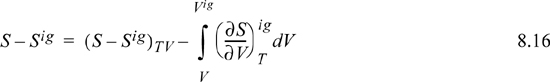
Inserting the integral for the departure at fixed {T, V}, we have (using a Maxwell relation),

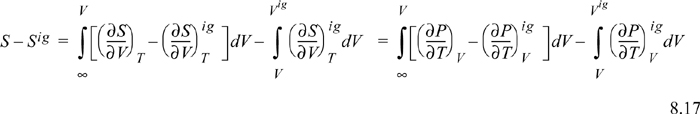
Since , we may readily integrate the ideal gas integral (note that this is not zero whereas the analogous equation for energy was zero):

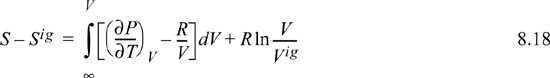
Recognizing V^ig = RT/P, V/V^ig = PV/RT = Z,

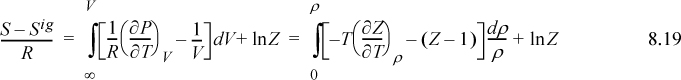
where Eqn. 8.15 has been applied to the relation for the partial derivative of P.

Note the ln(Z) term on the end of this equation. It arises from the change in ideal gas  represented by the integral in Eqn. 8.16. Changes in states like this may seem pedantic and arcane, but they turn out to be subtle details that often make a big difference numerically. In Example 7.4 on page 266, we determined vapor and liquid roots for Z. The vapor root was close to unity, so ln(Z) would make little difference in that case. For the liquid root, however, Z = 0.016, and ln(Z) makes a substantial difference. These arcane details surrounding the subject of state specification are the thermodynamicist’s curse.