Hydrocarbon emission monitoring is an important aspect of environmentally conscious chemical manufacturing and processing. The United States Environmental Protection Agency (EPA) has published guidelines8,9,10 on the calculations of emissions of volatile organic compounds (VOCs), and VOC emissions are monitored in the U.S. Most of the emission models apply the ideal gas law and Raoult’s law and thus the calculation methods are easily applied. While many of the mixtures represented with these techniques are not accurately modeled for phase equilibria by Raoult’s law, the method is suitable as a first approximation for emission calculations. This section explores emission calculations for batch processes. Batch processes are common in specialty chemical manufacture. In most cases, air or an inert gas such as nitrogen is present in the vapor space (also known as the head space). In some cases, the inert head space gas flows through the vessel, and is called a purge or sweep gas. These gases typically have negligible solubilities in the liquid phase and are thus considered noncondensable. There are several common types of unit operations encountered with VOC emissions, which will be covered individually.
Filling or Charging
During filling of a tank with a volatile component, gas is displaced from the head space. The displaced gas is assumed to be saturated with the volatile components as predicted with Raoult’s law and the ideal gas law. Initially in the head space, ![]() and after filling,
and after filling, ![]() , where the subscript head indicates the head space. The volume of liquid charged is equal to the volume change of the head space. The mole fractions of the VOC components are determined by Raoult’s law, and the noncondensable gas makes up the balance of the head space. The moles of VOC emission from the tank are estimated by
, where the subscript head indicates the head space. The volume of liquid charged is equal to the volume change of the head space. The mole fractions of the VOC components are determined by Raoult’s law, and the noncondensable gas makes up the balance of the head space. The moles of VOC emission from the tank are estimated by ![]() for each VOC.
for each VOC.
Purge Gas (Liquid VOC Present)
When a purge (sweep) gas flows through a vessel containing a liquid VOC, the effluent will contain VOC emissions. At the upper limit, the vessel effluent is assumed to be saturated with VOC as predicted by Raoult’s law. For VOC component i,

where ![]() , where the sum is over VOCs only. The variable km is the saturation level, and is set to 1 for the assumption of saturation and adjusted lower if justified when the purge gas is known to be unsaturated. The flow of noncondensables nsweep can be related to a volumetric flow of purge gas using the ideal gas law,
, where the sum is over VOCs only. The variable km is the saturation level, and is set to 1 for the assumption of saturation and adjusted lower if justified when the purge gas is known to be unsaturated. The flow of noncondensables nsweep can be related to a volumetric flow of purge gas using the ideal gas law,

Purge Gas (No Liquid VOC Present)
Vessels need to be purged for changeover of reactants or before performing maintenance. After draining all liquid, VOC vapors remain in the vessel at the saturation level present before draining. The typical assumption upon purging is that the vessel is well mixed. A mole balance on the VOC gives ![]() ; dividing by yi the equation becomes
; dividing by yi the equation becomes ![]() . The left-hand side can subsequently be written ntankdyi/yidt = (PVtank)/(RTtank) · (dyi)/(yidt), and the right-hand side can be written
. The left-hand side can subsequently be written ntankdyi/yidt = (PVtank)/(RTtank) · (dyi)/(yidt), and the right-hand side can be written ![]() . When the sweep gas and tank are at the same temperature, which is usually a valid case, the equation rearranges to
. When the sweep gas and tank are at the same temperature, which is usually a valid case, the equation rearranges to ![]() , which integrates to
, which integrates to

The emissions are calculated by

Heating
During a heating process, emissions arise because the vapors in the head space must expand as the temperature rises. Since vapor pressure increases rapidly with increasing temperature, VOC concentrations in the vapor phase increase also. Detailed calculations of emissions during heating are somewhat tedious, so an approximation is made; the emission of each VOC is based on the arithmetic average of the molar ratio of VOC to noncondensable gas at the beginning and the end of the heating multiplied by the total moles of noncondensable gas leaving the vessel. At the beginning of the heating, representing the VOC with subscript i and the noncondensables with subscript nc, the ratio of interest is (ni/nnc)i = (yi/ync)i = (yiP/yncP)i, and at the end (ni/nnc)f = (yi/ync)f = (yiP/yncP)f. The emission of VOC component i is calculated as

where ![]() , and the sum is over VOCs only. The value of Δnnc is given by
, and the sum is over VOCs only. The value of Δnnc is given by
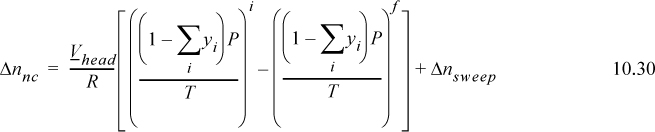
where the summations are over VOCs only and Δnsweep is the total moles of noncondensable that are swept (purged) through the vessel during heating and is set to zero when purging is not used. Eqns. 10.29 and 10.30 can overestimate the emissions substantially if the tank approaches the bubble point of the liquid because ync approaches zero, and then calculations are more accurately handled by a more tedious integration. The integration can be approximated by using the method presented here over small temperature steps and summing the results.
Depressurization
Three assumptions are made to model depressurizations: The pressure is decreased linearly over time; air leakage into the vessel is negligible; and the process is isothermal. The relationship is then the same as Eqn. 10.29, where Δnnc is calculated by Eqn. 10.30 using Δnsweep = 0.
Other Operations
Other operations involve condensers, reactors, vacuum vessels, solids drying, and tank farms. Condensers are commonly used for VOC recovery; however, the VOCs have a finite vapor pressure even at condenser temperatures and the emissions can be calculated by using Eqns. 10.25 and 10.26 at the condenser temperature. Reactors may convert or produce VOCs and, in a vented reactor, the emissions can be calculated by adapting one of the above techniques, keeping aware that generation of gas causes additional vapor displacement and possible temperature rise due to reaction. Vacuum units and solids-drying operations are also direct adaptations of the methods above. Tank farm calculations are more detailed and empirical. Tank emission calculations depend on factors such as the climate and the paint color of the tank. Fixed roof tanks must breathe as they warm during the day due to sunlight, and then cool during the night hours. There are also working losses due to routine filling of the tanks as covered above. Although heating and cooling in a tank with a static level can be treated by the methods presented above, when the levels are also changing due to usage, EPA publications are recommended for these more tedious calculation procedures.
Flash Point
The flash point is a property much different from that represented by the general flash or adiabatic flash discussed earlier. Fire requires fuel, an oxidizer (air in this case), and an ignition source. The flash point is the temperature above which a vapor mixture supports combustion when an ignition source is present. When liquids burn, fire occurs on a liquid surface; the vapors near the surface are burning, not the liquid itself. The flash point is important because it is the temperature at which the Lower Flammability Limit (LFL) concentration is reached at the liquid surface. A flash can also occur entirely in the vapor phase. When burning buildings explode in action movies, the movies are depicting the real condition of the vapors in the building reaching the flash point as plastics and other materials decompose. Fire fighters are very cautious entering buildings where a potential for such explosions exist.
![]() The Chemical Safety Board is a federal agency charged with investigating chemical accidents. The goal is to learn from accidents and improve safety.
The Chemical Safety Board is a federal agency charged with investigating chemical accidents. The goal is to learn from accidents and improve safety.
The Chemical Safety Board (www.csb.gov) tracks accidents in the U.S. chemical industry. The CSB reports that workers continue to be careless with ignition sources near organic solvents. Earlier sections discussed the warming of a tank during the day. As a vented tank warms, emissions may reach the LFL as the day warms. Maintenance on metal tanks often involves grinding or welding, which introduces ignition sources and has resulted in numerous deaths and disfigurements as well as property damage. Raoult’s law may be used to estimate the vapor phase concentrations, and the flash point temperature is approximately the temperature where y·(100%) = LFL. Technically, the LFL defined as a volume percent of combustible material, but it is the same as the mole fraction in an ideal gas. For a mixture, the flash point can be calculated approximately by the empirical relation
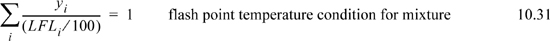
Because combustion requires an oxidizer, each fuel also has an Upper Flammability Limit (UFL) above which there is not enough oxygen present to maintain combustion. Most accidents occur near the LFL, which is the motivation for more discussion of LFL. Both the LFL and the UFL are affected by inerts because of the effect on the ratio of oxidizer to fuel.
Leave a Reply