Effects of Pressure, Inerts, and Feed Ratios

At a given temperature, equilibrium values of the reaction coordinate are affected by pressure, inerts, and feed ratios. The principle that changing the quantities affects equilibrium conversions is known as Le Châtelier’s principle in honor of Henry Louis Le Châtelier who first characterized the phenomenon. An understanding of Le Châtelier’s principle is important for operating industrial reactions. Two important modifications led to significant hydrogen conversions in Example 17.1 even though the equilibrium constant was small—use of pressure and nonstoichiometric feed.

Henry Louis Le Châtelier (1850–1936) was a French chemist. He was elected to the French Académie des Sciences and the Royal Swedish Academy of Sciences in 1907.

Pressure Effects

Pressure has little effect on the activities of condensed species (e.g., the Poynting correction is typically small) and thus it has a primary significance only for reactions with gas phase components. Pressure has important effects when both 1) gas species are involved in reactions and 2) the stoichiometric numbers of gas species are different for reactants and products. When the stoichiometric moles of gas species are the same for reactants and products, P has no effect by the ideal gas approximation, and for nonideal gases only indirect effects due to fugacity coefficients.

The equilibrium constants for ideal gases can be written

This form makes the pressure effect more obvious. As mentioned above, when the stoichiometric number of gas moles is the same for products and reactants, Σv_i = 0 and the pressure effect drops out. When the stoichiometric numbers of vapor reactant moles is greater than the stoichiometric numbers of product vapor moles, an increase in pressure will drive the reaction to higher conversions,. Σv_i < 0. When the stoichiometric gas mole ratios are reversed, a decrease in pressure will help drive the reaction to higher conversions, Σv_i > 0. In Example 17.1 the pressure of 20 bar was important to yield significant conversions. It can be helpful to consider that qualitatively the pressure “squeezes” the reaction towards the side with fewer gas moles. As an exercise, determine the reaction coordinate for the same feed when the pressure is 1 bar.

Inerts

A component that does not participate in a reaction is called inert. Inert gas components often have an indirect, but important effect on the equilibrium reaction coordinate when gas phase species are present. Inerts change the overall mole fractions and thus mitigate the pressure effects. When Σv_i > 0, adding an inert will increase conversion at a fixed total pressure. However, when Σv_i < 0, the mitigation of the pressure effect is undesirable and inerts should be avoided. Qualitatively, the presence of an inert decreases the “squeezing” effect mentioned above.

Nonstoichiometric Feed

Conversions of specific reactants are influenced using nonstoichiometric feed. In Example 17.1, excess CO was fed to the reactor; conversions were 42% (H₂), and 10.5% (CO). Generally, an excess of one reactant will tend to increase conversion of the other reactant. The effect can be seen qualitatively using Eqn. 17.2. For a given K_a, at a certain value of y_CH3OH, a higher value of y_CO results in a lower value of y_H2. When using stoichiometric feed (CO:H2 = 1:2) in Example 17.1, the equilibrium conversions of H₂ and CO are equal (40.6%). Example 17.1 includes both excess CO and a pressure effect. The excess CO in Example 17.1 is high enough to mitigate the beneficial pressure effect in a manner similar to an inert gas. The feed ratio giving highest H₂ conversion for the specified conditions uses less excess CO, (CO:H₂ = 1:1), which results in conversions of 45.2% (H₂) and 22.6% (CO). Use of nonstoichiometric feed is common in industrial reactions because in some cases it helps avoid side reactions in addition to effects on equilibrium.

---

Example 17.3. Butadiene production in the presence of inerts

Consider again the butadiene reaction of Example 17.2 on page 648. Butadiene is prepared by the gas phase catalytic dehydrogenation of 1-butene, at 900 K and 1 bar.

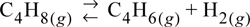
a. In order to suppress side reactions, the butene is diluted with steam before it passes into the reactor. Estimate the conversion of 1-butene for a feed consisting of 10 moles of steam per mole of 1-butene.

b. Find the conversion if the inerts were absent and side reactions are ignored.

c. Find the total pressure that would be required to obtain the same conversion as in (a) if no inerts were present.

In the earlier example, we determined the value at 298.15 K for . Now we need a value at 900 K. The next section explains how the value at 900 K may be obtained. For now, use the following data for  at 900 K and 1 bar:

Solution

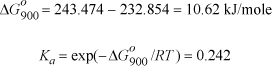
a. Basis of 1 mole 1-butene feed. Set up reaction coordinate, using I to indicate inerts,.

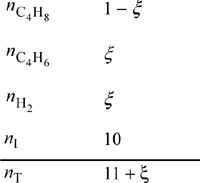
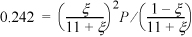
The physical range of the solution is 0 ≤ ξ ≤ 1. P = 1 bar ⇒ 1.242 ξ² + 2.42 ξ – 2.662 = 0 ⇒ ξ = 0.784. For the basis of 1 mol 1-butene feed, the conversion is 78.4%.

b. n_I = 0 and the basis of feed is the same and 0 ≤ ξ ≤ 1. The total number of moles is n_T = 1 + ξ; 1.242ξ² – 0.242 = 0; ξ = 0.44, so conversion decreases to 44% without inert.

c. Rearranging the equilibrium expression for pressure, P^–1 = ξ² / [0.242 · (1 – ξ) · (1 + ξ)], 0 ≤ ξ ≤ 1.

Inserting a reaction coordinate of ξ = 0.784 gives P = 0.152 bar. So the reaction would need to run at a much lower pressure without the inerts to achieve the same conversion. In other words, inerts serve to dilute the fugacities of the products and suppress the reverse reaction since there are more moles of product than reactant.