In Chapter 10 we demonstrated that Raoult’s law requires an ideal solution model for the vapor and liquid phases as well as conditions where the fugacity coefficients can be ignored. In Section 11.1 we have shown that a relatively simple function is able to capture a major correction to Raoult’s law, but we have superficially made the connections to fundamental properties and we must now develop that understanding of how this function is related to component fugacity and Gibbs energy of the mixture.
To perform VLE calculations, we begin with the fundamental criterion ![]() . The fugacity in non-ideal systems is modeled in terms of deviations from either the ideal gas model or the ideal solution model. The Venn diagram in Fig. 11.8 may be helpful in visualizing these relations. Ideal gas behavior is the simplest type of mixture behavior because the particles are non-interacting. This is shown in the center of Fig. 11.8. Clearly, ideal gas behavior is not followed by all mixtures, and therefore ideal gases are a subset of real mixtures. Strictly, ideal gas molecules cannot condense because they have no attractive forces; if fluids were ideal gases, there would be no liquids, and VLE would not occur. However, at low densities, gas molecules are frequently separated far enough that the effective intermolecular potentials are insignificant, and we can frequently model the gas phase as if it is an ideal gas. The fugacity of a component in an ideal-gas mixture is particularly simple; it is equal to yiP, the partial pressure. The ideal gas model is acceptable for most small molecular weight vapors near atmospheric pressure;6 and the primary failure of Raoult’s law is due to the liquid phase where the molecules are closely packed. When the molecules are closely packed in a liquid phase the intermolecular potential is significant for the same molecules whose potential energies could be disregarded in the vapor phase. The size and shape of molecules and differences in chemical functionality at close distances often violate the assumptions of ideal solution behavior. We introduce the concept of the activity and activity coefficient, γi, to correct the ideal mixture model as summarized in Fig. 11.8.
. The fugacity in non-ideal systems is modeled in terms of deviations from either the ideal gas model or the ideal solution model. The Venn diagram in Fig. 11.8 may be helpful in visualizing these relations. Ideal gas behavior is the simplest type of mixture behavior because the particles are non-interacting. This is shown in the center of Fig. 11.8. Clearly, ideal gas behavior is not followed by all mixtures, and therefore ideal gases are a subset of real mixtures. Strictly, ideal gas molecules cannot condense because they have no attractive forces; if fluids were ideal gases, there would be no liquids, and VLE would not occur. However, at low densities, gas molecules are frequently separated far enough that the effective intermolecular potentials are insignificant, and we can frequently model the gas phase as if it is an ideal gas. The fugacity of a component in an ideal-gas mixture is particularly simple; it is equal to yiP, the partial pressure. The ideal gas model is acceptable for most small molecular weight vapors near atmospheric pressure;6 and the primary failure of Raoult’s law is due to the liquid phase where the molecules are closely packed. When the molecules are closely packed in a liquid phase the intermolecular potential is significant for the same molecules whose potential energies could be disregarded in the vapor phase. The size and shape of molecules and differences in chemical functionality at close distances often violate the assumptions of ideal solution behavior. We introduce the concept of the activity and activity coefficient, γi, to correct the ideal mixture model as summarized in Fig. 11.8.
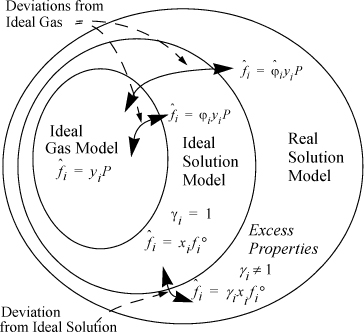
Figure 11.8. Schematic of the relations between different fluid models. Ideal gases are a subset of ideal mixtures, which in turn are a subset of real mixtures. Departure functions (fugacity coefficients) characterize deviations from ideal-gas behavior, and excess properties (activity coefficients) characterize deviations from ideal-solution behavior.
The activity coefficient is defined as a ratio of the component fugacity to the ideal solution fugacity at the same mole fraction:

![]() Activity coefficients are commonly used for highly non-ideal solutions.
Activity coefficients are commonly used for highly non-ideal solutions.
A value of γi = 1 will denote an ideal solution; ![]() is the value of the fugacity at standard state. A standard state is slightly different from a reference state. The standard state is a specified temperature, pressure, and composition. The most common standard state in solution thermodynamics is the pure component at the same temperature pressure as the system. You can see that this is clearly different from a reference state that would stay fixed throughout a series of calculations. For this standard state, standard state fugacity is simply the pure component fugacity which we introduced in Chapter 9, fi. In Fig. 11.8 we also introduce the fugacity coefficient
is the value of the fugacity at standard state. A standard state is slightly different from a reference state. The standard state is a specified temperature, pressure, and composition. The most common standard state in solution thermodynamics is the pure component at the same temperature pressure as the system. You can see that this is clearly different from a reference state that would stay fixed throughout a series of calculations. For this standard state, standard state fugacity is simply the pure component fugacity which we introduced in Chapter 9, fi. In Fig. 11.8 we also introduce the fugacity coefficient ![]() for a component in a mixture to characterize the component fugacity relative to the ideal gas partial pressure. We defer most discussion of the component fugacity coefficients to Chapters 15 and 19.
for a component in a mixture to characterize the component fugacity relative to the ideal gas partial pressure. We defer most discussion of the component fugacity coefficients to Chapters 15 and 19.
Now, let us look rigorously at the development of modified Raoult’s law. For the vapor phase, we begin with the rigorous expression from Fig. 11.8 including deviations from the ideal gas model, ![]() . For the liquid phase, we use an activity coefficient, γi, giving7
. For the liquid phase, we use an activity coefficient, γi, giving7

Typically the Poynting method (Section 9.8) is used to calculate the pure-component liquid phase fugacities, ![]() . Combining these expressions,
. Combining these expressions,
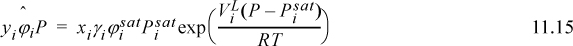
When used in this full form, Eqn. 11.15 is called the gamma-phi method. This may be written in terms of the K-ratio, Ki = yi/xi,
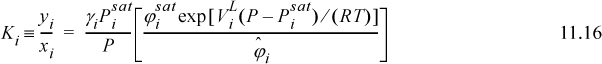
At the low pressures of many chemical engineering processes the Poynting corrections and the ratios of ![]() for the components approach unity. Recalling
for the components approach unity. Recalling ![]() , we find
, we find
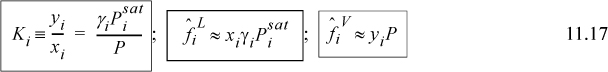
We usually write
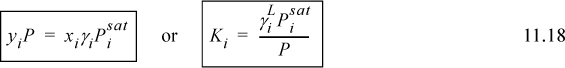
We can see that modified Raoult’s law depends on the fugacity coefficient ratio being close to unity, not necessarily on the ideal gas law being exact. Next, let us demonstrate how the activity coefficient is related to the excess Gibbs energy.
Leave a Reply