Referring back to Fig. 14.1, we may wish to find the combination of x1 and A12 where the system just begins to phase-split. This is known as a liquid-liquid critical point. If it is the highest T where two phases exist (called the UCST, upper critical solution temperature), then we must seek x1 where the concavity is equal to zero at only one composition (if it was less than zero anywhere, then we would just have a regular phase split, not a critical point—refer back to the curve for A12 = 3 in Fig. 14.1). If the concavity is equal to zero at x1 and greater everywhere else, then this must represent a minimum in the concavity as well a point where it equals zero. These two conditions provide two equations for the two unknowns, x1 and T, involved in determining the critical point. Recalling that concavity is given by the second derivative:

A generalization of these concepts to multicomponent mixtures gives
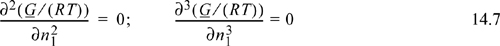
By analogy to the phase diagram for pure fluids, the locus where the second derivative equals zero represents the boundary of instability and is called the liquid-liquid spinodal.
Example 14.6. Liquid-liquid critical point of the Margules one-parameter model
Based on Fig. 14.1 and the discussion of concavity above, it looks like the value of A12 = 2 may be close to the critical point. Use Eqns. 14.6 and 14.7 to determine the exact value of the critical parameter.
Solution
Multiplying through by n and recognizing that we have previously performed the initial part of this derivation (see Eqns. 11.29–11.31) gives
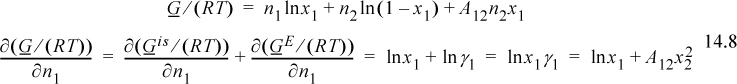
Since this is a binary solution, there is a simple finite relationship between the derivative with respect to mole number and the derivative with respect to mole fraction, leading expeditiously to the expected conclusion:
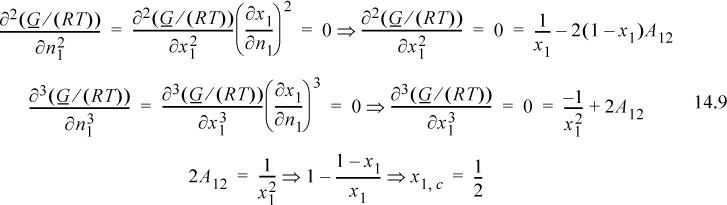

From this example, we can draw a useful conclusion regarding the magnitude of activity coefficients that leads to immiscibility. Based on the Margules model, LLE should occur whenever A12 > 2, and a useful engineering rule of thumb for immiscibility is when the activity coefficients exceed the value of 7.4,
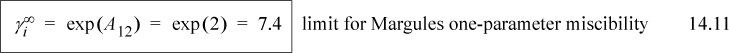
With the capability to determine immiscibility, it is possible to convey some background on one of the most significant scientific challenges currently occupying modern thermodynamicists. This is the problem of phase separation in polymer solutions and polymer blends. The same forces driving these phase separations lead to the extremely important problem of the collapse transition of a single polymer chain in a solvent or mixture. A special kind of collapse describes the protein folding problem. Imagine a bowl of spaghetti formed from a single noodle. After stretching the noodle until it is completely straight, release and watch it collapse into the bowl again. If the noodle was really a protein, it would collapse into exactly the same hooks and crooks as it was before being stretched. The folding is driven by hydrophobic effects, hydrogen bonding, and intramolecular interactions like helix formation. A complete understanding of this phenomenon would greatly facilitate drug design.
Limiting this introductory presentation to liquid-liquid equilibria, the phase partitioning of polymer mixtures is somewhat simpler in that we care only about collections of chains rather than the details of individual chains. Polymer solutions are classified differently from polymer blends in a manner that is superfluous to our mathematical analysis: polymer solutions are blends where the degree of polymerization of one of the components is unity (the small one is known as the solvent). With this minimal background, we can phrase the following problem:
Example 14.7. Liquid-liquid critical point of the Flory-Huggins model
Determine the critical value of the Flory-Huggins χ parameter considering the degrees of polymerization of each component.
Solution
Note that we have already solved this problem for the special case where the two components are identical in size. Then the excess entropy is zero, the volume fractions are equal to the mole fractions, and the Margules one-parameter model is recovered with A12 having nearly the same meaning as the Flory-Huggins χ parameter. To consider the problem of including the degree of polymerization, Nd, we must define the parameter with respect to a standard unit of volume. Nd is the number of monomer repeat units in the polymer. In the presentation below (and most other presentations of the same material), the volume of a monomer of component 1 is assigned as this standard volume (χ′ = Vstd·[δ1– δ2]2/RT; Vstd = V1/Nd,1). Note that we are introducing temperature dependence into χ′. Recalling the formula for the activity coefficient with this notational adaptation, the starting point (Eqn. 11.46) for this derivation becomes:
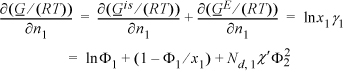
The next step is greatly simplified if we recognize a simple relationship that is very similar to the formula for computing the number average molecular weight from the weight fractions of each component. The analogous formula for the volume can be rearranged in terms of the volume ratio r = V2/V1 as follows:
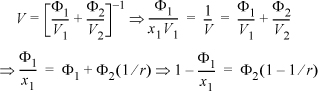
Since this is a binary solution, there is a simple finite relationship between the derivative with respect to mole number and the derivative with respect to volume fraction, leading expeditiously to the general conclusion (note dΦ1 = –dΦ2):
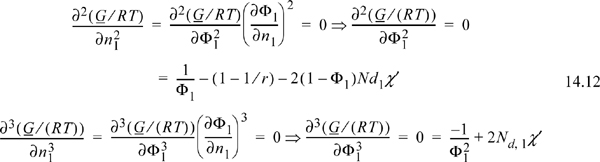
which leads to two important results:
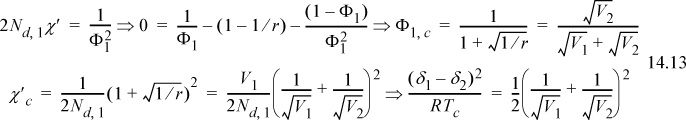
These results suggest that critical concentration decreases to zero with increasing polymer size but the critical temperature approaches a finite limit that is related to the solvent size.
There are a number of significant conclusions that may be drawn from the above example. First, for polymer solutions where (1) is the solvent (i.e., V1<<V2), the critical composition of polymer (2) approaches zero, and the critical temperature is a finite value that depends on the solvent and polymer molar volumes and solubility parameters. Furthermore, the critical temperatures for all polymers in a given solvent should be given by a universal curve with respect to molecular weight when reduced by the solubility parameter difference, although these predictions are only semi-quantitative due to the approximate nature of the Scatchard-Hildebrand theory. For blends where V1~V2, the critical temperature should be proportional to the molecular weight. We have applied several approximations in deriving these formulas, however. Therefore, significant efforts are currently underway to determine whether the formulas presented above are sufficiently accurate to describe the complex phase behavior often observed in polymer solutions and blends. Hanging in the balance is the ability to tailor-make polymer solutions and blends with many commercial advantages, because the ability to manipulate phase behavior successfully often relies on operating within the very sensitive critical region and knowing how to maneuver appropriately.
Leave a Reply