Criteria for Phase Equilibrium

As an introduction to the constraint of phase equilibrium, let us consider an example. A piston/cylinder contains both propane liquid and vapor at –12°C. The piston is forced down a specified distance. Heat transfer is provided to maintain isothermal conditions. Both phases still remain. How much does the pressure increase?

This is a trick question. As long as two phases are present for a single component and the temperature remains constant, then the system pressure remains fixed at the vapor pressure, so the answer is zero increase. The molar volumes of vapor and liquid phases also stay constant since they are state properties. However, as the total volume changes, the quantity of liquid increases, and the quantity of vapor decreases. We are working with a closed system where n = n^L + n^V. For the whole system: V = n^L V^satL + n^VV^satV = n·V^satL + q·n·(V^satV – V^satL) and since V^satL and V^satV are fixed and V^satL < V^satV, a decrease in V causes a decrease in q¹.

Since the temperature and pressure from beginning to end are constant as long as two phases exist, applying Eqn. 9.1 shows that the change in Gibbs energy of each phase of the system from beginning to end must be zero, dG^L = dG^V = 0.

For the whole system:

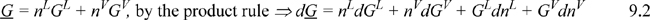
But by the mass balance, dn^L = –dn^V which reduces Eqn. 9.2 to 0 = G^L – G^V or

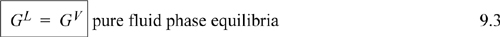
 Gibbs energy is the key property for characterizing phase equilibria.

This is a very significant result. In other words, G^L = G^V is a constraint for phase equilibrium. None of our other thermodynamic properties, U, H, S, and A is equivalent in both phases. If we specify phase equilibrium must exist and one additional constraint (e.g., T), then all of our other state properties of each phase are fixed and can be determined by the equation of state and heat capacities.

Only needing to specify one variable at saturation to compute all state properties should not come as a surprise, based on our experience with the steam tables. The constraint of G^L = G^V is simply a mathematical way of saying “saturated.” As an exercise, select from the steam tables an arbitrary saturation condition and calculate G = H – TS for each phase. The advantage of the mathematical expression is that it yields a specific equality applicable to many chemicals. The powerful insight of G^L = G^V leads us to the answers of many more difficult and significant questions concerning phase equilibrium.