To discuss the concentration of an electrolyte, some terminology conventions are important for clarity. For example, when 0.01 mole of sodium chloride is added to water and diluted to 1 liter at 25°C, the solution results in 0.02 mol/L of ions because it acts as a strong electrolyte. However, we need a method to communicate the solubility of an electrolyte as an entity or on a superficial basis or apparent basis or nominal basis. These terms are used interchangeably in the literature; they refer to the totality of electrolytes in solution as if they were molecular, without dissociation. Formal concentrations (mol/L) are used in chemistry to refer to the molar concentration based on the chemical formula of the substance. The terms “undissociated” and “un-ionized” are different from “apparent.” For species that partially dissociate, the sum of the undissociated and dissociated species comprises the apparent composition. For example, acetic acid does not completely dissociate in aqueous solution, and to communicate most clearly, the terms “nominal,” “superficial,” “as an entity,” and “apparent” are used to refer to the total amount in solution.5 VLE of a weak electrolyte like acetic acid occurs between the undissociated species in the vapor and the undissociated species in the liquid (as we will show later), but a “apparent” perspective would simply consider that there is acetic acid in the vapor and liquid and the apparent activity coefficient of acetic acid is different from what it would be without dissociation. The true distribution of species should be determined by reaction equilibria and Le Châtelier’s principle to characterize the NH4OH that forms and the NH4+ and OH– speciation. Although the apparent perspective may seem oversimplified, the apparent concentration is very important in engineering calculations because it is often the most accessible measure of concentration when multiple species are present. In this text, we strive to consistently refer to “apparent concentrations,” but we may use the equivalent term “superficial concentrations.”
![]() The apparent basis refers to the hypothetical situation as a molecular species.
The apparent basis refers to the hypothetical situation as a molecular species.
The NaCl solution of the preceding paragraph would be described as a 0.01 M apparent concentration of NaCl. On the other hand, the 0.01 M apparent solution of NaCl would have true concentrations of 0.01 M Na+ and 0.01 M Cl–. The convention of terminology is to describe modeled concentrations as “true” concentrations even though the modeled true concentrations often vary for different models for weak electrolytes. [Apparently, some “true” concentrations are more true than others ;-).] In a good model, true concentrations from experiments are represented accurately. Note how the apparent concentration is the only quantity on which everybody can agree.
Concentration Scales For Electrolytes
Throughout introductory chemistry texts, the convention is to express the concentrations in Eqn. 18.5 using molarity. For introductory courses, frequently all the calculations are at room temperature (25 °C), and thus temperature effects are disregarded. For biological systems, the electrolytes are almost always very near room temperature and the density of the solutions is almost always constant, so the convention is to use molarity. However, this choice of concentration as a composition scale has a disadvantage when the temperature changes in industrial processes because temperature affects density, which affects molar concentrations. Thus, an increase in temperature decreases molar concentrations of all species, even when the solution composition does not change. Therefore, for fundamental calculations as a function of temperature, alternative concentration scales are required.
In the case of electrolytes for industrial reactions, it is often easiest to perform calculations based on the number of solute (i.e., electrolyte) molecules relative to the number of solvent (e.g., water) molecules. This can be done with mole fraction or molality. Molality has a disadvantage that the quantity diverges to infinity at high concentration. Nevertheless, it is the dominant convention in the older electrolyte literature for nonideal solution behavior and dissociation constants. Molality approaches molarity at low concentrations near room temperature and thus is a natural extension from the use of molarity. Also, molality has a convenient magnitude at common concentrations. Molality is the moles of species existing in 1 kg of solvent (e.g., water) molecules. If water is the solvent, the number of moles per kg of solvent is 55.509. We use the notation “m” for molality and “M” for molarity. For example, a one molal aqueous solution of sodium chloride is prepared by adding 1 mole of NaCl (58.44 g) to 1 kg of water. The molarity of that solution is slightly less than 1 M since the total volume after addition is greater than 1 liter. Molality and molarity are subtly but distinctly different. The ratio of solute to solvent molecules in all 1 molal solutions will be the same for all solutes in a given solvent. To clarify, a comparison of molality, molarity, and mole fractions for NaCl solutions is provided in Table 18.1. The molality and molarity approach each other at low aqueous concentration near room temperature. For dilute solutions, the molarity and molality can be interchanged as a good approximation. The mole fraction scale, typically with a Henry’s law standard state, is preferred when working with concentrated solutions.6 Molality has a disadvantage that it goes to infinity when the water concentration goes to zero. Formulas for interconversions between concentration scales are summarized in Section 18.24
Table 18.1. Apparent Mole Fraction, Molality, Density and Molarity for Aqueous Sodium Chloride Solutionsa
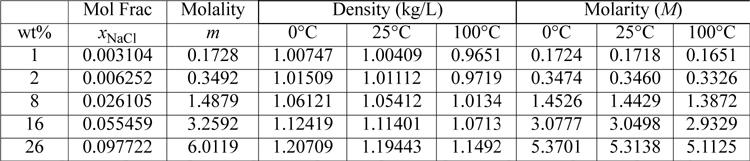
a. Densities are from Washburn, E.W., ed., 1926–1930. International Critical Tables, National Research Council, vol. 3, p. 79.
![]() We use the notation “m” for molality and “M” for molarity.
We use the notation “m” for molality and “M” for molarity.
Standard State for Electrolyte Systems
When molality or molarity is used for concentration, the standard state is selected such that the activity coefficients of the electrolyte species, including the undissociated species, go to unity at infinite dilution. This is similar to the Henry’s law standard state discussed in Section 11.12.7 An unsymmetric convention (cf. Section 11.12) is used in that a Lewis-Randall standard state is applied for the solvent (typically water) and the activity coefficient of the solvent goes to unity when the solvent is pure.
To understand how the conventions are useful, look back at Table 18.1. Note that the mole fraction of water is approximately xw = 0.9 when the solution is 3 m in NaCl (remember NaCl dissociates!). So the use of an activity coefficient of unity for water is reasonable for approximate calculations. The use of an activity coefficient of unity for the electrolytes is exact only at infinite dilution, but can be used as a rough approximation for introductory calculations. We take that approach initially, using ideal solution calculations and the infinite dilution standard state for electrolytes and the Lewis-Randall standard state for the solvent, and later introduce the more rigorous calculation using activity coefficients.
A caution is that various conventions of molarity, molality, and mole fractions exist in the literature.8 Therefore, when using equilibrium constants, the reader must be careful to understand the conventions used to tabulate the values, and must carefully convert the constants if a different scale/convention is to be used for calculations. The convention can sometimes be inferred if the constant is given with units. Interconversion of constants is discussed in Section 18.25.
Solubility and degree of dissociation depend on the solvent. The majority of published equilibrium constants are for aqueous systems. However, many solvents, including amines, pyridines, ammonia, alcohols, esters, and carboxylic acids, are also capable of solvating ions to varying extents. Because the environment of the ion is critical in determination of the extent of solvation, care should be used when modeling dissociation in nonaqueous solvents.
Leave a Reply