Boiling points, freezing points and osmotic pressure are sometimes termed colligative properties. The adjective “colligative” describes phenomena that are dependent on molar concentration and ignore the solution nonidealities. This of course is an approximation. We understand from previous chapters discussing nonelectrolytes that solution nonidealities can be important. However, in the case of dissolved solids such as sodium chloride, which have negligible vapor pressure under common conditions, the partial pressure of water/solvent determines the boiling point because the salt does not contribute measurably to the vapor composition. Likewise, the osmotic pressure and freezing points are dominated by concentration effects. We know that sodium chloride is commonly used to melt snow and ice on sidewalks and roads in cold climates. The salt works because the freezing temperature of the solution is lower than that of pure water. It is more effective on a molar basis than a compound that does not dissociate because it decreases the mole fraction of water to a greater extent, thus decreasing the chemical potential of water. François-Marie Raoult wrote about electrolytes and their melting point depression compared to molecular solutes: “These facts show that, contrary to what I thought until now, the general law of freezing does not apply to the salts dissolved in water. They tend to show that it applies to radicals (ions) constituting the salts, almost as if these radicals (ions) were simply mixtures in dissolutions.”3 To be fair, however, the degree of melting depression is not always the most critical factor when selecting a system for melting depression or boiling point elevation. Automobile radiators commonly use ethylene glycol as an antifreeze. On a molar basis, the ethylene glycol is less effective than a dissociating salt in lowering the freezing point and increasing the boiling point. Nevertheless, the liquid additive is used instead of salt for practical reasons like avoiding solid precipitation or corrosion (especially for NaCl).
Raoult’s study of electrolyte dissociation led to further developments by Jacobius van’t Hoff and Wilhelm Ostwald.
Example 18.1. Freezing point depression
Compare NaCl (used on icy roads), ethylene glycol (used in car radiators), and glucose (used by hibernating frogs) as alternatives for freezing point depression. Consider 5 g of each for 0.1 L (5.55 mol) of water and then compare 0.1 mol of each in 0.1 L of water. For the molar basis, compare the masses used and the effectiveness. Assume NaCl totally dissociates, and use an ideal solution approximation.
Solution
The melting point is calculated with Eqn. 14.24. To calculate mole fractions, the molecular weights are NaCl 58.44, ethylene glycol (EG) 62.07, and glucose 180.16. For 5 g of each, the molar amounts are 0.0855 mol, 0.0805 mol, and 0.027 mol, respectively. The mole fractions of water in the solutions (recall that NaCl forms two moles of ions!) are xH2O = 5.55/(5.55 + 2·0.0855) = 0.970, xH2O = 5.55/(5.55 + 0.0805) = 0.986, xH2O = 0.995, respectively, and
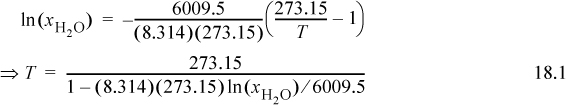
The freezing points for 5 g of each are 270.0 K, 271.7 K, 272.7 K for depressions of 3.2°C, 1.5°C, and 0.5°C respectively. NaCl is more effective than an equivalent mass of EG. Frogs must generate a very concentrated solution of glucose to keep from freezing while hibernating (though concentrated glucose also forms a metastable subcooled liquid easily). For 0.1 mol of each, the mol fractions are xH2O = 0.965, xH2O = 0.982, xH2O = 0.982, with freezing points of 269.6 K, 271.3 K, 271.3 K for depressions of 3.6°C, 1.9°C, and 1.9°C, respectively. There is no difference between the last two solutes because they do not dissociate. The masses needed for 0.1 mol are 5.8 g, 6.2 g, 18.0 g. On a mass basis, NaCl is more effective than glucose even though only one-third as much is used. For EG and glucose, 0.1 mol of each gives the same melting depression, but the mass of glycol is about one-third because the molecular weight is smaller.
Osmotic pressure was discussed in nonelectrolytes in Section 11.13 on page 449. For electrolyte systems a primary difference is that the dissociation of strong electrolytes creates a larger effect on osmotic pressure at the same molar concentration. Look back at Eqn. 11.71. The osmotic pressure is related to the logarithm of the activity of water. When a monovalent electrolyte dissociates, it doubles the effect on the activity relative to an undissociated molecular species (with the ideal solution approximation). Sodium chloride (MW = 58.4 g/mol) and propanol (MW = 60.1 g/mol) have similar molecular weights, but when dissolved in water, to achieve a given osmotic pressure, only about half as much mass of salt is required at low concentrations.
Example 18.2. Example of osmotic pressure
Consider the solutes from Example 18.1 assuming complete dissociation of NaCl and ideal solutions. (a) Compare the osmotic pressure for 0.1 mol of each in 0.1 L of water at 298.15 K. (b) What concentration of NaCl (wt%) is isotonic with human blood?
Solution
a. The mole fractions have been calculated in Example 18.1 as 0.965, 0.982, and 0.982. The osmotic pressure is given by Eqn. 11.71. The osmotic pressure for an ideal solution is
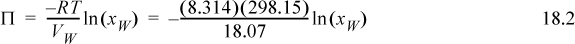
Inserting the mole fractions of each, the osmotic pressures are 4.89 MPa, 2.5 MPa, 2.5 MPa. In a reverse osmosis system, a solution of NaCl requires much more pressure to purify than a solution of a nonelectrolyte with the same apparent concentration.
b. Isotonicity with human blood is defined in Section 11.13 on page 449 as having a concentration that is 0.308 mol/L of solute. Since two ions are obtained for each NaCl that dissociates, this corresponds to 0.154 mol/L of NaCl, or 8.99 g/L. Assuming the concentration is sufficiently low, a dilute aqueous solution corresponds to a density of 1000 g/L. Therefore, the weight fraction is 9/1000 = 0.009 or 0.9wt%. This is commonly known as “physiological saline” or just “saline.”
Vapor-liquid equilibria is also affected by electrolytes. In many cases the electrolyte can be considered to be nonvolatile, such as with sodium chloride. Below we consider the equilibrium condition where salt is only in the liquid phase. In actual application, some salt may be entrained in aerosol droplets as is well known in ocean-side communities where corrosion from salty aerosols is common, but this is not an equilibrium phenomenon. On the other hand, many electrolytes are volatile, such as HCl and acetic acid, so the following analysis will not apply in exactly the same manner.
Example 18.3. Example of boiling point elevation
Consider the solutes from Example 18.1. Compare the bubble points for 0.1 mol of each in 0.1 L of water at 1.013 bar. Consider complete dissociation of NaCl and ideal solutions. Ignore volatility of EG.
Solution
This will be a bubble-temperature calculation. Because the solutes are nonvolatile (ignoring volatility of EG), yH2O = 1. The bubble-pressure condition is
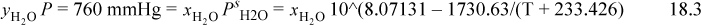
Using the Antoine equation for water and the mole fractions from Example 18.1, the bubble temperatures are found by using an iterative solver to be 101°C, 100.5°C, and 100.5°C, respectively. Again, the salt has a larger effect due to its dissociation.
Typically, the analysis of electrolyte dissociation is treated in the reaction equilibrium framework termed speciation, modeling the dissociation into ionic species as a chemical reaction. When multiple phases exist, simultaneous reaction and phase equilibria must be solved. The general term electrolyte refers to a species that dissociates into ions in solution.
Leave a Reply