Chemical-Physical Theory

The assumptions of ideal chemical theory are known to be oversimplifications for many systems and physical interactions must be included. For a liquid phase, the activity coefficients of the true species can be reintroduced. Then

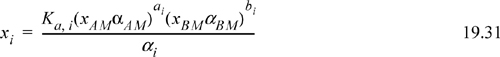
Utilizing this result with Eqns. 19.20 and 19.22, the following equations are obtained:

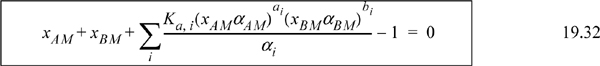
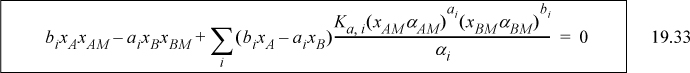
Since most activity coefficient models require two parameters per pair of molecules, the number of parameters becomes large. In addition, any parameters for the complex must be estimated or fit to experiment since the complex cannot be isolated. Solution of the equations is more challenging because the true activity coefficients must be updated with each iteration on x_AM and x_BM.

For chemical-physical theory applied to the vapor phase,

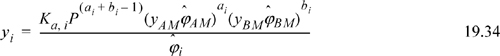
Eqns. 19.20 and 19.22 then become

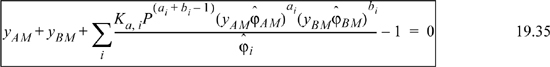
The physical properties of the complex must also be modeled with this approach, and the same challenges for solving the equations are present as discussed above for chemical-physical theory of liquid phases.

An interesting study has been performed by Harris⁸ for acetylene in n-hexane, butyrolactone, and n-methyl pyrrolidone at 25°C. In this study, a simplified van Laar model was used to model the physical deviations, which resulted in one physical parameter. Naturally, the acetylene + n-hexane does not exhibit solvation, but the other binaries do, with the pyrrolidone showing the strongest complexation. Further, the n-hexane system has positive deviations from Raoult’s law across the composition range, the pyrrolidone shows negative deviations, and the lactone shows both positive and negative deviations. All three systems are accurately modeled using two parameters each—one chemical parameter and one physical parameter.

Another approach to the chemical-physical theory is to use the Flory-Huggins theory for the physical contributions. This is the approach of Coleman and Painter in modeling polymer solutions. The Coleman-Painter model leads to complications in the extension to ternary mixtures, however, owing to several details in their perspective on chemical networks.⁹

Multicomponent chemical-physical theory can be achieved most elegantly with Wertheim’s theory which we will discuss in the next section.¹⁰ Wertheim’s theory characterizes chemical interactions from the perspective of the acceptor or donor sites instead of the species. This simplifies to the counting of nonbonded sites, especially for multicomponent systems, and the nonbonded sites can be related to the monomer fraction, which suffices to define the solution thermodynamics. Wertheim’s theory requires a complementary physical theory for the nonchemical attractive and repulsive interactions. Briefly, chemical interaction is short-ranged, so variations in bonding are affected by the frequency of species coming into contact. Repulsive interactions dominate the frequency of contact (specifically, g(σ)). We can estimate g(σ) for spherical molecules with the Carnahan-Starling equation. For nonspherical molecules, we can imagine that they are composed of spherical segments. Then the role of the attractive contribution is like that of a spherical molecule, to provide a disperse field of attractive energy that acts between spherical entities and reduces the pressure. This leads to a remarkably compact and self-consistent model of chemical-physical equilibria.

Before we begin our discussions of Wertheim’s theory, let us mention an additional approach to chemical-physical theory is provided by Heidemann and Prausnitz.¹¹ They showed that reasonable assumptions about the van der Waals parameters of monomers, dimers, trimers, and so on leads to a closed form solution for the compressibility factor and fugacity coefficient. Similar to Wertheim’s theory for pure fluids, the Heidemann-Prausnitz method provides a complete chemical-physical theory, describing all variations with density, temperature, composition, and chemistry. However, similar to the Coleman-Painter theory, this method has complications in the extension to multicomponent mixtures. Suresh and Elliott¹² showed that the Heidemann-Prausnitz method is equivalent to Wertheim’s theory subject to certain assumptions about the change in heat capacity due to reaction. In the interest of covering the most general method, we focus now on Wertheim’s theory, but we introduce concepts using the Heidemann-Prausnitz perspective as a simple way of illustrating several of the more striking results derived from Wertheim’s theory. This is necessary because the rigorous proofs of Wertheim’s theory of Wertheim’s original publications go beyond the introductory scope envisioned here.