We have seen that the Gibbs energy is the key property that must be used to characterize phase equilibria. In the previous section, we have used Gibbs energy in the derivation of useful relations for vapor pressure. For our discussions here, we have been able to relate the two phases of a pure fluid to one another, and the actual calculation of values of the Gibbs energy were not needed. However, extension to general phase equilibria in the next chapters will require a capability to calculate departures of Gibbs energies of individual phases, sometimes using different techniques of calculation for each phase.
Values for Gibbs energy departures are needed for further generalization of phase equilibria.
By observing the mathematical behavior of Gibbs energy for fluids derived from the above equations, some sense may be developed for how pressure affects Gibbs energy, and the property becomes somewhat more tangible. Beginning from our fundamental relation, dG = –SdT + VdP, the effect of pressure is most easily seen at constant temperature.
Starting point for many derivations.
Eqn. 9.13 is the basic equation used as a starting point for derivations used in phase equilibrium. In actual applications the appearance of the equation may differ, but it is useful to recall that most derivations originate with the variation of Eqn. 9.13. To evaluate the change in Gibbs energy, we simply need the P–V–T properties of the fluid. These P-V-T properties may be in the form of tabulated data from measurements, or predictions from a generalized correlation or an equation of state. For a change in pressure, Eqn. 9.13 may be integrated:
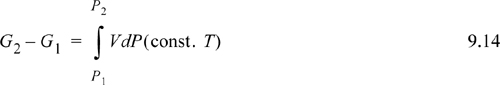
Methods for calculating Gibbs energies and related properties differ for gases, liquids, and solids. Each type of phase will be covered in a separate section to make the distinctions of the calculation methods clearer. Before proceeding to those analyses, however, we consider a problem which arises in the treatment of Gibbs energy at low pressure. This problem motivates the introduction of the term “fugacity” which takes the place of the Gibbs energy in the presentation in the following sections.
Gibbs Energy in the Low-Pressure Limit
The calculation of ΔG is illustrated in Fig. 9.2, where the shaded area represents the integral. The slope of a G versus P plot at constant temperature is equal to the molar volume. For a real fluid, the ideal-gas approximation is valid only at low pressures. The volume is given by V = ZRT/P; thus,
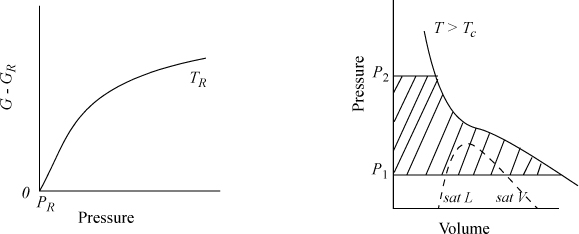
Figure 9.2. Schematic of dependence of G on pressure for a real fluid at TR, and an isothermal change on a P-V diagram for a change from P1 to P2.
which permits use of generalized correlations or volume-explicit equations of state to represent Z at T and P.4 Of course, we may also use Eqn. 9.13 directly, using an equation of state to calculate V. Both techniques are shown later, but first the qualitative aspects of the calculations are illustrated.
For an ideal gas, we may substitute Z = 1 into Eqn. 9.15 to obtain
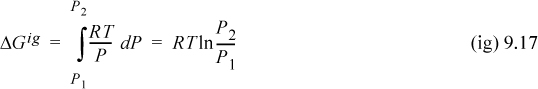
Both dG and dGig become infinite as pressure approaches zero. This means that both Eqns. 9.15 and 9.16 are difficult to use directly at low pressure. However, as a real fluid state approaches zero pressure, Z will approach the ideal gas limit and dG approaches dGig. Thus, the difference dG – dGig will remain finite, and goes to zero as P goes to zero. Thus,
dG – dGig = d(G – Gig)
which is simply the change in departure function. Therefore, we combine Eqns. 9.15 and 9.16 and write:
Differential form of the Gibbs departure.
This relates the departure function to the P-V-T properties in a way that we have seen before. If you look back to Eqn. 8.26, that equation looks different because we are integrating over volume rather than pressure, but they are really related. We use this departure to define a new state property, fugacity, to describe phase behavior. We reserve further discussion of pressure effects in gases for the following sections, where fugacity and Gibbs energy can be considered simultaneously. The generalized treatment by departure functions is also discussed there.
Leave a Reply