Biological Reactions

Oxidation States and Degree of Reduction

Oxidation states, introduced in Section 18.11, provide an important balance condition for any chemical process, but particularly for biochemical reactions and fermentations. Recall that glucose oxidation to CO₂ and H₂O is an important energy-generating reaction in eurakyrotic cells to permit synthesis reactions. The oxidation of glucose or other foodstuffs provides electrons for reducing other species. For biological reaction networks, an electron balance can provide critical analysis of feasible products. CO₂, H₂O, N₂, and O₂ in any mixture cannot sustain biological life in the absence of other energy inputs. Therefore, such a mixture constitutes a useful reference point for a scale known as the degree of reduction.¹⁹ The degree of reduction provides a means to compare the overall electrons in a substance and the energy that can be gained by metabolically converting them to a mixture of CO₂ and H₂O. Combustion of a carbon-containing substance with the generic formula C_fH_aO_b follows the balance,

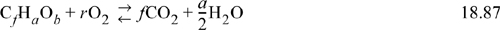
It is easy to show using stoichiometry that r = f + a/4 – b/2. The oxidation state of oxygen in O₂ is 0, and in products is –2. Thus, four electrons are transferred to oxygen atoms for each mole of O₂. The moles of electrons transferred to oxygen from the carbon compound are thus 4r = 4f + a – 2b, where the degree of reduction multipliers are +4 for C, +1 for H, and –2 for O. Nitrogen, sulphur, and phosphorous are often supplied to fermentations, and the reduction multipliers are selected such that reduction numbers are zero in the supply.²⁰ When the N supply is ammonia, the multiplier for N is given a value of –3. For H₂SO₄ as the source, the multiplier for S is +6, and for phosphoric acid as a source, the multiplier for P is +5. To apply an electron balance, the reduction multipliers are used, not the oxidation states. Consider reaction of acetaldehyde. For acetaldyhde (C₂H₄O) the reduction calculation is 2(+4) + 4(+1) + 1(–2) = 10; for O₂ the calculation is r·2·(–2) = (5/2)·2·(–2) = –10; for a net of 0 on the left-side. For CO₂, 1(+4) + 2(–2) = 0, for H₂O, 2(+2) + 1(–2) = 0, and the right-side is also 0. Though each side is not always zero, the two sides will balance.

For carbon-containing compounds the degree of reduction, γ_red, is often expressed per mole of carbon, (known as a basis of C-moles). For C_fH_aO_bN_cS_dP_e,

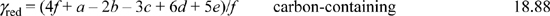
Thus for acetaldehyde above, γ_red = 10/2 = 5 per C-mole. Glucose (C₆H₁₂O₆), has a degree of reduction of (4(6) + 12 – 2(6))/6 = 4 per C-mole. Hexane (C₆H₁₄) is a more highly reduced species, with a degree of reduction of (4(6) + 14)/6 = 6.33. For molecules containing multiple atoms of carbon, the degree of reduction can expressed in terms of moles or C-moles. For example, 180 g of glucose (M_w = 180), can be described as 1 mole of C₆H₁₂O₆, or as six C-moles of CH₂O, (M_w = 30). An average elemental formula for cell mass is CH_1.8O_0.5N_0.2, with a degree of reduction of 4.2 per C-mole, slightly higher than glucose. For compounds not containing carbon, the degree of reduction is expressed per mole of that compound. For the compound H_aO_bN_cS_dP_e,

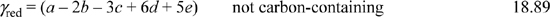
A fermentation can be represented with a pseudo-reaction, balancing inputs and outputs. For example, on the basis of one C-mole of substrate CH_aO_bN_cS_d,

CH_aO_bN_cS_d + Y_o(O₂) + Y_n(NH₃) + Y_aux(CH_e O_fN_gS_h) → Y_biomass(CH_iO_jN_kS_l) + Y_product(CH_m O_nN_pS_q) + Y_CO2(CO₂) + Y_w(H₂O) + Y_S(H₂SO₄)

where the Y values on the left are for the nutrients and on the right are for the products and by-products. The number of moles for each species is the value of the corresponding coefficient Y.

The number of electrons must balance for reactants and products using the degree of reduction relative scale. An electron balance is a useful method for performing mass balances on fermentation processes. The number of electrons in a feed or product is simply ∑(C-moles or Y)_iγ_i. Thus, you can see that if you envision a biological process converting a mole of glucose to a mole of hexane, the fermentation needs an additional source of electrons to perform the reduction and the required C-mols of the substance supplying the electrons can be calculated. Some fermentations “fix” CO₂, such as the succinic acid (C₄H₆O₄) fermentation. CO₂ and water have a degree of reduction of 0, and succinic acid has a degree of reduction of 3.5, so 3.5 electrons must be furnished from some other source for each C-mole of succinic acid produced (14 electrons per mole of succinic acid). Roels¹⁹ has presented a simple approximate correlation between the degree of reduction and availability and degree of reduction and heat of combustion. Applying the availability concepts from Section 4.12 (with different notation), Roels analyzes heat production and irreversibilities in aerobic and anaerobic fermentations. Grethlein, et al. used electron balances to determine CO and CO₂ utilization in syngas (mixtures of H₂, CO, CO₂) fermentations to produce methanol.²¹ Shuler and Kargi show that the combination of the electron balance and elemental balances together can be used to determine the fraction of product, biomass by-product, and fraction lost to CO₂.²²

Binding Polynomials

To treat driving forces for reactions such as electron transfers and chemical equilibria, transformed Gibbs energies of formation are used along with their related apparent equilibrium constants. To perform the transformation, we use a binding polynomial when a species can exist in several bound states. Here we discuss binding polynomials that are helpful for relating the apparent molar concentration to the concentrations of individual species.

When we discussed H₃PO₄ in Section 18.9, we developed a recurring relation for the dissociation in Eqn. 18.50. In that section, we considered H₃PO₄ to be the “parent” molecule that lost successive hydrogens with each dissociation. However, an alternative perspective is to consider PO₄^3– to be a binding receptor for H⁺ “ligands.” If we consider the addition of H⁺ to be successive binding reactions, the first binding constant is the reciprocal of the last dissociation constant, , and other binding/dissociations can be similarly related. From this perspective, the binding receptor, PO₄^3– is the species of interest. A total balance on the species from this perspective replaces Eqn. 18.50 with the equivalent relation (left as a homework problem),

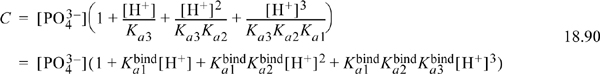
Either of the arguments in parentheses is called a binding polynomial, P_bind. Many successive binding events can be represented by this recursion pattern with either the dissociation constants or the binding constants. The concept illustrated here for three protons as ligands can be generalized to other binding receptors and ligands. Each term in the binding polynomial is proportional to the concentration of a bound species, and the sum represents all possibilities. The fraction of the binding receptor in a given state is (in terms of the binding reaction constant),

where we have generalized to an arbitrary ligand concentration [x], t is the maximum number of ligands, and we have generalized the bonding constant, (K₀ = 1). For our phosphoric acid example,  (recall for our example that the first binding is related to the third dissociation). In the analogy here, the H⁺ serves as the ligand. A key quantity in comparing models of binding to experiments is known as the average number of ligands bound per receptor as a function of ligand concentration. Using binding constants, the average ligands per receptor are calculated by the sum of the number of ligands multiplied by the fraction given by Eqn. 18.91,

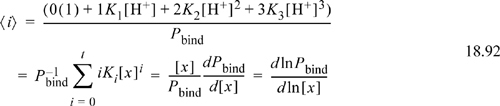
An equivalent expression can be obtained using P_bind in terms of the dissociation constants from Eqn. 18.90.²³ If the binding constants (or dissociation constants, which are the reciprocal of each) are known, then the average binding number can be found as a function of ligand concentration. Note that the average binding number does not depend on the receptor concentration. The binding polynomials are used in transforming the individual Gibbs energies to the apparent Gibbs energy of formation for a family of receptors as we show later.

Energy Carriers in Biological Systems

When introducing biological reactions in Section 3.7, we mentioned the use of carbohydrates, fats, and proteins as food sources. We know that sugars are not “burned” using a single step in the human body. The human body could not survive the adiabatic temperatures of a single-step oxidation. However, biological systems oxidize sugars to CO₂ and water. The reactions that disassemble these foods or other energy storage molecules are termed catabolic reactions. Reactions that build new structures are termed anabolic reactions. Biological systems have a clever way of carrying out the energy transformations. The body carries out the oxidation in small steps, using enzymes to pair endergonic steps with highly exergonic steps. Biological systems transfer and store energy by either 1) forming and breaking bonds; 2) performing redox reactions using electron carriers. A main carrier of energy captured by forming bonds is a molecule called adenosine triphosphate, or ATP as shown in Fig. 18.12. In the process of glycolysis, two ATP molecules are used to transfer two phosphates to glucose (a 6-carbon sugar), modifying it to facilitate subsequent isomerizations and production of two molecules of glyceraldehyde 3-phosphate. Then, the two aldehydes are oxidized to a phosphorylated carboxylic acid in coupled reactions, reducing nicotinamide adenine dinucleotide,²⁴ NAD⁺ to NADH (see Fig. 18.12), storing electrons for other reactions. The two ATP molecules which earlier became ADP are regenerated. In the final step of glycolysis, pyruvate is produced, along with transforming two additional molecules of ADP to ATP, storing additional energy. CO₂ is produced in subsequent reactions when the pyruvate is decarboxylated. Another biological electron carrier is flavin adenine dinucleotide, FAD (oxidized), which is reduced to FADH₂ in other reactions. Similar to the NAD reduction that occurs on the nicotinamide, the riboflavin moiety is reduced, in this case with two hydrogens. The biological networks are quite complex, and this text is not intended to serve as an introduction to biological networks. The goal of the next few subsections is to explain the methods used for calculation of thermodynamic driving forces and equilibrium constants in biochemical reactions.

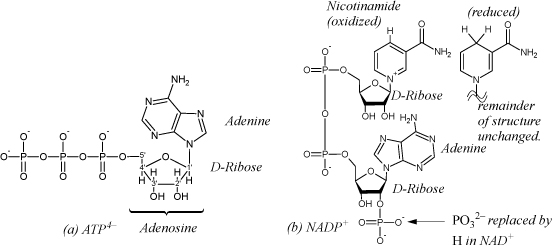
Figure 18.12. (a) Structure of adenosine triphosphate in the form stable at high pH, ATP^4–. Adenosine diphosphate (ADP) has two phosphates; adenosine monophosphate (AMP) has one; adenosine has none. (b)Nicotinamide adenine dinucleotide phosphate, NADP⁺. Nicotinamide also shown reduced, as in NADPH or NADH.

Adenosine triphosphate (ATP), diphosphate (ADP) and monophosphate (AMP) shown in Fig. 18.12 are primary carriers of energy in eukaryotic biological systems, and the distribution of phosphate species is important to represent. ATP can bind up to five protons at low pH (the four on the phosphates plus one on the NH₂). As the pH is lowered, the average number of bindings will undergo a continuous increase until all “receptor” sites are filled at low pH. The individual species are denoted ATP^4–, HATP^3–, H₂ATP^2–, H₃ATP^–, H₄ATP, and H₅ATP⁺. ATP can also bind other cations, one of principle importance being Mg²⁺, and the relevant species are MgATP^2–, MgHATP^–, and Mg₂ATP. Similar to the situation discussed above with phosphoric acid, each ATP dissociation has a known dissociation constant. The notation [ATP] will be used to represent the apparent concentration of ATP in all forms. The distribution of phosphate species is also important as discussed here because phosphates are transferred to/from molecules during many of the biological cycles. The pH and pMg are natural variables for determining the distribution of species using P_bind and Eqn. 18.91.

Biological Standard State and Apparent Equilibrium Constants

Biologists work on the molar concentration scale with standard state properties at 298.15 K, 1 bar and a standard concentration of 1 M, except water is kept on the Lewis-Randall scale, analogous to the molal treatment. The 1 M standard state is awkward in biological systems because the standard state of [H⁺] is a 1 M solution with a pH near 0. Gibbs energy changes based on such a standard state requires a large correction to physiological pH. However, it is convenient to transform the Gibbs energy such that pH and/or pMg may be held constant. Until this point in the text, we have utilized Gibbs energy for analyzing chemical and phase equilibria because it is minimized at constant T and P. If a system were at constant T and V, then the Helmholtz energy would be the correct property minimized, and if at constant S and V, then U would be minimized (note the relation between the natural variables and the minimized property). Biological systems are pH buffered, and when a biological reaction occurs, it occurs at a constant T, P, and pH, and often other ion concentrations are constant, such as Mg. The convention is to transform the Gibbs energy calculations to a pH (and ion concentration) of interest and use a potential that measures the driving forces at constant pH. The process of transformation is special for H⁺ “receptors” such as ATP^4–, PO₄^3–, and other species such as ADP and AMP which lead to a distribution of species. The collection of a given receptor populated with various numbers of ligands are known as a family of pseudoisomers. The transformed properties are denoted with ’. In a similar way, binding of Mg²⁺ is important for ATP, ADP, and AMP. An additional transformation can be made to provide Gibbs energies when pMg = –log[Mg²⁺] is held constant, denoted using the same ’.

 Gibbs energies and redox potentials transformed to a specific pH and pMg are indicated using ’.

The transformed Gibbs energy has some interesting effects on the way that reactions are written and balanced. In this section, we present two main concepts: 1) balancing of reactions in the transformed framework; and 2) relationships between the apparent equilibrium constant and the equilibrium or nonequilibrium concentrations. In this section, we focus on applications where the apparent equilibrium constants are known or determined from apparent equilibrium concentrations. Details on the steps to calculate the apparent equilibrium constants from Gibbs energies of formation are provided in Section 18.17.

When the Gibbs energy is transformed for H, the pH of the solution is considered to be buffered and the surrounding solution is then a sink/reservoir for H⁺ ions. This means that when we write isolated chemical reactions, H is not conserved because the surrounding solution is a sink/reservoir. Therefore, a single reaction in this environment does not cause the pH to go up or down. When we write chemical reactions, we write them without balancing H or H⁺. Because we ignore a cation, H⁺, we also ignore the charge balance for chemical reactions. Analogous arguments apply if the transformation is done for Mg²⁺, and we ignore the balance on Mg.

 For biological reactions using transformed Gibbs energies, the H, Mg balances, and charge balances are ignored.

 Families of pseudoisomers are handled by using the apparent concentrations and apparent Gibbs energies.

 Gibbs energies of formation and equilibrium constant for depend on pH, pMg, ionic strength, and T due to the conventions.

 Transformed Gibbs energies in biology are rigorously related to concentrations.

Another convention of biological thermodynamics uses the apparent concentrations/Gibbs energies for families of pseudoisomers instead of tracking the individual species. This applies to species like phosphate and ATP. Looking at Eqn. 18.90, it is obvious that the distribution of phosphate species is completely determined by the buffered pH. Similar arguments apply to ATP, ADP, or other H⁺ receptors except that Mg²⁺ is simultaneously considered. The approach is to write equilibrium constants that use the apparent concentrations of H⁺ and Mg²⁺ receptors, and absorb the calculations of the distribution and electrolyte nonidealities into Gibbs energies of formation and the equilibrium constants. Details on the mathematics and thermodynamics are explained in Section 18.17, but the details are not important for applications. For applications, the important principle is to recognize that the Gibbs energies of formation and equilibrium constants change significantly with pH, pMg, ionic strength, and temperature. The quantities must be available or calculated at the specific conditions before the equilibrium calculations are performed. However, once they are available, they can be applied with easy hand calculations to determine driving forces or equilibrium conditions. The biological molar standard states and the transformations result in

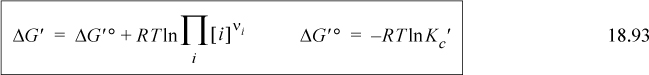
Consider the hydrolysis reaction of ATP to release a phosphate and produce ADP and phosphate,

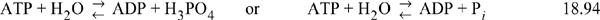
where the left-hand notation writes phosphate as phosphoric acid, and the right-hand notation writes phosphate as a generic P_i. Since ATP, ADP, and phosphoric acid are all distributions of receptor pseudoisomers, the right-side notation is more common in biological publications. The equilibrium constant, at a specified T, pH, and pMg would be written,

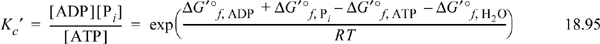
Since the biological standard state uses molar concentrations, the transformed equilibrium constant does also. Note that water is included in the Gibbs energy calculation, but not in the equilibrium constant because the standard state for water is purity and the solution is nearly pure, even though it is transformed.

---

Example 18.10. ATP hydrolysis

a. Calculate the transformed standard state Gibbs energy of reaction and equilibrium constant K_c′ for hydrolysis of ATP at pH_c = 7, pMg = 3, 298.15 K, ionic strength, I = 0.25 m, where the following data apply.

b. Show whether the reaction is endergonic or exergonic at the above conditions when the apparent concentrations are^a [ATP] = 0.00185 M, [ADP] = 0.0014 M, [P_i] = 0.001 M. If the reaction is exergonic, at what concentration of ADP does it reach equilibrium if the concentration of phosphate and ATP are constant?

a. In the human body, [ATP]/[ADP] ~ 10. Alberts, B.; Bray, D.; Hopkin, K.; Johnson, A.; Lewis, J.; Raff J.; Roberts, K.; Walter, P. Essential Cell Biology, 3rd ed., New York: NY, Garland Science, (2010), pg. 465.

Gibbs energies of formation at pH_c = 7, pMg = 3, 298.15K, I = 0.25 mol/kg

Solution

First, note that the Gibbs energy of water is different from the value in Appendix E because of the transformation. The transformed standard state Gibbs energy of reaction is –1426 – 1060 + 2298 + 156 = – 32 kJ/mol. The equilibrium constant will be .

b. The propensity for reaction at the given concentrations is 

The reaction is even more strongly exergonic than the standard state. Equilibrium occurs when [ADP] = k_c^′[ATP]/[P_i] = 5.3×10⁸(0.00185)/0.001 = 9.8×10⁸M. Of course, such a high concentration never happens, so the reaction is always favorable at reasonable concentrations. Instead of hydrolyzing ATP and “losing the energy,” the phosphate is transferred to glucose in a coupled reaction, the subject of a homework problem.

---

---

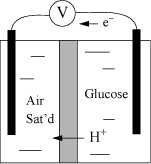
Example 18.11. Biological fuel cell

A biological fuel cell is a portable electrical source that can be refueled. Electrical current is generated by a biological redox couple. In an ideal fuel cell, the enzymes would be immobilized on the electrodes and maintain the same activity as if free. In the conceptualized fuel cell on the right, glucose is to be oxidized to gluconolactone in the right cell, catalyzed by immobilized glucose oxidase. Oxygen is excluded from the right cell to avoid loss of electrons by bulk oxidation. The left cell is saturated with air, and a reduction of O₂ to H₂O₂ catalyzed by immobilized laccase is envisioned. Electrons are to flow through the external circuit and H⁺ is to flow through the membrane. Each side of the cell is buffered to pH_c = 7, I = 0.25 M at T = 298.15 K. Suppose the concentrations on the right side are [glucose] = 0.1 M, [gluconolactone] = 0.05 M, and on the left side [H₂O₂] = 0.05 M. Determine the transformed standard state half-cell potentials and the voltage expected from the cell under stated concentrations. The standard state Gibbs energies of relevant species are shown below at the stated conditions.

Solution

Note that two hydrogen ions are generated by the oxidation and two are consumed by the reduction of O₂. The two half-cell reactions are glucose  gluconolactone + 2H⁺ + 2e^–, and O_2(g) + 2H⁺ + 2e^–  H₂O_2(aq). Note that we could use O_2(aq) in the reaction, but that would require an extra calculation using Henry’s law. Since the solution is saturated, we may use the partial pressure in the gas phase where the standard state Gibbs energy is 0. The standard state reduction potential for the glucose reaction is ΔG′° = –427 + 496 = 69 kJ/mol, thus E′° = –ΔG′°/n_eF = –69000/2/96485 = –0.357 V.

For the oxygen reaction, the standard state reduction potential is ΔG′° = –52 = –52 kJ/mol (the Gibbs energy of formation for O_2(g) is 0), thus E′° = –ΔG′°/n_eF = 52,000/2/96485 = 0.269 V. The potential expected from a standard state cell would be E′° = 0.269 + 0.357 = 0.626 V, which is favorable. Let us evaluate E under the proposed conditions. Using the Nernst equation,

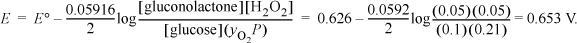
Thus, the cell is favorable. Note that other factors are important before the cell can be implemented, such as the rate that electrons can be produced, which requires preserving the activity (turnover number) of the enzymes. Immobilized enzymes have much slower kinetics compared with free enzymes. Many of the challenges have been summarized by Calabrese Barton, et. al.^a

---

a. Calabrese Barton, S., Gallaway, J., Atanassov, P. 2004. Chem. Rev. 104:4867–4886.

18.13. Nonideal Electrolyte Solutions: Background

To this point in the chapter, we have considered solutions to be ideal or absorbed the nonidealities into the Gibbs energies or equilibrium constants. The representation of nonidealities is important for applications where the concentrations are above approximately 0.01 m. The literature through the 1970s has been largely developed by chemists and a variety of notations and models are used in the literature. More recently, chemical engineers have become actively involved in model development and applications. The remainder of this chapter limits the discussion to the extended Debye-Hückel model and its use as a starting point for more sophisticated models. There are common underlying themes in most of the literature. The use of a standard state in which the dilute activity coefficient goes to unity is common for electrolytes and often for molecular species, though the Lewis-Randall scale is used almost always for water. Due to the prevalent use of molality in literature, coverage of the chemical potential and activity coefficients on that scale is necessary.

As with nonelectrolytes, the chemical potential is the primary property that determines phase equilibria and is independent of the scale used to characterize the value. On the molality scale, the chemical potential of the electrolyte is written in a manner analogous to the Lewis-Randall rule on the mole fraction scale,

where μ_i^o is replaced with  and  is the activity of the component.²⁵ The details of  are subtle as elaborated in Section 18.24. A key consideration is that molality has dimensions of mol/kg that are inconsistent with the (dimensionless) activity and activity coefficient. By defining the standard state at 1 molal, we are implicitly writing , but m_o = 1 mol/kg. We defer the details because most problems are solved by incorporation of  into the Gibbs energy of formation that is commonly tabulated. In other words, the infinite dilution chemical potential is subsumed into the Gibbs energy of formation and reflected in the computation of ΔG_rxn that produces K_a. Then,

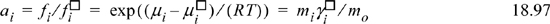
As long as , a_i = m_i. This perspective highlights why the concept is unnecessary to solve problems using K_a at low concentrations as we have done early in the chapter. Because it is common to keep the Lewis-Randall standard state for water, reaction Eqn. 18.14 is written,

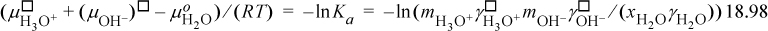
Thus, the activity coefficients and Gibbs energies are related to the equilibrium constant that we have used earlier. Since a solution of pure H⁺ or H₃O⁺ or OH^– cannot exist, we cannot easily use a pure state for either unless it is a hypothetical pure state. However, we can measure the behavior of ions in extremely dilute solutions by various means including spectroscopy and electrochemical cells. Even though measurements are taken at finite concentrations, the behavior can be extrapolated to infinite dilution. To illustrate, suppose the activity of H⁺ can be measured and plotted, as shown in Fig. 18.13. Then extrapolating the measurements to infinite dilution yields an ideal solution that is similar to Henry’s law. Similar to Henry’s law, the activity coefficient goes to unity at infinite dilution. At very dilute concentrations, the molality can usually be approximated by the molarity as we discussed above.

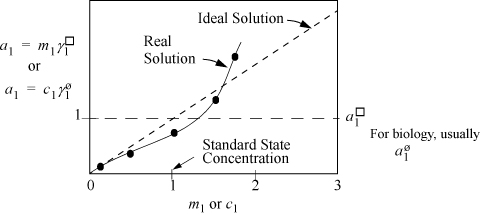
Figure 18.13. Schematic representation of the activity of an ion at low concentration in a binary mixture. The standard states of ions for industrial calculations are typically 1 molal. For biological systems, they are usually 1 molar. The molality and molarity scales are used alternatively, not simultaneously. When using molal concentration, use molal activity. When using molar concentration, use the molar activity scale.

When first working with electrolytes, this standard state can be very confusing. Because the activity coefficient goes to unity at infinite dilution, a common misconception is that the standard state composition is infinitely dilute. However, the standard state composition is 1 molal with a slope taken such that the infinite dilution activity coefficient is unity. An ideal solution on the basis of the standard state follows the dashed line as shown in Fig. 18.13 and extrapolates to higher compositions. Any composition along the dashed line could be taken as the standard state and the activity coefficient would still be unity, but choosing 1 molal as the standard state permits us to (deceptively, but conveniently) drop m_o numerically from many equations. Referring back to non-electrolyte systems, the Henry’s law standard state applies a similar concept, but extrapolates the ideal solution line to the fugacity of the hypothetical pure fluid. Like the discussion here, the slope of the Henry’s law ideal solution is selected such that the infinite dilution value also goes to unity. The difference is that the Henry’s law line is based on fugacity as the y-axis, whereas the electrolyte standard state is based on activity. Like Henry’s law and the Lewis-Randall rule, the activity coefficient quantifies the deviation from the ideal solution line. Readers should refer to Section 18.24 for further clarification of the relations between Henry’s law, the Lewis-Randall rule, and molality/molarity.

18.14. Overview of Model Development

The relation between chemical potentials of the ions and the molal activity coefficients is analogous to nonelectrolytes:

The activity coefficients of the ions are determined from the chemical potentials. The details of model development are beyond the intentions of the overview provided here. Briefly, the Gibbs energy of the solution is equal to the work performed in placing an ion in the solution of other ions. The work is determined from solving Poisson’s equation for electrostatics using various approximations for the charge density,

where r is the radial position, Φ is the electric potential, ρ_±(r) is the charge distribution as a function of radial distance, ε = ε_oD, where ε_o is the permittivity of a vacuum, and D is the dielectric constant. Different models result from different approximations to the charge distribution and the screening. The Extended Debye-Hückel model discussed next is one example of a solution.²⁶ An excellent overview of the approximations and methods of solving the equation is available²⁷ but is beyond the scope intended here. Briefly, once again, the Debye-Hückel approximation results from assuming that the charge distribution follows the low density radial distribution function form

g(r) ~ exp(–u_Coul/kT)

The solvent is considered to be a continuum during the calculation represented by the dielectric constant. Various mathematical approximations are made to develop the solution, and different approximations lead to slightly different approximate formulations used in the literature. The Extended Debye-Hückel model is limited to dilute concentrations, generally below ionic strengths of 0.1 molal, and significant errors result from using the model outside this range. The excess Gibbs energy for the Extended Debye-Hückel theory is²⁸

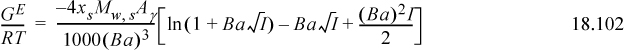
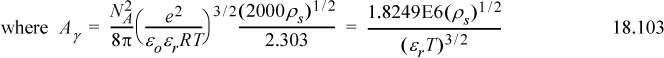
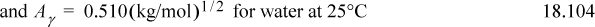
where e = 1.60218E–19 C, ε_o = 8.85419E–12 C² N^-1 m^-2 is the permittivity of vacuum, ε_r is the dielectric constant or relative permittivity of the solvent, R is the gas constant in J/mol-K, T is the temperature in K, ρ_s is the density of the solvent in g/cm³, z_i is the valence of the Coulombic charge on each ion type, and I is the ionic strength which characterizes the overall charges in the charge distribution. The parameter A^γ is not a Helmholtz energy. Dielectric constants for water as a function of temperature are provided in Appendix E. The parameter a represents the average distance of closest approach, which is larger than the ion size due to water hydration which is always present. The term 1/(BI^½) is an approximate distance known as the screening, shielding, or Debye length. It represents the screening of the coulombic potential due to the presence of other ions. A common assumption is Ba = 1 (kg/mol)^½, though in biological systems, Ba = 1.6 (kg/mol)^½.

18.15. The Extended Debye-Hückel Activity Model

Activity Coefficients for Ions

The activity coefficients for ions are obtained by differentiating the excess Gibbs energy of Eqn. 18.102.²⁹ The resultant formula is

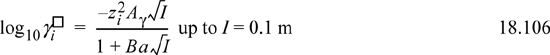
where the constants are defined in Eqns. 18.103–18.105. The ionic strength is calculated based on the actual ion concentrations, which means that for weak electrolytes calculation of I must be repeated when the concentration of ions changes during iterations on concentration. The model predicts activity coefficients that are unity at infinite dilution of ions and decrease to a finite limit at high concentration. Experimentally, activity coefficients usually pass through a minimum at concentrations above 0.1 m, which is not captured by the model. Note that all species with the same charge will have the same activity coefficient values at a given ionic strength. More sophisticated models are available for higher concentrations as we discuss in Section 18.20.

Activity and Osmotic Coefficient for Water

The solvent activity coefficients from the Extended Debye-Hückel theory can be obtained by differentiation of the model for excess Gibbs energy. The result is

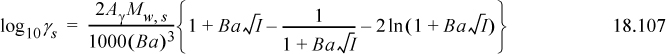
Recall that the activity of the solvent is expressed on the Lewis-Randall standard state. The mole fractions are typically near unity, and thus many significant digits are required to characterize activity coefficients of solvent. Commonly the activity of the solvent is expressed in terms of the “practical” osmotic coefficient, Φ,

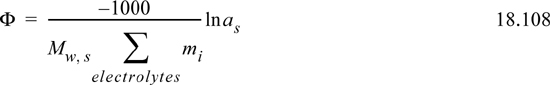
In literature, activities of ions are often measured indirectly by measuring or controlling the partial pressure (isopiestic method) of water above the solution and then reporting the osmotic coefficient. The results are very sensitive to whether complete dissociation is assumed for activity calculation and in the summation in the denominator. Readers must pay careful attention to the assumptions applied in the experimental interpretation. The osmotic pressure can be converted to the ion activity using the Gibbs-Duhem equation to obtain the mean ionic activity coefficient described in Section 18.19. The osmotic coefficient approaches 1 at infinite dilution of ions. The osmotic coefficient is related to the osmotic pressure,

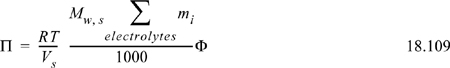
Nonidealities for Nonelectrolyte Solutes

When nonelectrolytes exist in solution with electrolytes, such as with acetic acid, the undissociated acetic acid is typically treated with a molal standard state with the corresponding unity infinite dilution activity coefficient. To fit experimental data, the activity coefficient can be represented as  where b is a constant fitted empirically. While this does not satisfy the Gibbs-Duhem equation, it is a common model.

18.16. Gibbs Energies for Electrolytes

In Chapter 17, we determined K_a from the Gibbs energy of formation. However, we also noted that occasionally results are summarized in terms of a temperature-dependent K_a. Treatment of the model using K_a requires less thermodynamic information, and it is quite common for electrolytes. Tabulating in terms of Gibbs energies requires consistency with a large database that is tedious to maintain. Such data bases are available for common ions only.

The Gibbs energy of reaction can be represented by

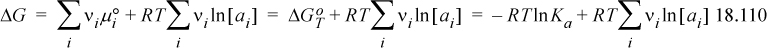
Writing a completely general notation is difficult because different standard states are often used for different components. For example, we have already discussed using  for cations and similar notation for anions. Writing a general sum is clumsy because of the different standard states used for components, so we leave the generic superscript ° and expect that readers apply the appropriate standard states.

Two key steps in understanding the tables for Gibbs energies are to consider the dissociation constant of water, and the selection of zero as the Gibbs energy of formation for H⁺. These steps and choices become clearer in upcoming descriptions. In Chapter 17, we introduced the use of Gibbs energy of the reaction as

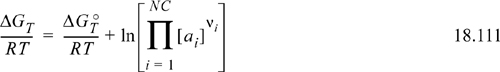
Consider again the dissociation constant for water, as shown in Eqn. 18.4. The equilibrium constant for this reaction at 298.15 K is well known as K_a = 10^–14. The Gibbs energy of the reaction is thus:

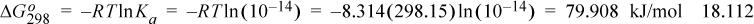
Now consider that the Gibbs energy of the reaction can be calculated by the Gibbs energies of formation at 298.15 K using the value from Eqn 18.112:

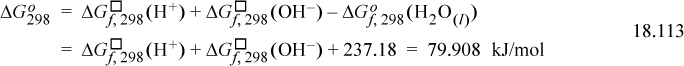
Note that, like the chemical potentials, writing a general notation for  is slightly imprecise and we use the default ° superscript, expecting readers to insert the ion standard state for ions. Note that the standard state Gibbs energy for pure water at 298.15 K has been inserted from the tables for nonelectrolytes. This detail makes an important connection with the standard tables for all other molecular components, and thus the values from the usual tables can be applied when compounds appear in reactions with electrolytes, as long as this convention is used.

Looking at Eqn. 18.113, two values are unknown, both  and . The dilemma is resolved with the arbitrary choice at 298.15 K and 1 bar:

This convention then determines the value

With these values, the remainder of the tables can be developed. Other acid reactions involving H⁺ can then be characterized based on the degree of dissociation and the above standard selection of . For example, the value of  can be determined by the dissociation behavior of HCl. Once the Gibbs energy of Cl^– can be determined the dissociation of NaCl will lead to the Gibbs energy of Na⁺. The remainder of the tables are developed using similar calculations.

Strategy for Using Gibbs Energies

There is important perspective regarding tabulation of standard state Gibbs energies. Have you considered how scientists created the tables for ? Scientists used experimental equilibrium concentration measurements with models to calculate a_i, and then inserted them into the equilibrium relation:

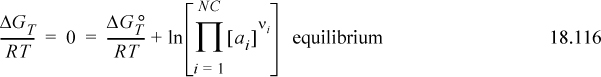
Experiments were performed where  (or ) was known for all but one of the species. Then the value of  for the species was determined from the experiment by difference. Calculations from multiple investigators using different reactions refined the values that we use from the tables today. When we solve an applied problem, we are using the equation in the opposite direction: looking up  (and ) and using models of a_i to determine concentrations. Calculations are reliable as long as a_i’s are calculated using methods consistent with the standard state  and .

The steps to solving a problem usually involve reverting the procedures used to develop the tables. Tables are used to calculate  (or ) from standard state. Temperature and pressure corrections are applied to determine ΔG_T,  In K and then selecting methods to calculate a_i consistent with the standard state. Concentrations are thus determined from the activity, often assuming ideal solutions. Frequently, the Gibbs energies of individual species are not calculated, or are not available. Rather, scientists report the values of K_a as used in Example 18.4. A reliable database of Gibbs energies is available as documented in footnote 13 of this chapter.