The terms strong and weak are used when referring to acids and bases in a manner similar to salts. The terms do not imply anything directly about pH. Rather, like other electrolytes, they refer to a compound’s degree of dissociation. When the dissociation constant is extremely large the acid/base is considered strong; when dissociation is incomplete the acid/base is considered weak.
Strong Acids/Bases and the Leveling Effect
The magnitude of the dissociation constant (or the associated Gibbs energy of dissociation) determines whether an acid/base is strong or weak. An acid is a proton source and reacts with the solvent (usually water) to create an increased activity of [H+] or [H3O+]; for example, AcOH in Eqn. 18.15 is a proton donor and an acid. HCl is a strong acid and dissociates totally at common concentrations to form H3O+ (denoted as H+) and Cl–. A base acts as a proton sink, reacting with water to withdraw a proton and increase the hydroxide activity, as shown by the reaction of the weak base ammonia with water,
Hydroxides are also common strong bases, such as NaOH or Ca(OH)2. These strong bases are a direct source of hydroxide because when they dissociate the [OH–] must be high to balance the positive cation charges in solution.
The strength of an acid or base is determined by the solvent, which governs the degree of dissociation/reaction. Table 18.2 illustrates acid/base strength. Strong acids are to the upper left. Strong bases are to the lower right. Weak acids are in the left column below H3O+. Weak bases are in the right column above OH–. The reaction of H3O+ with water may initially look like little has happened: 
. All acids in the left column above H3O+ are equally strong when they are dilute in water because the protons released from the acid immediately react with H2O to give hydronium ions. Thus, the strongest acid in water is H3O+ and any stronger acids are leveled to be the same strength. In an analogous way, OH– is the strongest base that can exist in water. Any other proton sinks added to solution from stronger bases react immediately with water to give OH–. (Often these reactions are violent and superbases must be handled with care near water.) Strong bases are leveled by water and do not produce a stronger base solution than an equivalent concentration of NaOH. Sometimes organic chemists use strong acids or strong bases in non-aqueous solvents to overcome the leveling effect.
Table 18.2. Reference Table for Relative Acid and Base Strengths at 25°C Based on pKa,water = –13.995. pKb = 13.995 – pKa
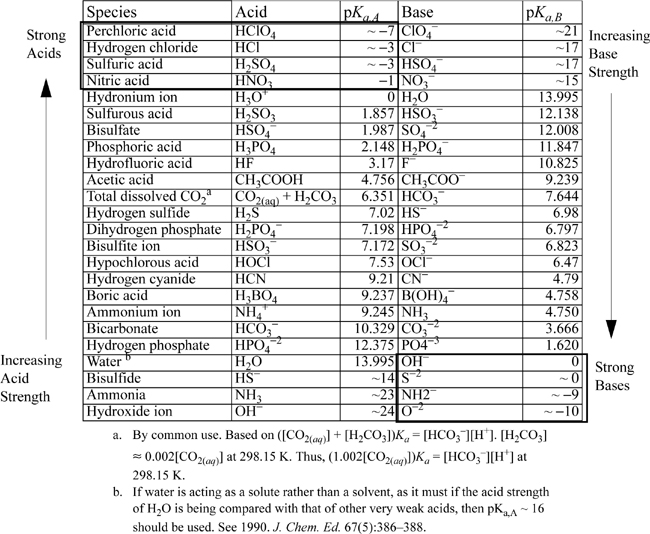
Each acid in the left column in the table has a conjuate base in the right column. Similarly, each base in the right column has a conjugate acid in the left column. Strong acids have weak conjugate bases, and strong bases have weak conjugate acids.
Strong Acids
Consider the behavior of HCl in solution at an apparent molarity of CA. The behavior is characterized by the dissociation of HCl (essentially complete) and the dissociation of water. Further, a charge balance must exist in solution, yielding the following conditions
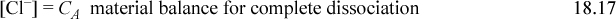
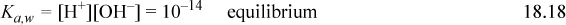
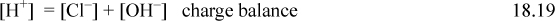
The next step is important and we use it throughout our calculations. Though trivial here, later we find it important to combine the material balance and charge balance to arrive at a balance known as the proton condition. The principle is to insert the known constants from the problem statement, which often cancel to leave the intermediate and smaller concentrations. In this case no terms drop out, but the proton condition becomes
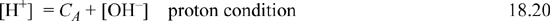
Think about the size of the [H+] and [OH–] and how they are coupled to Ka,w. Suppose that CA = 10–2 mol/L. Then, by the coupling of the equilibrium and charge balance, because HCl is an acid, we expect [OH–] < 10–7 mol/L by Eqn. 18.10, thus [OH–] << [Cl–] = 10–2 mol/L. The charge balance involves terms that are very different in size. Now, when CA > 10-6.5, it is a good approximation to ignore [OH–] and we can calculate pH = pCA. At low acid concentrations below about 10-6.5, we must insert the dissociation constant for water into the charge balance, to obtain [H+] = CA + Ka,w/[H+] and solve the resultant quadratic equation for [H+]. The behavior of strong acids is plotted in Fig. 18.3. Note that a good approximation for the strong acid curve on this log-log plot is a diagonal line with slope –1 running from (0,0) through (7, –7). It is an excellent approximation from (0,0) through (6.5,–6.5).
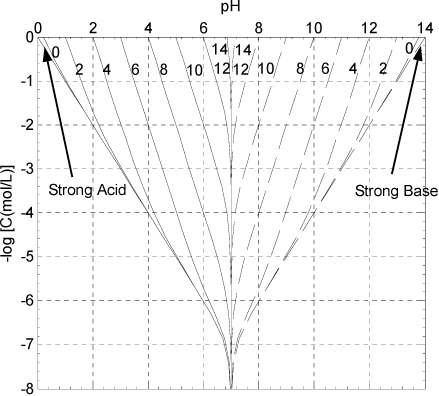
Figure 18.3. Flood diagram showing the behavior of strong monoprotic acids, weak monoprotic acids, salts of weak monoprotic bases, and strong monovalent bases.
Strong Bases
Consider a strong monovalent base, such as [OH–]. In a solution of apparent molarity CB of NaOH the constraints are
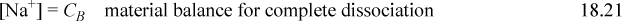
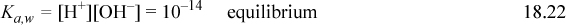
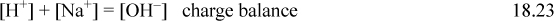
Combining the material balance and charge balance results in the proton condition
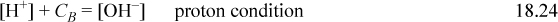
When CB > 10-6.5, it will be a good approximation to ignore [H+] and we can calculate pH = 14 – pCB. At low concentrations, the quadratic equation becomes [H+] + CB = Ka,w/[H+]. As evident in Fig. 18.3, a good approximation for the strong base curve on this log-log plot is a diagonal line with slope 1 running from (7,–7) through (14, 0).
Weak Monoprotic Acids
Consider a weak monoprotic acid such as acetic acid, pKa,A = 4.7. We denote as the undissociated acid as HA. The weak acid requires an additional dissociation reaction because it is incomplete. The material balance is written including the acid HA and conjugate base A–, because the acid is only partially dissociated. The acid equilibrium constant is required to quantify the dissociation.
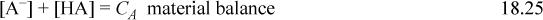
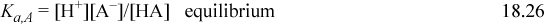
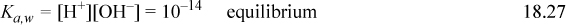
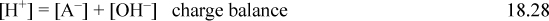
The rigorous solution to pH at a given concentration can be obtained from Eqn. 18.26 by eliminating [HA] and [A–] in terms of [H+] and [OH–] and then eliminating [OH–] using [OH–] = Kw/ [H+], resulting in a cubic equation,
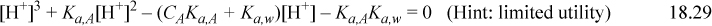
Solutions of the cubic for various pKa,A values and concentrations are shown in the solid lines on the left side of Fig. 18.3. The graph can serve as a useful guide for monoprotic weak acids, but is only applicable for the charge balance of Eqn. 18.28 when no other ions are present. Rather than solving the cubic, or becoming too reliant on the graph, real problems usually involve other ions, and thus the Flood diagram and cubic have limited utility. Instead, we utilize two equations that relate [A–] and [HA] to CA and [H+] and are always applicable, even when other ions are present. Combining the material balance with Eqn. 18.26 to eliminate [A–] results in Ka,A = [H+](CA – [HA])/[HA] which becomes
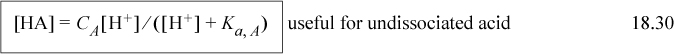
Combining the material balance with Eqn. 18.26 to eliminate [HA] results in Ka,A = [H+][A–]/(CA – [A–]) which becomes
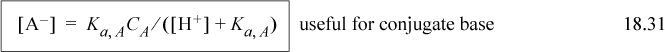
Note that the denominators of the last two equations are the same and we need to know the pH to solve for the concentrations. Example 18.4 shows how these equations are useful for problem solving.
Weak Monoprotic Bases
Consider a weak monovalent base such as acetate ion, denoted as A–, pKa,B = 9.3, which might be added to solution as sodium acetate. The sodium acetate dissociates completely, making it a strong electrolyte, but the acetate equilibrates with water to form undissociated acid (HA) and hydroxide, 
, so sodium acetate is called a weak base. The material balance is written for the cation in this case as well as the two forms of A, and the governing equations are:
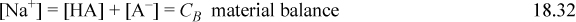
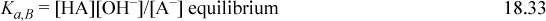
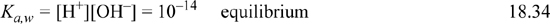
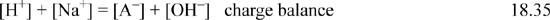
In an analogous way to treating weak acids, the material balance and charge balance are combined to eliminate [HA] and [A–] in terms of [H+] and [OH–]. Then the dissociation constant of water is used to eliminate [OH–], resulting in
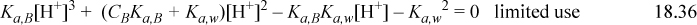
The same equation results from a weak neutral base with capacity for one ion, such as ammonia. Note, however, for ammonia that the base NH3 is neutral and the conjugate acid NH4+ is charged, but when the charge balance is modified and the same method is used, Eqn. 18.36 results. As with a weak acid, the pH values at various base concentrations have been plotted in Fig. 18.3. As with weak acids, the charge balance that leads to the cubic equation does not hold when other ions are present. However, we can solve problems using Eqns. 18.30 and 18.31. Thus, we develop a single method of solution regardless of whether acid or base is added to water. Note that
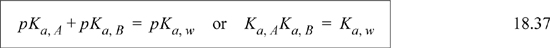
As an example, consider the fluconazole shown in Fig. 18.4. This is a drug used for treating fungal infections. Fluconazole is a base that is protonated in water, depending on pH:
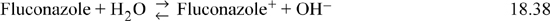
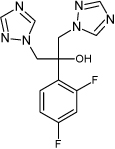
Figure 18.4. Structure of Fluconazole.
By lowering the pH, the [OH–] is lowered, driving the reaction to the right. At high pH values, the reaction shifts to the left, as we show in Example 18.4. The equilibrium shift affects solubility as we consider in Example 18.8 on page 726.
Example 18.4. Dissociation of fluconazole
Fluconazole is a drug used for treating fungal infections. Behavior of drugs at various pH conditions is important because the stomach system is at low pH, but the intestinal system has a higher pH. Thus, models for the dissociation and solubility are desirable. Fluconazole equilibrium written as Eqn 18.38 can be modeled with the expression
where fluconazole and its ion and the hydroxyl are on the molality scale and water is on the Lewis-Randall scale. Determine the percentage of fluconazole dissociated at pH 7 and pH 1.5 when the apparent amount of fluconazole in aqueous solution is 1.5E-3m. The molecular weight of fluconazole is 306.27. Assume ideal solutions.
Solution
First consider the chemical reaction to identify the acid and base. In this case, the fluconazole is the base and the fluconazole+ is the acid. Therefore Eqn. 18.39 represents Ka,B. As with this example, it is common in the literature that acids and bases are not explicitly identified, and recognition is an important step in the solution. We can rewrite the reaction in the acid form as,
Fluconazole+ + H2O 
Fluconazole + H3O+
(We adopt this approach of writing reactions in the acid form as a standard method, as further implemented in Section 18.9 below.) For Eqn. 18.39, the equilibrium constant at 298.15 K is Ka,B = 6.181E-13, or Ka,A = 10–14/6.181E-13 = 0.01617, or pKa,A = 1.79. Therefore, the fluconazole is predominately protonated below pH = 1.8 and largely neutral above. The calculations should bear out this rule of thumb.
At pH = 7 we have from Eqn. 18.30,
[Fluc+] = Cfluc[H+] / ([H+] + Ka,A) = 1.5E-3m(10–7)/(10–7 + 0.01617) = 9.27E-9m. Therefore, [Fluc] = 1.5E-3m, and the fraction protonated is 9.27E-9/(1.5E-3)·100% = 0% (trace).
At pH = 1.5, the system is near the pKa,A and both terms are important in the denominator, [Fluc+] = Cfluc[H+] / ([H+] + Ka,A) = 1.5E-3m(10–1.5)/(10–1.5 + 0.01617) = 9.9E-4m. Thus, [Fluc] = 1.5E-3m – 9.9E-4m = 5.1E-4m. The concentration of protonated species is higher, as expected. The fraction protonated is 9.9E-4/(1.5E-3)·100% = 66%.
Perspectives on Calculations
Calculations for electrolyte systems can be challenging to converge because the concentrations of important species vary by several orders of magnitude. Each pH unit is an order of magnitude; thus, at pH 2 compared to pH 7 the [H+] is five orders of magnitude larger. Calculations using Excel Solver are insensitive to the latter condition if the Solver tolerance is set to 1E-3! Also, issues may occur if iterating on values near zero because the concentration of 1E-3 can easily jump to a negative value on the next iteration if not constrained. Iterations can also converge slowly for some situations.12 Because charges are involved, the net charge in a solution must be zero; a charge balance is required when iterating on concentrations. However, a charge balance often involves adding terms that are different by orders of magnitude. There are several general recommendations.
1. Develop a good initial guess using techniques that we discuss below. The pKa,A represents the pH condition where the reaction coordinate will be 50% between acid and conjugate base and thus their concentrations will be equal.
2. Constrain concentrations to be positive or use logarithms of concentrations for iterations when using automated equation solvers.
The pKa,A represents the pH condition where the reaction coordinate will be 50% between acid and conjugate base, and thus their concentrations will be equal.
3. Set the convergence criteria in Solver or optimization routine to an extremely small number (1E-30) and the number of iterations to a high number.
4. Check results to ensure convergence, especially if the specified number of iterations is reached.
How does one generate a good first guess when the concentrations differ by orders of magnitude? The best way to generate a good first guess is to use a Sillèn diagram. Sillèn diagrams, originally developed by Swedish chemist Lars Gunnar Sillèn in the 1950s, are quick to sketch. The next section discusses how to construct and use a Sillèn diagram. Often the results from the Sillèn are sufficiently accurate for routine practical applications or as first estimates for more detailed calculations using activity coefficients.
Other important aspects of the initial examples include the standard states, concentration units, and composition independence of K. The typical convention used for standard states of charged species is similar to Henry’s law, but subtly different. Without belaboring the details until later in the chapter, the activity coefficients for the charged species are unity at infinite dilution, and we will disregard the activity coefficients for the introductory examples. The corrections are typically small when the concentrations of ions (measured by the ionic strength) is low, less than approximately 10–2 m. We will use this approximation at even higher concentrations to develop problem-solving strategies. The reader should be cautioned that the activity coefficients for charged species can become large rapidly and can be very large, but typically above 5m. A good understanding of the standard state for water and uncharged solute species is also important. The standard states for water and uncharged solutes are different from that used for charged species. Uncharged solutes, such as molecular acids and bases, like acetic acid or ammonia, are treated with Henry’s law. This shares a similarity to the treatment of charged species, because the activity coefficients are unity. Water, on the other hand, is treated relative to the Lewis-Randall standard state of pure water. Because the water concentration on a mole fraction basis is nearly one, it will be sufficient to approximate the activity coefficient of water as one and the activity of water will be approximately one. In summary, we extend the concepts of using unsymmetric standard states introduced in Chapter 11.
Ions are treated with a molal standard state. Aqueous molecular solutes are treated with Henry’s law. Water is treated with the Lewis-Randall rule.
Another important approximation is that we use molar concentration rather than molality to work the examples early in the chapter. This follows the conventions used in introductory chemistry, and, as shown in Table 18.1, can be a good approximation at low concentrations. Technically, the units should be molality for the electrolyte species, and certainly the examples can be reworked with those units, but use of molality requires more unit conversions with little pedagogical advantage. The later examples in the chapter use molality to demonstrate the more rigorous approach.
Temperature, Pressure, and Composition Effects on K
Initially, the discussions and examples provide values for equilibrium constants. Commonly in introductory chemistry texts values are provided for 298.15 K, though the designation is often omitted in those texts. The values of Ka change with temperature as with any reactive system.
In Chapter 17, the equilibrium constant did not depend on pressure. This is not the case for electrolytes when the typical electrolyte standard state is used for ions, though it is common to neglect it as a first approximation. When an ion is dissolved in water at infinite dilution, the hydrogen bonding is disrupted resulting in a pressure-dependence for the infinite-dilution standard state. We do not develop the details further in this text, but readers should consult advanced texts or handbooks when working at high pressures.13
There are two conventions to correct for solution nonidealities. Extending the concepts of Chapter 17, the most rigorous method of including solution nonidealities is to use activity coefficients as we show later. However, another method used in the literature is to determine the dependence of K = Ka / Kγ on ionic strength of the solution, and then proceed with calculations using K rather than Ka. This is possible because to the first approximation the activity coefficients depend on charge and ionic strength and are independent of species (as we show in Section 18.15). Therefore, when working with values from the literature, some care is necessary to discern if the authors’ values for K are at the standard states or if they are corrected for ionic strength. When the dependence of ionic strength is included and K is substituted for Ka, the methods developed below can be used directly by replacing Ka with K in the calculations.
18.9. Sillèn Diagram Solution Method
Monoprotic Acids and Bases
Seven main steps are necessary to solve electrolyte problems using a Sillèn diagram (cf. Fig. 18.5), which is similar to a Flood diagram. We summarize the steps and then work an example for sodium acetate. Skim the procedure initially, and then follow closely with Example 18.5.
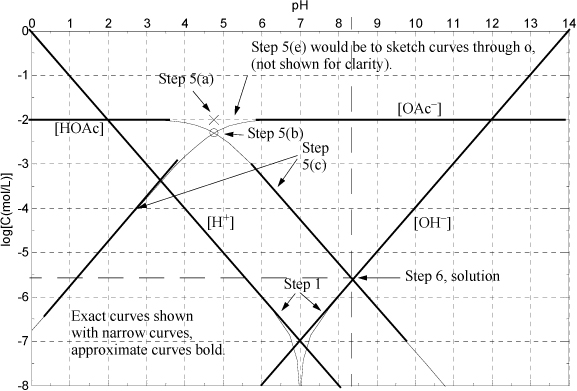
Figure 18.5. Sillèn plot for Example 18.5, acetate with an overall concentration 0.01 M.
1. Create a coordinate system like the Flood diagram. (A template is available on the textbook web site.) Draw straight lines for the strong acid and strong base lines. The detail of the taper at pH = 7 should be ignored, and cross the lines. Note that the sum of the two lines is always –14 on the log scale and represents the ion product for water. Label these lines [H+] (left) and [OH–] (right).
Some rules of thumb are helpful for plotting on common logarithmic coordinates. Note that when [B] = 2[A], the ordinate of [B] on a log10 scale is 0.3 units higher than [A]. Likewise, when [B] = 0.5[A], then the [B] ordinate will be 0.3 units lower. A factor of 5 is 0.7 units. And of course a factor of 10 is one unit. For convenience the pairs of (linear factor, log10 translation) are (2, 0.3), (3, 0.47), (4, 0.6), (5, 0.7), (6, 0.78), (7, 0.85), (8, 0.9), (9, 0.95), (10, 1).
2. Write the material balance for the dissociating species to relate the apparent species to the species in solution; for example, Eqn. 18.32.
3. Write the equilibria relations using the dissociation constants for weak acids or bases. If the acid/base is strong it will completely dissociate, and thus the relation is not needed. Always write the reactions in the acid form (even if bases are involved); for example, Eqn. 18.26 for acetate or acetic acid. Write the dissociation reaction for water. Using the acid form provides a consistent solution strategy, but is not theoretically required.
4. Write the electroneutrality constraint.
5. Sketch Eqns. 18.30 and 18.31 without calculations on the diagram using these steps. (See the example.) The steps are: (a) create a system point at CA (or CB) and pKa,A; the procedure always uses pKa,A, even for bases; (b) create an acid/base intersection point at (pKa,A, logCA – 0.3). (The value of 0.3 represents a decrease of 50% in the concentration, which is where the acid and base concentrations will match.); (c) sketch diagonal lines with slope +1 and –1 (parallel to the H+ and OH– lines) below CA that project through the system point but extend downwards starting about logCA – 1; (d) draw horizontal lines on either side of the system point leaving a gap of approximately 1 pH unit on either side of the system point and label the line on the left (low pH) as the acid and the line to the right (high pH) as the base; (e) connect the sloping lines with the horizontal lines with smooth curves that pass through the acid/base intersection point.
6. Decide which concentrations are largest and which are least significant. Let Ci be the apparent concentration. The goal is to simplify the balances and provide a good guess for true concentrations. This is almost always done by converting the charge balance to a proton condition by inserting the mass balance to eliminate terms that are largest and leave smaller terms that are more similar in magnitude. Use the diagram as a guide to decide which concentrations are insignificant in the pH range expected. The goal is to use the proton condition to identify the intersection of the positive and negative charges of the proton condition. Unless some of the diagonal curves are very close to each other this will be easy. There can be various proton conditions that are equally valid when many ions are present at similar concentrations. Hints: Remember that each unit on the log scale is an order of magnitude. Acids by themselves result in pH < 7; bases alone result in pH > 7; salts of a strong acid and weak base (e.g., NH4+Cl–) are acidic; salts of a weak acid and strong base (e.g., NaOAc) are basic.
7. Check the result. The results can be checked by iterating on charge balance pH by inserting Eqns. 18.30 and 18.31 or the analogs.
Example 18.5. Sillèn diagram for HOAc and NaOAc
Sodium acetate, NaOAc, is dissolved in water at an apparent concentration of CB = 10-2 mol/L. Construct a Sillèn diagram and estimate the pH. For acetic acid, pKa,A = 4.76 at room temperature in dilute solutions.
Solution
Here we replace the generic A– with OAc– to denote acetate. The Sillèn diagram is presented in Fig. 18.5. The approximate solution (thick lines) is shown below superimposed on the exact equations (thin lines).
Step 1: The lines for [H+] and [OH–] have been drawn and labeled in the figure.
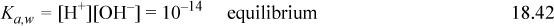
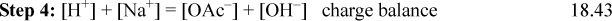
Step 5: See the diagram labels denoting steps 5(a) and 5(b). Referring to the procedure above indicates the system point (x) should be at CB and pKa,A. On the diagram below, use a straight edge to verify that the lines for step 5(c) extrapolate through the x from step 5(a). Note that the curves for step 5(e) are not shaded for clarity, but it is obvious that the curves could be easily drawn through o. Recall that step 5 plots Eqns. 18.30 and 18.31 without calculations.
Step 6: Develop the proton condition. This step is very important and can be the most confusing. It is best understood by using equations together with the diagram. Since we have dissolved the salt of a weak acid and strong base, we expect the pH to be above 7. Looking at the diagram in this range, [OAc–] >> [HOAc] and we will be unable to reliably calculate [HOAc] = CB – [OAc–] with the material balance because the last two terms are nearly equal. Let us use the material balance to eliminate the large terms [Na+] and [OAc–] from the charge balance. Note that we can replace [Na+] with CB and [OAc–] = CB – [HOAc]. This causes all the largest terms to drop from the charge balance, giving
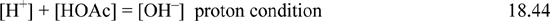
Eqns. 18.40–18.43 are now all condensed to using Eqn. 18.44 with the graph, looking for where the proton condition is satisfied. Looking at the lines on the graph where pH > 7, it is obvious that [HOAc] is almost three orders of magnitude larger than [H+] above pH = 5. Thus, the left side of the proton condition becomes [HOAc] + [H+] = [HOAc] + … where … denotes a very small number. The proton condition becomes [HOAc] + … = [OH–], and the solution is given for practical purposes by the intersection of the [HOAc] curve with the [OH–] curve as shown in the diagram. The approximate concentrations are
pH = 8.4, pOH = 14 – 8.4 = 5.6, [HOAc] = 10–5.6, [Na+] =[OAc–] = 10–2
Step 7: The proton condition is in terms of Eqns. 18.27 and 18.30, and avoiding taking differences, [OH–] = 10-14/[H+] = [H+] + [HOAc] = [H+] + CA[H+] / ([H+] + Ka.A)
Rearranging for successive substitution on [H+], and inserting the initial guess of pH = 8.4, iterate on the highest power of [H+],
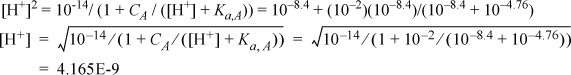
pH = 8.38. Plugging this back in results in no further changes. Recall that if successive substitution results in divergence rather than convergence, that the equation needs to be rearranged. See Appendix A, Section A.4.
This example has demonstrated that a relatively complex problem can be solved rapidly with a quick sketch. A key simplification used in this introductory example was that [H+] << [HOAc]. Do not generalize this approximation. If the same problem is repeated with CB = 10–4 mol/L, this translates the lines for [HOAc] and [OAc–] downwards two orders of magnitude and the lines for [H+] and [HOAc] become very close. The approximation [H+] << [HOAc] is not valid then. Instead, the left side of the proton condition, [H+] + [HOAc], can be calculated at a selected point from the two lines. The [H+] + [HOAc] sum becomes a line through this point with the same slope as the individual lines. The answer is where this “summed” line crosses [OH–].
A remarkable feature of this solution technique is that the solution to the four simultaneous equations did not require sophisticated algebra or a cubic equation. As an exercise, consider a solution of acetic acid, CA = 10–2 mol/L. The diagram is the same as used above. However, the material balance and proton condition are different. Use the diagram to show that the pH = 3.35 approximately.
Polyprotic Acids and Bases
The phosphoric system (H3PO4, H2PO4–, HPO42–, PO43–) and the CO2 (CO2, HCO3–, CO32–) systems are important for both biology and environmental applications. Succinic acid, a dicarboxylic acid produced by fermentation, is expected to become more widely produced via fermentation in future years, typically as a salt. Amino acids, the building blocks for proteins, combine a basic amine and a carboxylic acid on the same molecule. Let us begin by considering the nonvolatile phosphate system.
Phosphate System
The equilibria can be written (using all acid equilibrium constants, but without the A subscript for convenience),
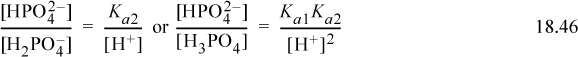
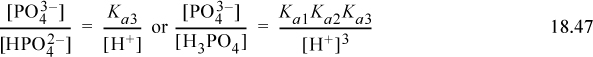
The material balance on phosphorous is
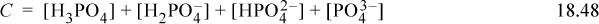
Defining a variable αi to denote the fraction of each species relative to the total phosphate concentration where the subscript denotes the number of protons,
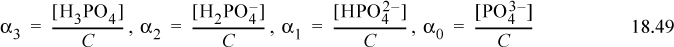
Dividing the material balance by [H3PO4], we find the reciprocal of α3,
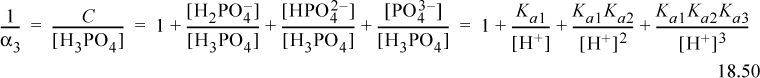
Inverting and simplifying,
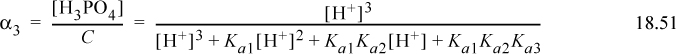
Then α2 as the fraction of acid with three protons is
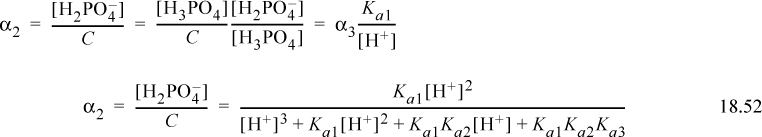
Recognizing the recurring relation between the fractions, the arguments for one and no protons are
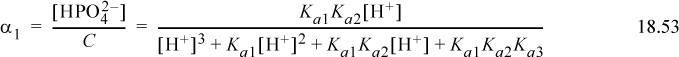
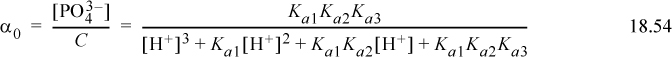
The Sillèn diagram for the phosphate system is slightly more complicated than a monoprotic system, but can still be quickly drawn by hand. The concentration of each species i can rigorously be calculated at each pH by αiC where αi is calculated from Eqns. 18.51–18.54. The exact concentrations are shown in Fig. 18.6 for C = 10–2 mol/L. The upper part of the Sillèn diagram is analogous to the monoprotic diagram. The difference is that the slopes change to +2 or –2 when the species concentration crosses the pKa,A for a neighboring dissociation. The curve passes through a y coordinate approximately 0.3 “log10 units” below the point where the upper extrapolated line crosses the neighboring pKa,A. Though not apparent from this diagram, at very low concentrations when the species concentration crosses additional pKa,A values, the slope increments (decrements) again by one.
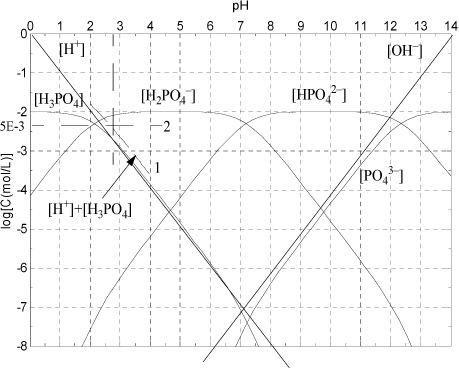
Figure 18.6. Phosphoric system at C = 10-2 mol/L discussed in Example 18.6.
Example 18.6. Phosphate salt and strong acid
A solution of NaH2PO4 and HCl is prepared such that the total phosphorous concentration is 1E-2 M and the total Cl concentration is 5E-3M. Calculate the pH and concentrations of species present.
Solution
Begin a problem with multiple ions with the material balance. The material balances on the sodium, chloride, and phosphate are:
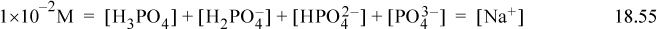
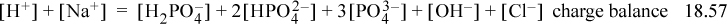
Note the coefficients on the ions in the charge balance. The Sillèn diagram for the phosphate system is shown below. It may seem daunting that so many species are present, but when you look at the Sillèn diagram, notice that only two phosphate species at a time are important at any pH range. This occurs because the pKa,A values are well separated. The curves are drawn with the exact relations, but can be quickly sketched. Practice the sketch using the rules given above and compare with Fig. 18.6.
Steps 1-5 of the procedure have already been executed.
Step 6. The proton condition is developed by eliminating [Na+] and [Cl–] using the material balances since they are both known constants. The material balance for phosphate is also inserted, resulting in
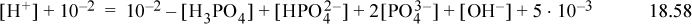
which becomes
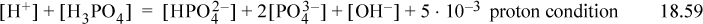
Understanding where to find the solution requires some thought and reasoning rather than a direct numerical manipulation. Both terms on the left side of the proton condition are almost equal at 2.5 < pH < 7. The values are added on the short dashed line marked “1” (since they are virtually equal in most of the range, the sum is double, or about 0.3 units higher on the log10 scale). Note that [H2PO4–] does not appear in the proton condition. On the right-hand side, the term 5E-3 dominates at pH < 6. Solutions at high pH are impossible because the decreasing right-hand side is too small to balance the value of 5E-3 plus increasing concentrations of the negative phosphate and hydroxide ions in the proton condition. Therefore, the solution must be a low pH where the concentration of negative phosphate and hydroxide ions in the proton condition are small. The solution occurs where [H+] + [H3PO4] = 5E-3 (the line marked “2”), and pH = 2.6. The approximate concentrations from the diagram are [H+] = [H3PO4] = 2.5E-3. Eqn. 18.45 simplifies to [H2PO4–] = Ka1 = 10–2.15, [HPO42–] = 10–6.5, [Na+] = 1E-2, [Cl–] = 5E-3.
Step 7. The detailed calculations are often tedious. Inserting Eqn. 18.51 into the proton condition, where the first three terms on the right side are negligible,
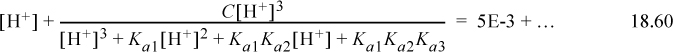
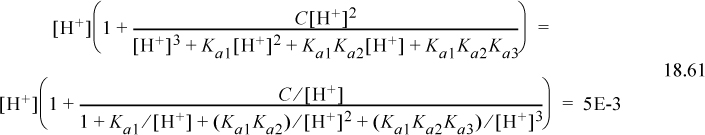
Inserting the initial guess,
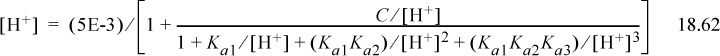
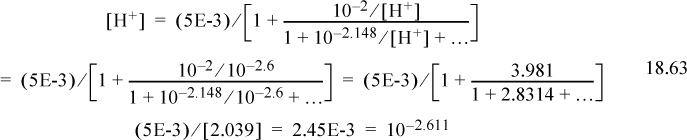
Repeating the iteration results in [H+] = 2.44E-3, pH = 2.613. Note how close we were with the graphical value of pH = 2.6.
Amino Acids
Amino acids are the fundamental building blocks from which all proteins are built. DNA encodes the formulas used to assemble 22 standard amino acids into the multitudes of proteins. Proteins with specific catalytic functions are called enzymes. Amino acids include at least one carboxylic acid group and one amine group. The 20 amino acids summarized in Fig. 18.7 are encoded in the universal genetic code. Together with selenocysteine and pyrrolysine which are encoded in special situations, the 22 amino acids link together to provide the functionalities required for biological life by use of various side chains. When biological machinery assembles amino acids into proteins, a carboxylic acid from one amino acid is covalently bonded to the amine on the next amino acid. One end of any protein backbone is an amine and the other end is a carboxylic acid. Note that some side chains in Fig. 18.7 include acidic and basic side chains. These acidic and basic side chains lead to charges on proteins, which change as a function of pH. Since biological systems usually have buffered pH near 7, which is above the pKa,A for the carboxylic acids, those groups are in the conjugate base form, leading to negative charges on the side chains. Similarly, basic groups below the pKa,A are protonated. For example, serum albumin, a globular (round) blood protein, has negative charges on the surface at physiological pH. At physiological pH, it has an intrinsic charge of -17 and binds 6 monovalent anions giving a total net charge of –23. At low pH, the intrinsic charge becomes positive and the protein binds more anions. Hence the charge and binding change with pH.14 Serum albumin is critical for controlling the intravascular hydrostatic pressure by regulating the osmotic pressure. About half of the osmotic pressure is controlled by Donnan equilibria, as described on page 725. Other proteins have a larger number of basic side groups than acidic groups. The basic side chains are protonated at neutral pH, contributing a positive charge.
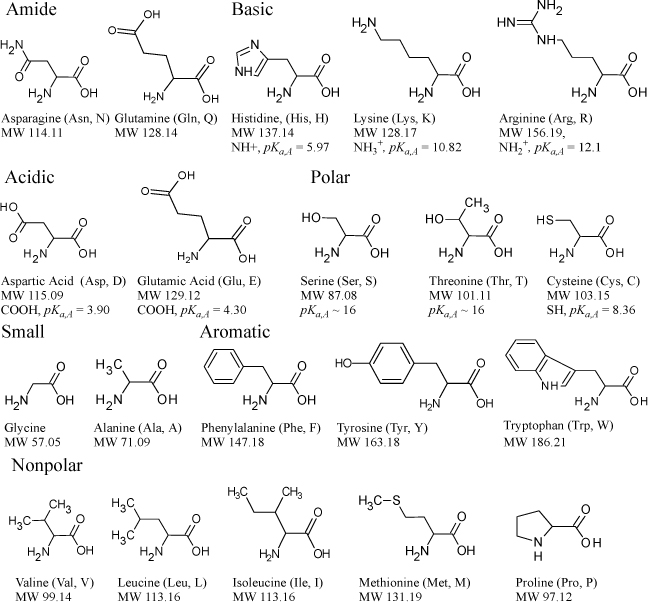
Figure 18.7. Summary of 20 amino acids encoded by the universal genetic code. The amine and carboxylic groups on the bottom of each molecule are where the amino acid is linked into the biomolecule. The acidic and basic side chains are shown uncharged.
Glycine
Glycine is the simplest amino acid. The side chain is simply a hydrogen; that is, there is no side chain. For glycine, pKa,A1 = 2.35 for the carboxylic acid and pKa,A2 = 9.78 for the amine. Thus, the amino acids combine the concepts of acids and bases with the concepts of a polyprotic system. The species at various pH values and nomenclature are shown in Fig. 18.8. Note that the species at neutral pH has a net charge of zero, but includes a positive and negative charge. Such a molecule with both positive and negative charges is called a zwitterion (German for “hybrid ion”). This combination of positive and negative charges results in large dipole moments for biological molecules at neutral pH. The relevant equilibria are (written using acid dissociation constants, but omitting the A subscript):
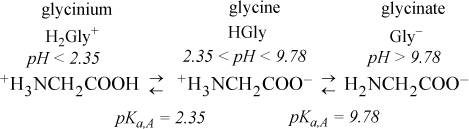
Figure 18.8. Dominant species for glycine at various pH levels. pKa,A = 2.35 for the carboxylic acid and pKa,A = 9.78 for NH3+. The top line shows the nomenclature and the second line shows abbreviations.
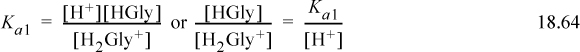
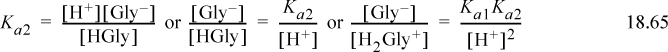
Example 18.7. Distribution of species in glycine solution
a. Calculate the pH of a 0.1 M solution of glycine.
b. What is the distribution of species for glycine at a physiological pH of 7.4?
Solution
A Sillèn diagram for glycine (Fig. 18.9) is sketched by the standard procedures.
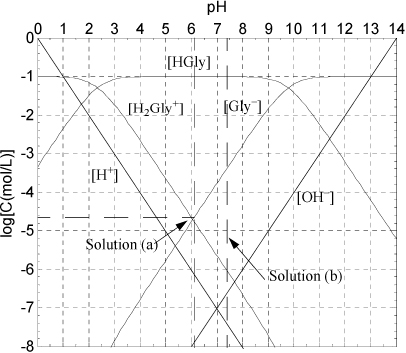
Figure 18.9. Sillèn diagram for 0.1 M glycine discussed in Example 18.7.
a. The relevant equilibria are given in Eqns. 18.64 and 18.65. The material balance is
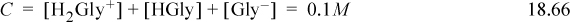
The charge balance is
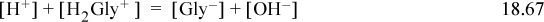
The pH is expected to be near neutral because the glycine added is neither an acid nor a base, though it has both functionalities. Look at the charge balance and the Sillèn plot of concentrations near neutral pH. On the left-hand side of the charge balance, the concentration of [H+] is about an order of magnitude smaller than [H2 Gly+] making the total positive charge concentration about 1.1[H2 Gly+]. On the right side, [Gly–] is over three orders of magnitude larger than [OH–]. Thus, the charge balance is effectively
The answer is found at pH = 6.1. [OH–] = 10–(14–6.1) = 10–7.9 M. The glycine species concentrations are quickly read from the graph, [HGly] = 10–2 M, [Gly–] = 10–4.65 M, [H2 Gly+] = 10–4.75 M. Note the glycine is almost totally in the zwitterion form and the charged forms are about 3.5 orders of magnitude smaller. The final verification of the concentrations is left as a homework problem. Note that if the concentration of glycine was lower, [H+] would become more important in the charge balance.
b. First, [OH–] = 10–(14–7.4) = 10–6.6 M. The glycine species concentrations are quickly read from the graph, [HGly] = 10–2 M, [Gly–] = 10–3.4 M, [H2 Gly+] = 10–6.05 M.
Summary for Use of Sillèn Plots
Throughout this section, we have demonstrated the use of Sillèn plots for weak acids and bases, and polyprotic systems including amino acids. We have demonstrated that the equilibrium relations plotted on the diagram are not directly dependent on the other ions present in the system. The material balance is often combined with the charge balance to yield a proton condition. The proton condition focuses on the intermediate concentrations, by canceling out the overwhelmingly large concentrations, enhancing precision. The proton condition is used along with the plot to determine an approximate solution. In cases where the curves for the dominant species with the same charge sign in the proton condition are close to each other, the curve values are added together and replotted to find the solution graphically (cf. Example 18.6).
For polyprotic systems we have demonstrated that the distribution can easily be calculated by the Sillén method (cf. Example 18.6). For the polyprotic systems in the examples, the pKa values were well separated and each species has a pH where it is the dominant species and the species concentration is virtually equal to the overall concentration, C. For example, in the case of glycine, the intermediate species HGly is virtually equal to C in the range of 4 < pH < 8 (cf. Fig. 18.9). In some polyprotic systems, the pKa.A values are close together—for example, in succinic acid, where the species are H2Succ, HSucc–, and Succ2–. In these cases, the plot maxima in the intermediate species concentration (HSucc– in the case of succinic acid) will not extend all the way up to C. When the diagram is prepared, the regions with sloping lines should be drawn first. Then, if the maxima are not obvious, the full equations for the distribution can be developed as illustrated in Example 18.6 and then plotted for the intermediate species.
18.10. Applications
To introduce the concepts of electrolytes, we started in Section 18.2 with examples of freezing point depression, osmotic pressure, and boiling point elevation. Here we consider other applications where some of the subtler effects of charges are important.
Buffers
When salts and acids that share a common ion are present in solution, the solution is buffered. A buffered solution is resistant to changes in pH, and such behavior is critical in biology. For example, blood is buffered to be at pH 7.4 with carbonates, and slight deviations can cause severe illness. The buffering capacity is dependent on the concentrations of the acid and salt. For a given overall concentration, the buffering capacity is best understood relative to a titration curve. The buffering capacity (for a change in either pH direction) is greatest when the acid is “half” titrated. The fundamental explanation for the buffering phenomenon is because the titration curve is steepest when the acid is half titrated. For a monoprotic acid, this occurs when the acid and salt concentrations are equal, and the buffered pH = pKa,A unless the buffer is very dilute such that the acid/base lines are close to the [H+] or [OH–] lines on a Sillèn diagram. Consider a weak monoprotic acid HA (species A) and the sodium salt NaA, (species B). A specific case would be a mixture of acetic acid and sodium acetate in water. The equations are an extension of Eqns. 18.25–18.28:
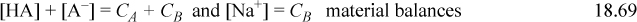
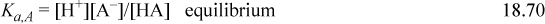
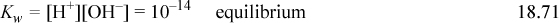
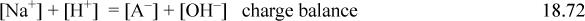
The sodium material balance is inserted into the charge balance, and solving for [A–],
If this is substituted for [A–] in the acid balance,
Substituting into the equilibrium Eqn. 18.70,
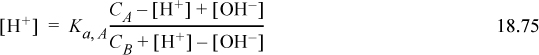
When the [H+] and [OH–] are much smaller than CA and CB the right-hand side simplifies, resulting in the Henderson-Hasselbalch equation:
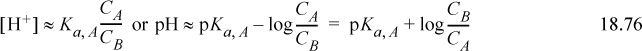
The Sillèn graph method can certainly be used, but the Henderson-Hasselbalch equation is convenient under proper conditions. When CA and CB are near [H+] or [OH–], the equation can lead to absurd results. A better approximation is
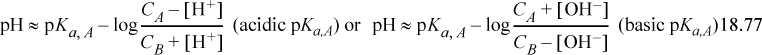
The equations can be used iteratively from an initial assumed value of [H+] or [OH–].
Isoelectric Point and Ionic Strength
Proteins and biomolecules frequently have charged surfaces at neutral pH due to the carboxylic acid and amine side chains. Basic amines are protonated at neutral pH values and acidic carboxylic acids are deprotonated. When the biomolecules have a net charge, they repel each other, and are thus more soluble, enabling them to provide important biological functions by remaining soluble. Two important phenomena exhibited by charged molecules are the change in solubility as the pH is changed, and the dependence of solubility on ionic strength (salt concentration).
First of all, as the pH is varied, the charges on the side chains change. The pH value at which the biomolecule has no net charge is called the isoelectric point. Solubility is usually smallest at the isoelectric point because the lack of net charges permits the large macromolecules to approach each other and the large cooperative physical forces cause them to precipitate. Therefore, solubility typically increases rapidly on either side of the isoelectric point. The isoelectric point is often characterized by the pI which is the isoelectric point pH. Solubility of a milk protein β-lactoglobulin is shown in Fig. 18.10.
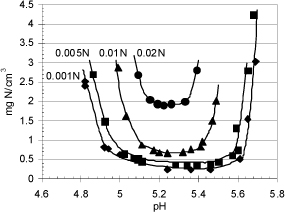
Figure 18.10. Salting in and illustration of minimum solubility at the isoelectric point for milk protein β-lactoglobulin as a function of pH and ionic strength. Gronwall, A., 1942. C.R. Trav. Lab. Carlsberg, Ser. Chim. 24:185-200.
The solubility of biomolecules increases at low ionic strength when the ionic strength (ion concentration) increases. This effect is called salting in and occurs because the ions in solution screen the surface charges. This reduces attractions between positive and negative charges, even near the isoelectric point. There are usually positive and negative charges when the net charge is zero, (cf. amino acid and zwitterion section above) which lead to net attraction. However, at high ionic strength (high salt concentrations), the opposite effect is seen and increasing salt concentrations result in decreasing biomolecule solubility, known as salting out. Salting out occurs because the ionic strength is so high that it screens the repulsive forces that would normally prevent precipitation. Thus, the solubility increases with salt concentration at low salt loading, but decreases with salt concentration at high salt loading, causing a maximum in solubility at intermediate salt concentrations. Observe in Fig. 18.10 the salting in behavior and the minimum solubility near the isoelectric point at all ionic strengths.
Donnan Equilibria
Membranes can have interesting effects when they are impermeable to certain ions or charged species. DNA is a polyanion and requires cations to balance its negative charge. For example, consider a membrane impermeable to DNA shown in Fig. 18.11 where an arbitrary DNA of charge –z is shown in the presence of KCl. The chemical potential of the apparent KCl must be the same on both sides of the membrane, resulting in
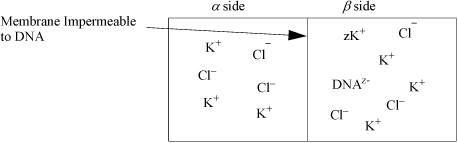
Figure 18.11. Illustration of Donnan Equilibria for DNA. DNA cannot cross the membrane. A larger concentration of ions will exist on the β side, creating higher pressure on the β side due to osmotic pressure.
Electroneutrality requires
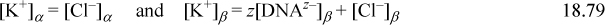
Using concentrations to approximate activities and combining the charge and equilibrium relations results in
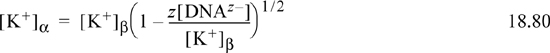
It is clear that the concentration of potassium on the β side is larger due to the minus sign in the parentheses. Similarly, manipulation for chlorine shows that the concentration on the α side is larger, due to the plus sign in the parentheses:
What is the relative magnitude of the terms in parentheses in Eqns. 18.80 and 18.81? Substitute Eqns. 18.80 and 18.81 into the left side of Eqn. 18.78, and it becomes obvious that the product of the two terms in parentheses is 1. What may not be immediately clear is that mathematically there are more dissolved species on the β side, creating a higher osmotic pressure on the β side. Hemoglobin in red blood cells contributes to a Donnan effect because it is confined to the cells. Another interesting effect is that counter anions such as chloride, bicarbonate, and hydroxyl can pass through the membrane and impact the pH of blood because they are bases.
Solubility and Ksp
Dissociation of species can have a dramatic effect on solubility in water. Consider the behavior of fluconazole in Example 18.4. How might the dissociation affect the solubility? Since the solubility is dependent on the activity of the un-ionized species, the solubility goes up appreciably as the equilibrium shifts to the protonated form below the pKa,A.
Example 18.8. Dissociation and solubility of fluconazole
In Example 18.4 the dissociation of fluconazole (fluc) was considered. The solubility can be modeled using (on the molality scale)
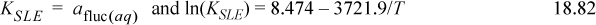
Determine the solubility of fluconazole at pH 7 and pH 1.5 and the distribution of species in solution at 298.15K. Assume ideal solutions.
Solution
This involves two simultaneous equilibria, dissociation and solubility. Note that the acid form of the reaction equilibrium constant is
Ka,A = [fluc][H+]/([fluc+]aH2O)
Since the pH is specified, the solution is so dilute (thus aH2O = 1), and the Ka,A is constant, the ratio [fluc]/[fluc+] is constant at a given pH. From the earlier example, at pH 7, the reciprocal is [fluc+]/[fluc] = 0, and at pH 1.5, [fluc+]/[fluc] = 9.9/5.1 = 1.94.
At 298.15 K, KSLE = 0.018. Using the ideal solution approximation, [fluc] = 0.018 m. This is independent of pH. At pH 7, virtually no [fluc+] is present and thus the solubility is 0.018 mol/L, or using the molecular weight, 0.018 mol/L(306.27 g/mol) = 5.5 g/L.
At pH 1.5, the [fluc] = 0.018 m and [fluc+] = 1.94[fluc], thus the total solubility is 2.94(0.018) = 0.0529 mol/L, or 0.0529(306.27) = 16.2 g/L. The pH makes a large difference in the solubility!
Common Ion Effect
When compounds in solution share a common ion and one of the compounds is near or at the solubility limit, addition of the other species can induce precipitation of the first. For example, consider a solution of water saturated with KCl. If a small amount of NaCl is added to the solution, additional KCl precipitates because the equilibrium is disrupted.
Because the activity of Cl is increased when NaCl is added, the activity of K must be decreased to match Ksp, thus additional KCl precipitates. Likewise, KCl affects the solubility of NaCl near its solubility limit.
18.11. Redox Reactions
Chemical reactions involving electron transfers are fundamental steps in diverse applications ranging from biological systems to corrosion, batteries, and fuel cells. Electron losses are called oxidations and reactions involving gains in electrons are called reductions. A simple acronym to remember the conventions is OILRIG; oxidation is loss, reduction is gain. To balance electrons, an oxidation reaction is always coupled with a reduction reaction, and the combined reactions are termed redox reactions.
Redox reactions can be conducted in any phase. Even combustion of methane is a redox reaction where carbon is oxidized into CO2 and O2 is reduced into water. Though “oxidation” sounds like it is limited to reaction with oxygen, the process is much more general, relating to the loss of electrons. The gas phase combustion of methane does not produce useful electrons. However, biological oxidation carries out the oxidation of glucose in a series of smaller steps, capturing the electrons and by coupling the favorable oxidation to otherwise unfavorable reactions. In a battery, the redox reaction is enabled by electron flow through an external circuit and a voltage is generated. By permitting the spontaneous redox reaction through an external circuit, we obtain electrical power.
Li-ion batteries power the majority of portable devices today. They are constructed of electrodes of CoO2 and graphite (represented here as C6 to stress the aromatic ring structure and the way each ring can host one cation). Li+ and e– are shuttled back and forth during discharge and charge. During battery discharge, an oxidation of graphite is occurring at the anode, LiC6 C6 + Li+ + e– (remember that oxidation is loss, so electrons are generated at the anode), and reduction of Co from Co+4 to Co+3 at the cathode, CoO2 + Li+ + e– LiCoO2. The overall discharge reaction is LiC6 + CoO2 C6 + LiCoO2. The electrons are carried through the external circuit while the Li+ are not capable of flowing through the circuit, but travel through an electrolyte solution between the electrodes in the opposite direction as the electrons. The combination of the electrodes and electrolyte is called an electrochemical cell or battery. The Li-ion cell produces about 3.9V. To charge the cell, an opposing voltage > 3.9V must be applied. The life of the cell depends upon chemical reversibility, side reactions, and physical changes that may affect transport or the ability of the Li+ to be hosted by the graphite sheets or the CoO2.
Half-Reactions
Redox reactions can be decoupled into the corresponding reduction and oxidation processes as we have indicated with the battery example above. For example, look at the overall reaction for the battery above and note that the reaction does not show the electrons! From the overall battery reaction, how do we determine the two half-reactions, how many electrons are transferred, the voltage, and the direction of electron flow?
As with other thermodynamic tables a reference is used to establish a relative scale. Because reduction reactions are always coupled to oxidation reactions, measurement of absolute potentials is not possible. The reference for redox reactions is to measure/tabulate reduction reactions relative to a standard H2 electrode. In the standard H2 electrode, an acid solution is used to establish aH+ = 1 (pH = 0) at 298.15K and H2(g) is bubbled through the solution at 1 bar partial pressure;15 the reaction 2H+ + 2e– H2(g) is conducted on a submersed platinum electrode. This reaction is a reduction of H+. The direction of the reaction depends on whether the reduction potential for the other electrode is greater than or less than that of hydrogen. The potential for hydrogen ion reduction is arbitrarily set to zero at the standard conditions cited above, permitting determination of other reduction potentials. The convention established by the International Union of Pure and Applied Chemistry, (IUPAC) is to always tabulate the potential for reduction reactions.16 The oxidation potential is the negative of the reduction potential. Standard reduction potentials determined at 298.15 K and molal activity of unity (usually near 1 m) for a variety of reactions are tabulated in Appendix E.17 The half-reaction with the higher reduction potential undergoes reduction at standard conditions in the electrochemical reaction, regardless of the number of electrons in the half-reaction. The other reaction proceeds in the direction of oxidation at standard conditions. The relation between the overall cell voltage and the Gibbs energy of reaction at equilibrium is
Michael Faraday (1791–1867) established the concept of an electromagnetic field, and also popularized the terms “anode,” “cathode,” “electrode,” “ion.”
where ne is the number of electrons transferred in the balanced pair of redox reactions, F is Faraday’s constant 96,485 J/V, and E° = E°red – E°ox is the difference in reduction potentials of both half-reactions (or you may wish to think of adding the reduction potential and the oxidation potential). Note that the potential is measured per electron, and thus the potentials can be combined without balancing. However, the number of balanced electrons is necessary to relate the potential to the equilibrium constant, Gibbs energy, or nonstandard conditions. As discussed in Section 18.6, Gibbs energies for steps are additive for an overall reaction; the principle can be applied to the half-reactions, ΔG° = – neFE°red + neFE°ox, where E°red and E°ox both represent reduction potentials. A redox reaction at equilibrium is not useful because there are no driving forces. Instead, the direction of the reaction at nonstandard conditions is dependent on ΔG. The principles of Chapter 17 also apply, even under nonstandard conditions, and the reaction goes forward for ΔG < 0, and backward for ΔG > 0. We write
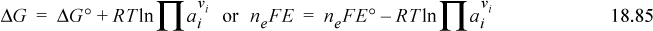
This is often presented as the Nernst equation. Also, since reactions frequently occur near 298.15 K, and log is more convenient than ln for quick calculations, the equation is frequently written with values inserted,
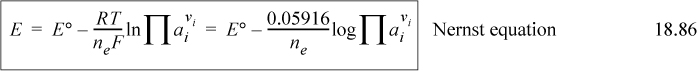
Walther Nernst (1864–1941) is credited with development of the third law of thermodynamics, for which he was awarded the 1920 Nobel Prize in chemistry.
where the last equation is limited to 298.15 K. The voltage of a cell is determined by E, not directly by E°.
Balancing Redox Reactions
Suppose that you want to design a battery and evaluate the voltage that would be generated. The conventional presentation of thermochemical information is organized in tables of half-cell reactions. After determining the two half-cell reactions and finding them in tables, the two half-cell reactions are balanced and then combined to determine the overall cell voltage. The steps to identify the half-reactions and reaction direction are: 1) identify the oxidized and reduced species using oxidation states (the procedure to determine oxidation states is summarized in Table 18.3)18; 2) break the reactions into two half-reactions; 3) for each half-reaction, balance the number of atoms for the species oxidized or reduced; 4) balance the change in oxidation state by adding the correct number of electrons to one side of each half-reaction; 5) balance oxygen by adding H2O to one side of each half-reaction; 6) balance the hydrogen by adding H+ to the appropriate side (the total charge on both sides of the reactions should now be the same.); 7) look up the reduction potential for each reaction and write the reaction with the smaller reduction potential as the oxidation reaction; 8) multiply the reactions by the smallest integers such that when they are added the electrons cancel; and 9) determine the Gibbs energy and equilibrium condition from Eqn. 18.85 or 18.86 for nonstandard conditions. Note that if the reaction is under basic conditions, it may be more appropriate to work with the basic form. Because OH– and H2O both involve H and O, it is easiest to balance with H+ and then use the water dissociation reaction to convert the reaction as shown in Example 18.9.
Table 18.3. Procedure to Determine Oxidation States
Steps to determine standard cell potential and direction of reaction.
Including Nonredox Reactions
Frequently, it is necessary to combine redox reactions with reactions that do not involve oxidation and reduction, such as a dissociation or solubility, or use the dissociation reaction of water to convert the acid form (reactions using H+) to a basic form (reactions using OH–). This is rigorously done using the Gibbs energy of formation. To combine the reactions: (1) write all the individual reactions balanced so that they add to give the overall balanced reaction as explained above and include the desired nonredox reaction; (2) determine the Gibbs energies for the constituent balanced reactions; (3) add the reactions and Gibbs energies together and then divide the overall Gibbs energy by F and ne using the Nernst equation to find E°. The concepts for combining reactions are shown in Example 18.9 where acidic half-cell reactions are transformed to basic reactions.
Example 18.9. Alkaline dry-cell battery
Consumer portable electronics are commonly powered by ‘alkaline’ dry-cell batteries. These cells use an alkaline paste instead of an aqueous solution. The moisture content is low to minimize leakage, and the alkaline solution is used instead of acid because the degradation of the electrodes is slower in alkali compared to acid. The relevant species are Zn(s), ZnO(s), γ-MnO2(s), and α-MnOOH(s). A new battery has Zn(s) and γ-MnO2(s) electrodes.
a. Determine the balanced reactions for H+ and then transform them to use OH–. Then provide the balanced overall reaction. (b) Determine the voltage generated by the cell when [OH–] = 1 m and [OH–] = 1.1 m, and the Gibbs energy of reaction.
Solution
The oxidation states of Zn are 0 for Zn(s) and +2 for ZnO(s); of Mn are +4 for MnO2(s) and +3 for α-MnOOH(s). Since the initial electrode is Zn(s) and γ-MnO2(s), Zn is being oxidized (losing electrons) and Mn is being reduced during battery use.
a. For Mn, the half-cell reduction reaction is found to be γ-MnO2(s) + H+ + e– α-MnOOH(s), through the following procedure. Start with the Mn species (MnO2 and MnOOH) on each side of the reaction (more reduced on the right). The reduction requires one electron to go from +4 to +3, so one electron is added to the left. At this point, the O is already balanced, and one H+ is added to the left to balance hydrogen. The total charge is 0 on each side of the reaction. To convert to the base form, we add H2O H+ + OH–, giving γ-MnO2(s) + H2O + e– α-MnOOH(s) + OH– and the total charge is –1 on each side of the reaction.
For the other electrode, the half-cell reduction reaction is found to be ZnO(s) + 2H+ + 2e– Zn(s) + H2O through the following procedure. After writing the Zn species on each side (more reduced on the right), we note that the reaction requires two electrons and add them to the left, water is added on the right side to balance oxygen, then 2H+ are added to the left side to balance H. The total charge is 0 on each side. To convert to the base form, we add 2H2O 2H+ + 2OH–, giving ZnO(s) + H2O + 2e– Zn(s) + 2OH–.
For the overall reaction, to balance electrons, two Mn must be reduced for each Zn oxidized. Combining, Zn(s) + 2γ-MnO2(s) + H2O ZnO(s) + 2α-MnOOH(s).
b. The voltage is found by taking the difference in reduction potentials found in Appendix E. The standard potential is found by the differences in reduction potentials, E° = 0.3 – (–1.26) = 1.56 V. The potential under operating conditions is given by
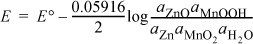
Since all the species except for H2O are solids, they exist in the pure state as a first approximation. (In actual practice the MnOOH forms a solid solution with MnO2, but we ignore the effect here.) The activity of water is near 1 in the paste and [OH–] does not appear, and thus it has no effect on the equilibrium voltage. Therefore, the battery should give a constant 1.56 V throughout its life.
Note that we are neglecting transport effects and the solid solution behavior. Thus, the actual voltage drops as the battery dies owing in part to these effects. The Gibbs energy of reaction is ΔG = –neFE = –2(96485)1.56 = –301 kJ/mol, a spontaneous reaction when the circuit is closed.
Fuel Cells
Fuel cells offer many potential advantages for energy usage. They are similar to a battery in that they involve oxidation at the anode and reduction at the cathode. Like the battery discussed above, they also involve transport of molecular cations between the electrodes. The primary difference is that the oxidizing and reducing species are considered to be “fuels” that either flow past the electrodes, or are fuels that can be replenished.
Fuel cell technology is in a state of rapid change. Typical issues revolve around the economical choice of fuels and the longevity of fuel cell devices. Nevertheless, the promise of converting chemical energy into electrical energy without the limitations of the Carnot cycle is a significant motivation. A biological fuel cell is considered in Example 18.11. The status of this topic is addressed in an online supplement with particular emphasis on the thermodynamic aspects of this technology.
Leave a Reply