The thermodynamic quantities internal energy, entropy, enthalpy, Helmholtz energy, Gibbs energy, and chemical potential provide the framework for the solution of both types of problems previously described. Although the absolute values of the thermodynamic quantities cannot be determined, changes in these properties can be computed accurately. However, these computations require the knowledge of the volumetric behavior of the substance; that is, the quantitative relationship between the pressure, volume and temperature for the substance. Figure 8.5 shows a typical representation of the volumetric behavior of a pure substance on a P-V diagram [4]. The solid lines are isotherms, representing the relationship between the pressure and volume at a constant temperature.
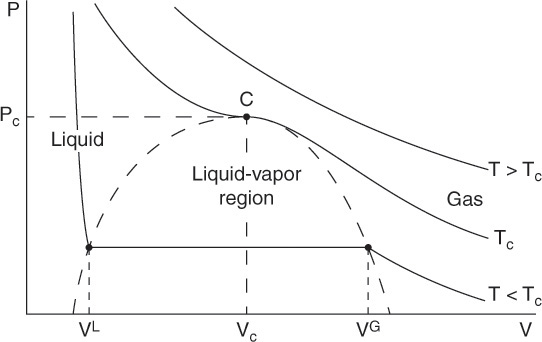
Figure 8.5 Pressure-volume phase diagram for a pure substance.
Source: Kyle, B. G., Chemical and Process Thermodynamics, Third Edition, Prentice Hall, Upper Saddle River, New Jersey, 1999.
Point C in the figure represents the critical point, with coordinates of VC (critical volume) and PC (critical pressure). The isotherm at the critical temperature TC is tangent to the curve represented by the dashed line. This curve represents a boundary between the two-phase vapor-liquid region and the single-phase region. Isotherms at supercritical temperatures (T > TC) lie entirely within the gas phase region. The volumetric behavior is more complicated at subcritical temperatures, where depending on the pressure, both liquid and vapor coexist.
The volumetric behavior of a pure substance can also be represented on a pressure-temperature (P-T) diagram, as shown in Figure 8.6 [5]. Point F represents the triple point for the substance where all three phases—solid, liquid, and vapor—coexist. The solid lines from F represent the boundaries between different phases, F-S represents the boundary between solid and liquid, and F-C represents the boundary between liquid and vapor. C, as in Figure 8.5, is the critical point, and the supercritical region has pressure and temperature greater than PC and TC, as shown. The dashed lines are isochores, that is, lines of constant volume.
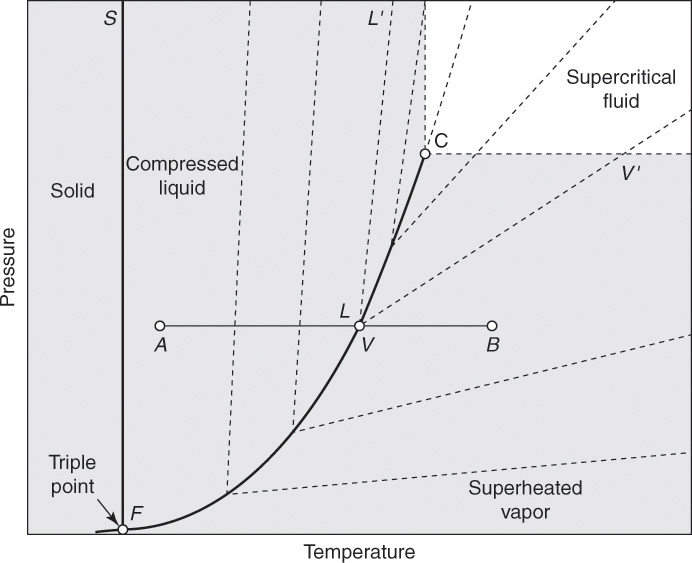
Figure 8.6 Pressure-temperature phase diagram for a pure substance.
Source: Matsoukas, T., Fundamentals of Chemical Engineering Thermodynamics with Applications to Chemical Processes, Prentice Hall, Upper Saddle River, New Jersey, 2013.
The simplest of the P-V-T relationships is described by the ideal gas law:

Here, n is the number of moles of the gas, and R is the universal gas constant.
The expression for the ideal gas law can be obtained by combining empirical Boyle’s6 and Charles or Gay-Lussac7 laws, or it can be derived from the kinetic theory of ideal gases [9]. Two of the fundamental postulates of the kinetic theory involve the assumptions of no intermolecular forces and negligible volume of molecules. However, molecules of real substances do occupy certain volume, small though it may be. Further, these molecules do exert different types of attractive and repulsive forces on each other, with the result that the behavior of real substances cannot be accurately described by the ideal gas law. It follows that this lack of accuracy would lead to errors in the computation of thermodynamic properties. An accurate mathematical description of the volumetric behavior of substances—the equation of state (EOS)—is a fundamental need for any thermodynamic calculations.
6. Gas volume is inversely proportional to its pressure.
7. Gas volume is directly proportional to its absolute temperature.
Several different types of EOSs have been reported in literature [5]. Some of the equations are empirical, some are semi-empirical, and many others are developed from first principles. One of the earliest equations describing the behavior of real gases is the van der Waals equation, written in its pressure-explicit form [5]:

In this equation, v is the molar volume of the gas (=V/n), and a and b are the characteristic constants for the gas. The constant a is related to the attractive force between the molecules, and b is the effective physical volume occupied by a mole of the gas. These two constants are typically calculated from two other characteristic constants unique to each substance: the critical pressure Pc and critical temperature Tc. The critical constants for a large number of substances are available from the sources mentioned in Chapter 7.
The van der Waals equation belongs to a class of EOSs called the cubic equations of state, as they form a third-order polynomial in v. Several other types of EOSs are available that may describe the volumetric behavior of some classes of compounds accurately but fail for others. A chemical engineer must select the appropriate EOS for the system under consideration and perform computations using that equation.
Leave a Reply