We end the chapter by providing examples of unsteady-state open systems. The first example shows that analysis of such systems can produce results quite consistent with expansion in a piston/cylinder.
Example 4.19. Entropy change in a leaky tank
Consider air (an ideal gas) leaking from a tank. How does the entropy of the gas in the tank change? Use this perspective to develop a relation between Tf and Pf and compare it to the expression we obtained previously by the energy balance.
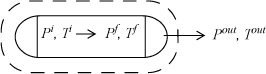
Solution
m-Balance: dn = – dnout
S-Balance: 
But physically, we know that the leaking fluid is at the same state as the fluid in the tank; therefore, the S-balance becomes 
, or ΔS = 0.
For an ideal gas with a constant heat capacity:
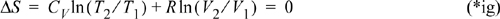
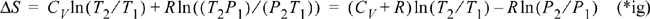
Compare with Example 2.15 on page 81. The entropy balance and energy balance in this case are not independent. Either can be used to derive the same result. This also shows that our analysis in Example 2.15 was assumed to be reversible.
Illustration that the energy and entropy balances may not be independent.
The next example builds on the first by adding a turbine to the tank. Note the method by which the system is subdivided to solve the problem.
Example 4.20. An ideal gas leaking through a turbine (unsteady state)
A portable power supply consists of a 28-liter bottle of compressed helium, charged to 13.8 MPa at 300 K, connected to a small turbine. During operation, the helium drives the turbine continuously until the pressure in the bottle drops to 0.69 MPa. The turbine exhausts at 0.1 MPa. Neglecting heat transfer, calculate the maximum possible work from the turbine. Assume helium to be an ideal gas with CP = 20.9 J/mol-K.
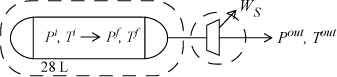
Consider a balance on the tank only. The result of the balance will match the result of Example 4.19.
Writing an entropy balance for a reversible adiabatic turbine only,
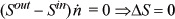
which shows that the turbine also does not change the molar entropy. Thus, the molar entropy of the exiting fluid is the same as the entropy in the tank, which is identical to the molar entropy at the start of the process. Therefore, the molar entropy and the pressure of the exiting gas are fixed. Since only two intensive properties fix all other intensive properties for a pure fluid, the exiting temperature is also fixed. The relation for an ideal gas along a reversible adiabat gives:
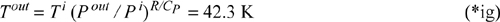
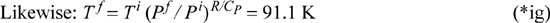
Solution by overall energy balance:
d(nU) = Hout dn + dWS and Hout is fixed since Tout, Pout are fixed; therefore, we may apply hint 4(a) from Section 2.14.
Integrating this expression:
nfUf – niUi = Hout(nf – ni) + WS
Rearranging:
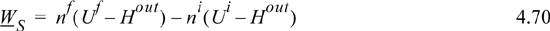
Determining variables in the equation:
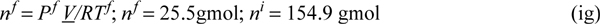
Choose reference temperature, TR ≡ 300 K, ⇒ setting UR = 0, then since HR = UR + (PV)R, and since the fluid is an ideal gas, CV = CP – R = 20.9 – 8.314 = 12.586 J/mol-K:
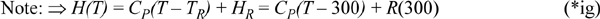
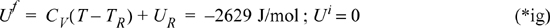
Now, plugging into Eqn. 4.70:
WS = 25.5(–2629 + 2892) – 154.9(0 + 2892)
⇒ WS = –441,200 J
Leave a Reply