Turbine, Compressor, and Pump Efficiency

Our analysis of the Carnot devices supports statement 2 at the beginning of Section 4.3. We have seen that work is maximized/minimized when the entropy generation is zero. Analysis of other processes would verify this useful conclusion. Work is lost by processes which generate entropy. If a device is not internally reversible, work will be lost within the device. Also, even if the device is internally reversible, work may be lost by irreversible interactions with the surroundings. Therefore, in setting up and solving problems to find maximum/minimum work, the objectives must be clear as to whether the system is internally reversible or whether the entire process is reversible. When we apply the entropy balance to a reversible process, the term representing entropy generation is zero.

In Chapter 2, both velocity gradients and friction were discussed as phenomena that lead to irreversibilities. Indeed, entropy is generated by both of these phenomena as well as by heat conduction along temperature gradients discussed in this chapter. Considering factors which affect reversibility (generation of entropy), you may have challenged yourself to consider a practical way to transfer heat with only infinitesimal temperature differences, or move fluid with only infinitesimal velocity gradients. You are probably convinced that such a process would not be practical. Indeed, the rate at which heat is transferred increases as the temperature driving forces increase, and we need finite temperature differences to transfer heat practically. Likewise, a pump will have large velocity gradients. Although we can measure changes in other properties by which we can calculate entropy changes arising from irreversibilities, an a priori prediction of lost work (W_lost) or entropy generated (S_gen) is extremely difficult and generally impractical. Direct evaluation of lost work in process equipment, such as turbines and compressors, is far beyond routine calculation and determined by empirical experience. It may seem that all of the effort to characterize reversible processes will be difficult to relate to real processes.

However, we can use practical experience to relate real processes to the idealized reversible processes. Therefore, in analyzing or designing processes involving operations of this nature, it is often necessary to approximate the real situation with a reversible one in which (W_lost) = 0 (no entropy generation). Past experience with many devices, such as compressors and turbines, often permits the engineer to relate performance under hypothetical reversible conditions to actual operation under real conditions. The relation is usually expressed by means of an efficiency factor. Equipment manufacturers typically provide performance curves as a function of process conditions. For introductory purposes, in this text we use a fixed factor. For devices such as pumps and compressors which utilize work from the surroundings, efficiency is defined as

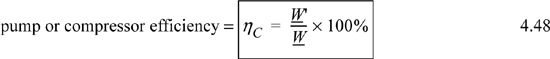
 Primes are used to denote reversible processes.

where the ′ denotes the reversible work. This notation will be used throughout the text when irreversible and reversible calculations are performed in the same problem. For turbines and other expansion devices that supply work to the surroundings, the definition is inverted to give

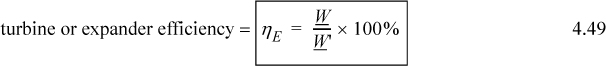
For adiabatic pumps, compressors, turbines, or expanders, the work terms may be calculated from the reversible and irreversible enthalpy changes by application of the energy balance.

Note: The strategy is to first calculate the work involved in a reversible process, then apply an efficiency which is empirically derived from previous experience with similar equipment. The outlet pressure of an irreversible adiabatic turbine or pump is always at the same pressure as a reversible device, but the enthalpy is always higher for the same inlet state. This means that if the outlet of the reversible adiabatic device is a single phase, the outlet of the irreversible adiabatic device will be at a higher temperature. If the outlet of the reversible adiabatic device is a two-phase mixture, the quality for the irreversible adiabatic device will be higher or the outlet could potentially be a single phase.