At low reduced pressure, deviations from ideal gas behavior are sufficiently small that we can write our equation of state as explicit in a power series with respect to density. That is,
where B, C, and D are the second, third, and fourth virial coefficients. This can be considered an expansion in powers of ρ. Coefficients C and D are rarely applied because this power series is not very accurate over a broad range of conditions. The most common engineering application of the virial equation of state is to truncate it after the second virial coefficient and to limit the range of application appropriately. It provides a simple equation which still has a reasonable number of viable applications. It has become common usage to refer to the equation truncated after the second virial coefficient as the virial equation, even though we know that it is really a specialized form. We, too, will follow this common usage. Furthermore, the truncated form may alternatively be expressed as Z = Z(P,T). Hence, we often refer to the virial equation as:
where B is a function of T. Note that Eqn. 7.5 indicates that Z varies linearly with pressure along an isotherm. Look back at Fig. 7.4 and notice that the region in which linear behavior occurs is limited, but in general, the approximation can be used at higher reduced pressures when the reduced temperature is higher. The virial equation can be generalized in reduced coordinates as given by Eqns. 7.6–7.9.5 Eqn. 7.10 checks for restriction of the calculation to the linear Z region.
Virial equation. B is known as the second virial coefficient, and it is a measure of the slope of the Z-chart isotherms in the linear region.
The temperature dependence of the slope of the Z lines is not sufficiently represented by 1/T, so the temperature dependence of B in Eqns. 7.8 and 7.9 is required. The virial equation is limited in its range of applicability, but it has the advantage of simplicity. Its simplicity is especially advantageous when illustrating derivations of real-fluid behavior for the first time and extending thermodynamic relations to vapor mixtures. Unfortunately, the virial equation does not apply to liquids, and many interesting results in thermodynamics appear in the study of liquids. To develop a global perspective applicable to gases and liquids, we must consider the physics of fluids in a more sophisticated manner. The simplest form which still permits this level of sophistication is the cubic equation, discussed in the following section.
Example 7.2. Application of the virial equation
Estimate the specific volume in cm3/g for carbon dioxide at 310 K and (a) 8 bar (b) 75 bar by the virial equation and compare to the experimental values of 70.58 and 3.90, respectively.
Solution
ω = 0.228 and Tr = 310/304.2 = 1.02 for both cases (a) and (b), so,
B0 = 0.083 – 0.422/1.021.6 = –0.326
B1 = 0.139 – 0.172/1.024.2 = –0.0193
B(T)Pc/RTc = B0 + ωB1) = (–0.326 + 0.228·(–0.0193)) = –0.3304
a. Pr = 8/73.82 = 0.108; so Z = 1 + (B0 + ωB1)Pr/Tr = 1 – 0.3304·0.108/1.02 = 0.965 V = ZRT/(P·MW) = (0.965·83.14·310)/(8·44) = 70.66, within 0.1% of the experimental value.
b. Pr = 75/73.82 = 1.016; applying Eqn. 7.10, 0.686 + 0.439·1.016 = 1.13 > Tr = 1.02. Therefore, the virial equation may be inaccurate using only the second virial coefficient.
There is an adaptation of the form of the virial series which should be mentioned before concluding this discussion. It should not seem surprising that the inclusion of extra adjustable parameters in the form of the virial series is an extremely straightforward task—just add higher order terms to the series. In many cases, exponential terms are also included as in Eqn. 7.11. In this way, it is possible to fit the P-V-T behavior of the liquid as well as the vapor to a reasonable degree of accuracy. It turns out that the theoretical foundation for the series expansion in this way is tenuous, however. Reading “the fine print” in discussions of series expansions like the Taylor series shows that such an approach is only applicable to “analytic” functions. At present, there is a general acceptance that the behavior of real fluids is “non-analytic” at the critical point. This means that application of such a series expansion above the critical density and below the critical temperature is without a rigorous mathematical basis. Nevertheless, engineers occasionally invoke the motto that “we can fit the shape of an elephant with enough adjustable parameters.” It is in this spirit that empirical equations like the Benedict-Webb-Rubin equation are best appreciated. One particular modification of the Benedict-Webb-Rubin form is given below. It is the form that Lee and Kesler6 developed to render the Pitzer correlation in terms of computer-friendly equations. The Lee-Kesler equation was used to generate Fig. 7.4.
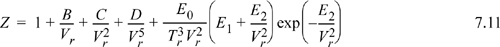
Twelve parameters are used to specify the temperature dependence of B, C, D, E0, E1, and E2 for each compound. Readers are directed to the original article for the exact values of the parameters as part of the homework.
Leave a Reply