In this section, we refer to a division of the universe into the same three subsystems described in Section 2.14 on page 74.
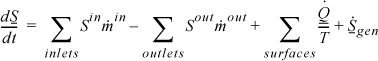
1. T is the system temperature at the location where Q is transferred.
2. Sin, Sout are state variables, and any pathway may be used to calculate the change from inlet to outlet. The pathway for calculation does not need to be the pathway for the actual process.
3. ![]() represents entropy generation due to irreversibilities within the system, e.g., internal heat transfer or conduction, viscous dissipation or mixing of streams of differing composition, or degradation of mechanical energy to thermal energy. Entropy generation at system boundaries is not included in the balance.
represents entropy generation due to irreversibilities within the system, e.g., internal heat transfer or conduction, viscous dissipation or mixing of streams of differing composition, or degradation of mechanical energy to thermal energy. Entropy generation at system boundaries is not included in the balance.
4. Entropy generation may occur at container walls. The entropy generation of the universe must be calculated by summing ![]() for all three subsystems, not just system 1 and system 3.
for all three subsystems, not just system 1 and system 3.
Test Yourself
1. What are the constraints on the sign of ![]() ?
?
2. Consider two isothermal processes both rejecting heat at the same temperature. One process is reversible and the other is irreversible. Which has a larger absolute value of heat transfer?
4.16. Summary
We began the chapter introducing microscopic methods to calculate entropy. We demonstrated that entropy increases when volume (for a gas) or temperature increases. Thermal energy is really a means of representing the randomness due to accessible microstates, such that the concept is best understood in terms of the microscopic definition of entropy. We showed that the macroscopic definition was consistent with the microscopic definition. We showed that entropy is essential for analysis of reversibility for processes, because irreversible processes generate entropy. We demonstrated that reversible Carnot cycle thermal efficiency was easily evaluated using entropy. The primary impact for pure-fluid applications is that compressors and turbines can be analyzed using empirical efficiencies relative to reversible devices. On a broader scale, however, you should appreciate the limitations of the conversion of heat into work.
This chapter is relatively long because mastering computations involving entropy can be challenging. Students may be familiar with energy balances and heats of reaction from previous courses, but entropy may seem new and abstract. Therefore, many examples have been provided. Students are encouraged to review these and the practice problems at the end of the chapter. The best way to develop a comfort level with entropy is to practice and learn by doing.
Important Equations
Entropy is a state change, and for an ideal gas,
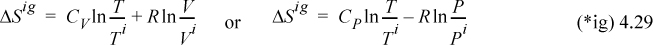
For a condensed phase, the first term of the second equation should be used for a first approximation using the heat capacity for the appropriate phase.
Of course, the most important equation of this chapter is the complete entropy balance, but it may be convenient to remember some of its most common simplifications.
ΔS = 0 for a fluid in an adiabatic reversible process, like across a steady-state adiabatic reversible compressor or turbine or within an unsteady-state adiabatic reversible piston/cylinder.
ΔS = Qrev/T for a fluid in any process, like an isothermal reversible compressor. For an irreversible process, we design a reversible pathway to the actual final state.
ΔS = 0 for a the entropy in a reversible adiabatic leaking tank.
Pay careful attention to the subtle distinctions between these equations. A common mistake is to write ΔS = 0 whenever you see the word “reversible.” Remember that reversibility is coupled to entropy generation, not directly to S or ΔS. For entropy changes of a fluid, a smart approach is to write ΔS = Qrev/T always and then scratch a line through Qrev after you deliberately determine that the process is adiabatic and reversible. A fluid in an irreversible adiabatic process will have an entropy change (and Qrev) even though the actual heat transfer is zero. Note that the entropy balance uses the actual heat transfer, Q, not Qrev. Only for a reversible process are they identical.
The distinction between ΔS = 0 and ΔS = 0 is perhaps subtler. By writing ΔS = 0, we emphasize that only the specific entropy of the fluid remains constant. When ΔS = 0 for an open system, the quantity ΔS = nfSf – niSi = SΔn will be non-zero whenever S is not at the reference state.
Disorder must increase if two different gases are mixed slowly and adiabatically, but it is difficult to see how to compute the entropy change from the macroscopic definition of dS. For ideal solutions, the relation developed from the microscopic approach is:

This equation is useful for estimating the effects of mixing in many situations, even beyond the assumption of ideal gases from which it derives. Eqn. 4.8 also conveys how disorder and mixing are not strictly related to heating, as one might infer from the macroscopic definition of entropy. The entropy of mixing will be of major importance in Unit III in the discussion of mixtures.
4.17. Practice Problems
P4.1. Call placement of a particle in box A, “heads” and placement in box B, “tails.” Given one particle, there are two ways of arranging it, H or T. For two particles, there are four ways of arranging them, {HH,HT,TH,TT}. We can treat the microstates by considering each particle in order. For example, {H T H H} means the first particle is in box A, the second in box B, the third in box A, and the fourth in box A.
a. List and count the ways of arranging three particles. Now consider four particles. What is the general formula for the number of arrangements versus the number of particles? (ANS. 2N)
b. How many arrangements correspond to having two particles in box A and one in box B? What is the probability of {2H,1T}? (ANS. 3/8)
c. How many arrangements correspond to {2H,2T}. {3H,2T}. {4H,2T}. {3H,3T}? (ANS. N!/[(N – m)!m!])
d. List the macrostates and corresponding number of microstates for an eight-particle, two-box system. What portion of all microstates are parts of either 5:3, 4:4, or 3:5 macrostates? (ANS. 71%)
e. What is the change of entropy in going from a 5:3 macrostate to a 4:4 macrostate? (ANS. 3.08E-24 J/K)
f. Use Stirling’s approximation to estimate the change of entropy in going from a distribution of 50.1% of 6.022E23 in box A to a distribution of 50.001%, and from 50.001% to 50.000%. (ANS. 1.2E18 J/K)
P4.2. Twenty molecules are contained in a piston + cylinder at low pressure. The piston moves such that the volume is expanded by a factor of 4 with no work produced of any kind. Compute ΔS/k. (ANS. 23.19)
P4.3. Fifteen molecules are distributed as 9:4:2 between equal-sized boxes A:B:C, respectively. The partitions between the boxes are removed, and the molecules distribute themselves evenly between the boxes. Compute ΔS/k. (ANS. 11.23)
P4.4. Rolling two die (six-sided cubes with numbers between 1 and 6 on each side) is like putting two particles in six boxes. Compute ΔS/k for going from double sixes to a four and three. (ANS. 0.693)
P4.5. Estimate the change in entropy when one mole of nitrogen is compressed by a piston in a cylinder from 300 K and 23 liters/mol to 400 K and 460 liters/mol. (CP = 7/2R) (ANS. 1.07 kJ/kgK)
P4.6. Steam at 400°C and 10 bar is left in an insulated 10 m3 cylinder. The cylinder has a small leak, however. Compute the conditions of the steam after the pressure has dropped to 1 bar. What is the change in the specific entropy of the steam in the cylinder? Is this a reversible process? The mass of the cylinder is 600 kg, and its heat capacity is 0.1 cal/g-K. Solve the problem with and without considering the heat capacity of the cylinder. (ANS. (a)~120°C; (b) 360°C)
P4.7. A mixture of 1CO:2H2 is adiabatically and continuously compressed from 5 atm and 100°F to 100 atm and 1100°F. Hint: For this mixture, CP = x1CP1 + x2CP2.
a. Estimate the work of compressing 1 ton/h of the gas. (CP = 7/2R) (ANS. 1.3E6 BTU/h)
b. Determine the efficiency of the compressor. (ANS. 76%)
P4.8. An adiabatic compressor is used to continuously compress nitrogen (CP/R = 7/2) from 2 bar and 300 K to 15 bar. The compressed nitrogen is found to have an outlet temperature of 625 K. How much work is required (kJ/kg)? What is the efficiency of the compressor? (ANS. 9.46 kJ/mol, 72%)
P4.9. An adiabatic compressor is used to continuously compress low-pressure steam from 0.8 MPa and 200°C to 4.0 MPa and 500°C in a steady-state process. What is the work required per kg of steam through this compressor? Compute the efficiency of the compressor. (ANS. 606 J/g, 67%)
P4.10. An adiabatic turbine is supplied with steam at 2.0 MPa and 600°C and the steam exhausts at 98% quality and 24°C. Compute the work output per kg of steam. Compute the efficiency of the turbine. (ANS. 1.2E3 kJ, 85%)
P4.11. An adiabatic compressor has been designed to continuously compress 1 kg/s of saturated vapor steam from 1 bar to 100 bar and 1100°C. Estimate the power requirement of this compressor in horsepower. Determine the efficiency of the compressor. (ANS. 3000 hp, 60%)
P4.12. Ethylene gas is to be continuously compressed from an initial state of 1 bar and 20°C to a final pressure of 18 bar in an adiabatic compressor. If compression is 70% efficient compared with an isentropic process, what will be the work requirement and what will be the final temperature of the ethylene? Assume the ethylene behaves as an ideal gas with CP = 44 J/mol-K. (ANS. 13.4 kJ/mol, 596 K)
P4.13. Operating a wind tunnel for aircraft experiments begins with adiabatically and reversibly compressing atmospheric air (300 K) into long cylinders comprising a total volume of 20 m3 at 200 bars. The cylinders are initially at 1 bar. Estimate the minimal amount of work required (MJ) to perform the compression step. (ANS. online.)
a. Write the most appropriate energy balance(s) for this process. Clearly identify the system(s) pertaining to your energy balance(s). Explain your reasoning briefly.
b. Write the most appropriate entropy balance(s) for this process. Clearly identify the system(s) pertaining to your entropy balance(s). Explain your reasoning briefly.
c. Solve for the minimal amount of work required (MJ) to perform the compression step.
P4.14. As part of a refrigeration cycle, Freon 134a is adiabatically compressed from the saturated vapor at –60°C (note the negative sign on temperature) to 1017 kPa and 100°C.
a. How much work is required in kJ/kg?
b. Estimate the efficiency of the compressor.
(ANS. 121, 75%)
P4.15. Steam is produced at 30 bar and some unknown temperature. A small amount of steam is bled off and goes through an adiabatic throttling valve to 1 bar. The temperature of the steam exiting the throttling valve is 110°C. What is the value of the specific entropy of the steam before entering the throttle? (ANS. 5.9736 J/g-K)
P4.16. Suppose the expansion in problem P2.19 was completely adiabatic instead of isothermal and CP = 7 cal/(mol-K). How would the height of the piston be affected? Must we generate heat or consume heat to maintain isothermal operation? (ANS. decrease, generate)
P4.17. It is desired to determine the volume of an initially evacuated tank by filling it from an 80 liter cylinder of air at 300 bar and 300 K. The final pressure of both tanks is 5 bars. Estimate the volume in liters. (ANS. 4720 L)
P4.18. An insulated cylinder is fitted with a freely floating piston, and contains 0.5 kg of steam at 9 bar and 90% quality. The space above the piston, initially 0.05m3, contains air at 300 K to maintain the pressure on the steam. Additional air is forced into the upper chamber, forcing the piston down and increasing the steam pressure until the steam has 100% quality. The final steam pressure is 30 bars, and the work done on the steam is 360 kJ, but the air above the steam has not had time to exchange heat with the piston, cylinder, or surroundings. The air supply line is at 50 bar and 300 K. What is the final temperature of the air in the upper chamber? (ANS. online)
P4.19. A well-insulated cylinder, fitted with a frictionless piston, initially contained 9 kg of liquid water and 0.4 kg of water vapor at a pressure of 1.4 MPa. 2 kg of steam at 1.6 MPa was admitted to the cylinder while the pressure was held constant by allowing the piston to expand. (ANS. online)
a. Write the energy balance for this process.
b. If the final volume of the contents of the cylinder was six times the initial volume, determine the temperature of the superheated steam that was admitted to the cylinder.
P4.20. Many action movies show gas cylinders that have their caps knocked off. The tanks go flying around wreaking havoc (only on the bad guys, of course). How much velocity could a tank like that really generate? For an upper bound, consider a tank traveling horizontally on a frictionless surface with an isentropic nozzle taking the place of the cap that has been knocked off. Suppose the cylinder weighs 70 kg and holds 50 L of He at 100bar, 300 K.
a. Write the most appropriate energy balance(s) for this process. Clearly identify the system(s) pertaining to your energy balance(s). Explain your reasoning briefly.
b. Write the most appropriate entropy balance(s) for this process. Clearly identify the system(s) pertaining to your entropy balance(s). Explain your reasoning briefly.
c. Solve for the total kinetic energy (MJ) developed by the tank and its velocity.
Leave a Reply