In Chapter 2 we used the energy balance to track energy changes of the system by the three types of interactions with the surroundings—flow, heat, and work. This method was extremely helpful because we could use the balance as a checklist to account for all interactions. Therefore, we present a general entropy balance in the same manner. To solve a process problem we can use an analogous balance approach of starting with an equation including all the possible contributions that might occur and eliminating the balance terms that do not apply for the situation under consideration.
Entropy change within a system boundary will be given by the difference between entropy which is transported in and out, plus entropy changes due to the heat flow across the boundaries, and in addition, since entropy may be generated by an irreversible process, an additional term for entropy generation is added. A general entropy balance is

Like the energy balance, the quantity to the left of the equals sign represents the entropy change of the system. The term representing heat transfer should be applied at each location where heat is transferred and the Tsys for each term is the system temperature at each boundary where the heat transfer occurs. The heat transfer represented in the general entropy balance is the heat transfer which occurs in the actual process. We may simplify the balance for steady-state or closed systems:


![]() Open, steady-state entropy balance.
Open, steady-state entropy balance.
![]() Closed system entropy balance.
Closed system entropy balance.
The heat flow term(s) are always written in the balance with a “plus” from the perspective of the system for which the balance is written.
The entropy balance provides us with an additional equation which may be used in solving thermodynamic problems; however, in irreversible processes, the entropy generation term usually cannot be calculated from first principles. Thus, it is an unknown in Eqns. 4.32–4.34. The balance equation is not useful for calculating any other unknowns when Sgen is unknown. In Example 4.8 the problem would have been difficult if we applied the entropy balance to the water or the surroundings independently, because we did not know how to calculate Sgen for each subsystem. However, we could calculate ΔS for each subsystem along reversible pathways. Summing the entropy changes for the subsystems of the universe, we obtain the entropy change of the universe. Consider the right-hand side of the entropy balance when written for the universe in this example. There is no mass flow in and out of the universe—it all occurs between the subsystems of the universe. In addition, heat flow also occurs between subsystems of the universe, and the first three terms on the right-hand side of the entropy balance are zero. Therefore, the entropy change of the universe is equal to the entropy generated in the universe.
The criterion for the feasibility of a process is that the entropy generation term must be greater than or equal to zero. The feasibility may not be determined unequivocally by ΔS for the system unless the system is the universe.
Note: As we work examples for irreversible processes, note that we do not apply the entropy balance to find entropy changes. We always calculate entropy changes by alternative reversible pathways that reach the same states, then we apply the entropy balance to find how much entropy was generated.
Alternatively, for reversible processes, we do apply the entropy balance because we set the entropy generation term to zero.
Let us now apply the entropy balance—first to another heat conduction problem. In Example 4.8 we studied an unsteady-state system. Now let us consider steady-state heat transfer to show which entropy balance terms are important in this application. In this example, we show that such heat conduction results in entropy generation because entropy generation occurs where the temperature gradient exists.
Example 4.9. Entropy balances for steady-state composite systems
Imagine heat transfer occurring between two reservoirs.
a. A steady-state temperature profile for such a system is illustrated in Fig. (a) below. (Note that the process is an unsteady state with respect to the reservoirs, but the focus of the analysis here is on the wall.) The entire temperature gradient occurs within the wall. In this ideal case, there is no temperature gradient within either reservoir (therefore, the reservoirs are not a source of entropy generation). Note that the wall is at steady state. Derive the relevant energy and entropy balances, carefully analyzing three subsystems: the hot reservoir, the cold reservoir, and the wall. Note that a superficial view of the reservoirs and wall is shown in Fig. (b).
b. Suppose the wall was replaced by a reversible Carnot engine across the same reservoirs, as illustrated in Fig. (c). Combine the energy and entropy balances to obtain the thermal efficiency.
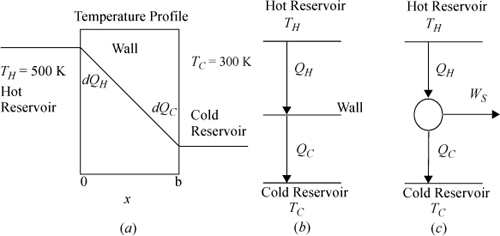
Note: Keeping track of signs and variables can be confusing when the universe is divided into multiple subsystems. Heat flow on the hot side of the wall will be negative for the hot reservoir, but positive for the wall. Since the focus of the problem is on the wall or the engine, we will write all symbols from the perspective of the wall or engine and relate to the reservoirs using negative signs and subscripts.
Solution
a. Since the wall is at steady state, the energy balance for the wall shows that the heat flows in and out are equal and opposite:
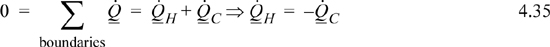
The entropy balance in each reservoir simplifies:
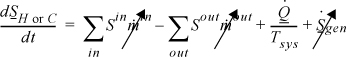
The entropy generation term drops out because there is no temperature gradient in the reservoirs. Taking the hot reservoir as the subsystem and noting that we have defined QH and QC to be based on the wall, we write:
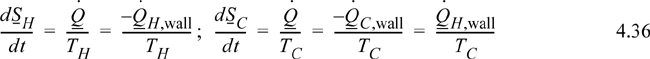
where the heat fluxes are equated by the energy balance.
Now consider the entropy balance for the wall subsystem. Entropy is a state property, and since no state properties throughout the wall are changing with time, entropy of the wall is constant, and the left-hand side of the entropy balance is equal to zero. Note that the entropy generation term is kept because we know there is a temperature gradient:
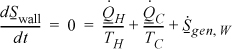
Noting the relation between the heat flows in Eqn. 4.35, we may then write for the wall:

Then the wall with the temperature gradient is a source of entropy generation. Summarizing,
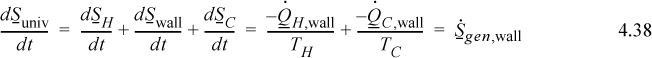
Hence we see that the wall is the source of entropy generation of the universe, which is positive. Notice that inclusion of the wall is important in accounting for the entropy generation by the entropy balance equations.
b. The overall energy balance relative for the engine is:
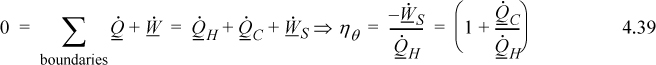
![]() Entropy is generated by a temperature gradient.
Entropy is generated by a temperature gradient.
The the engine operates a steady-state cycle, dSengine/dt = 0 (it is internally reversible):
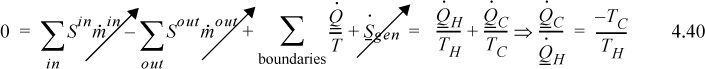
As before, ![]() and we have derived it using the entropy balance. Note that the heat flows are no longer equal and are such that the entropy changes of the reservoirs sum to zero.
and we have derived it using the entropy balance. Note that the heat flows are no longer equal and are such that the entropy changes of the reservoirs sum to zero.
We have concluded that heat transfer in a gradient results in entropy production. How can we transfer heat reversibly? If the size of the gradient is decreased, the right-hand side of Eqn. 4.37 decreases in magnitude; coincidentally, heat conduction slows, through the following relation:16
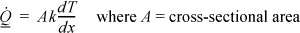
A smaller temperature gradient decreases the rate of production of entropy, but from a practical standpoint, it requires a longer time to transfer a fixed amount of heat. If we wish to transfer heat reversibly from two reservoirs at finitely different temperatures, we must use a heat engine, as described in part (b). In addition to transferring the heat reversibly, use of a heat engine generates work.
Summary: This example has shown that boundaries (walls) between systems can generate entropy. In this example, entropy was not generated in either reservoir because no temperature profile existed. The entropy generation occurred within the wall.
![]() Entropy may be generated at system boundaries.
Entropy may be generated at system boundaries.
Note that we could have written the engine work of part (b) as follows:
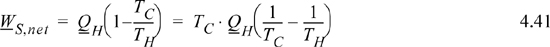
Compare this to Eqn. 4.37, the result of the steady-state entropy generation. If we run the heat transfer process without obtaining work, then the universe loses a quantity of work equal to the following:

Note that TC, the colder temperature of our engine, is important in relating the entropy generation to the lost work. TC can be called the temperature at which the work is lost. Lost work is explored more completely in Section 4.12. Also note that we have chosen to operate the heat engine at temperatures which match the reservoir temperatures. This is arbitrary, but is required to obtain the maximum amount of work. The heat engine may be reversible without this constraint, but the entire process will not be reversible. These details are clarified in the next section.
An entirely analogous analysis of heat transfer would apply if we ran the heat engine in reverse, as a heat pump. Only the signs would change on the direction the heat and work were flowing relative to the heat pump. Therefore, the use of entropy permits us to reiterate the Carnot formulas in the context of all fluids, not just ideal gases.
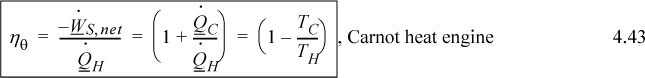
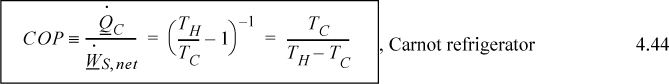
![]() Carnot coefficient of performance.
Carnot coefficient of performance.
4.5. Internal Reversibility
A process may be irreversible due to interactions at the boundaries (such as discussed in Example 4.9 on page 155) even when each system in the process is reversible. Such a process is called internally reversible. Such a system has no entropy generation inside the system boundaries. We have derived equations for Carnot engines and heat pumps, assuming that the devices operate between temperatures that match the reservoir temperatures. While such restrictions are not necessary for internal reversibility, we show here that the work is maximized in a Carnot engine at these conditions and minimized in a Carnot heat pump. Note that in development of the Carnot devices, the only temperatures of concern are the operating temperatures at the hot and cold portions of the cycle. In the following illustrations, the internally reversible engine or pump operates between TH and TC, and the reservoir temperatures are T2 and T1.
Heat Engine
A schematic for a Carnot engine is shown in Fig 4.5(a). Heat is being transferred from the reservoir at T2 to the reservoir at T1, and work is being obtained as a result. In order for heat transfer to occur between the reservoirs and the heat engine in the desired direction, we must satisfy T2 ≥ TH >TC≥T1, and since the thermal efficiency is given by Eqn. 3.6, for maximum efficiency (maximum work), TC should be as low as possible and TH as high as possible, i.e., set TH = T2, TC = T1.

Figure 4.5. Schematic of a heat engine (a) and heat pump (b). The temperatures of the reservoirs are not required to match the reversible engine temperatures, but work is optimized if they do, as discussed in the text.
![]() The operating temperatures of a reversible heat engine or heat pump are not necessarily equal to the surrounding’s temperatures; however, the optimum work interactions occur if they match the surrounding’s temperature because matching the temperatures eliminates the finite temperature-driving force that generates entropy.
The operating temperatures of a reversible heat engine or heat pump are not necessarily equal to the surrounding’s temperatures; however, the optimum work interactions occur if they match the surrounding’s temperature because matching the temperatures eliminates the finite temperature-driving force that generates entropy.
Heat Pump
A schematic for a Carnot heat pump is shown in Fig. 4.5(b). Heat is being transferred from a reservoir at T1 to the reservoir at T2, and work is being supplied to achieve the transfer. In order for heat transfer to occur between the reservoirs and the heat engine in the desired direction, we must satisfy T2 ≤ TH > TC ≤ T1. Since the COP is given by Eqn. 4.44, for maximum COP (minimum work), TC should be as high as possible and TH as low as possible, i.e., set TC = T1, TH = T2. Therefore, optimum work interactions occur when the Carnot device operating temperatures match the surrounding temperatures. We use this feature in future calculations without special notice.
Leave a Reply