Chapters 2 and 3 showed the importance of irreversibility when it comes to efficient energy transformations. We noted that prospective work energy was generally dissipated into thermal energy (stirring) when processes were conducted irreversibly. If we only had an “irreversibility meter,” we could measure the irreversibility of a particular process and design it accordingly. Alternatively, we could be given the efficiency of a process relative to a reversible process and infer the magnitude of the irreversibility from that. For example, experience might show that the efficiency of a typical 1000 kW turbine is 85%. Then, characterizing the actual turbine would be simple after solving for the reversible turbine (100% efficient).
In our initial encounters, entropy generation provides this measure of irreversibility. Upon studying entropy further, however, we begin to appreciate its broader implications. These broader implications are especially important in the study of multicomponent equilibrium processes, as discussed in Chapters 8–16. In Chapters 5–7, we learn to appreciate the benefits of entropy being a state property. Since its value is path independent, we can envision various ways of computing it, selecting the path that is most convenient in a particular situation.
Entropy may be contemplated microscopically and macroscopically. The microscopic perspective favors the intuitive connection between entropy and “disorder.” The macroscopic perspective favors the empirical approach of performing systematic experiments, searching for a unifying concept like entropy. Entropy was initially conceived macroscopically, in the context of steam engine design. Specifically, the term “entropy” was coined by Rudolf Clausius from the Greek for transformation.1 To offer students connections with the effect of volume (for gases) and temperature, this text begins with the microscopic perspective, contemplating the detailed meaning of “disorder” and then demonstrating that the macroscopic definition is consistent.
![]() Entropy is a useful property for determining maximum/minimum work.
Entropy is a useful property for determining maximum/minimum work.
Rudolf Julius Emanuel Clausius (1822–1888), was a German physicist and mathematician credited with formulating the macroscopic form of entropy to interpret the Carnot cycle and developed the second law of thermodynamics.
To appreciate the distinction between the two perspectives on entropy, it is helpful to define the both perspectives first. The macroscopic definition is especially convenient for solving problems process problems, but the connection between this definition and disorder is not immediately apparent.
Macroscopic definition—Intensive entropy is a state property of the system. For a differential change in state of a closed simple system (no internal temperature gradients or composition gradients and no internal rigid, adiabatic, or impermeable walls),2 the differential entropy change of the system is equal to the heat absorbed by the system along a reversible path divided by the absolute temperature of the system at the surface where heat is transferred.

where dS is the entropy change of the system. We will later show that this definition is consistent with the microscopic definition.
Microscopic definition—Entropy is a measure of the molecular disorder of the system. Its value is related to the number of microscopic states available at a particular macroscopic state. Specifically, for a system of fixed energy and number of particles, N,
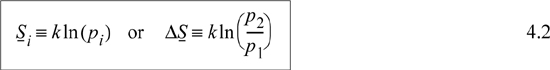
where pi is the number of microstates in the ith macrostate, k = R/NA. We define microstates and macrostates in the next section.
The microscopic perspective is directly useful for understanding how entropy changes with volume (for a gas), temperature, and mixing. It simply states that disorder increases when the number of possible arrangements increases, like the socks and drawers mentioned in the introduction. Similarly, molecules redistribute themselves when a valve is opened until the pressures have equilibrated. From the microscopic approach, entropy is a specific mathematical relation related to the number of possible arrangements of the molecule. Boltzmann showed that this microscopic definition is entirely consistent with the macroscopic property inferred by Rudolf Clausius. We will demonstrate how the approaches are equivalent.
Entropy is a difficult concept to understand, mainly because its influence on physical situations is subtle, forcing us to rely heavily on the mathematical definition. We have ways to try to make some physical connection with entropy, and we will discuss these to give you every opportunity to develop a sense of how entropy changes. Ultimately, you must reassure yourself that entropy is defined mathematically, and like enthalpy, can be used to solve problems even though our physical connection with the property is occasionally less than satisfying.
In Section 4.2, the microscopic definition of entropy is discussed. On the microscopic scale, S is influenced primarily by spatial arrangements (affected by volume and mixing), and energetic arrangements (occupation) of energy levels (affected by temperature). We clarify the meaning of the microscopic definition by analyzing spatial distributions of molecules. To make the connection between entropy and temperature, we outline how the principles of volumetric distributions extend to energetic distributions. In Section 4.3, we introduce the macroscopic definition of entropy and conclude with the second law of thermodynamics.
![]() The microscopic approach to entropy is discussed first, then the macroscopic approach is discussed.
The microscopic approach to entropy is discussed first, then the macroscopic approach is discussed.
The second law is formulated mathematically as the entropy balance in Section 4.4. In this section we demonstrate how heat can be converted into work (as in an electrical power plant). However, the maximum thermal efficiency of the conversion of heat into work is less than 100%, as indicated by the Carnot efficiency. The thermal efficiency can be easily derived using entropy balances. This simple but fundamental limitation on the conversion of heat into work has a profound impact on energy engineering. Section 4.5 is a brief section, but makes the key point that pieces of an overall process can be reversible, even while the overall process is irreversible.
In Section 4.6 we simplify the entropy balance for common process equipment, and then use the remaining sections to demonstrate applications of system efficiency with the entropy balance. Overall, this chapter provides an understanding of entropy which is essential for Chapter 5 where entropy must be used routinely for process calculations.
Leave a Reply