An open-system that does not meet the requirements of a steady-state system is called an unsteady-state open-system as shown in Fig. 2.5. The mass-in may not equal the mass-out, or the system state variables (e.g., temperature) may change with time, so the system itself may gain in internal energy, kinetic energy, or potential energy. An example of this is the filling of a tank being heated with a steam jacket. Another example is the inflation of a balloon, where there is mass flow in and the system boundary expands. These considerations lead to a general equation which is applicable to open or closed systems,
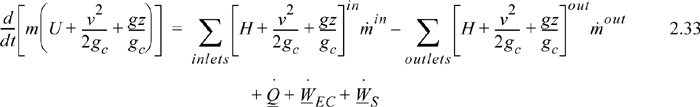
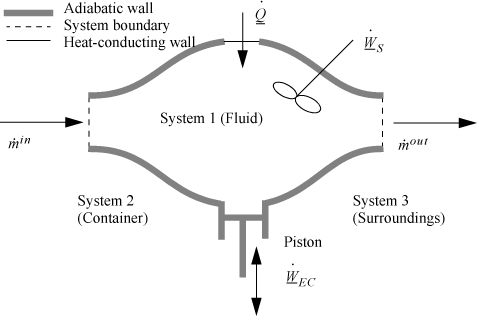
Figure 2.5. Schematic of a general system.
where the heat and work interactions are summations of the individual heat and work interactions over all boundaries. We also may write this with the time dependence implied:
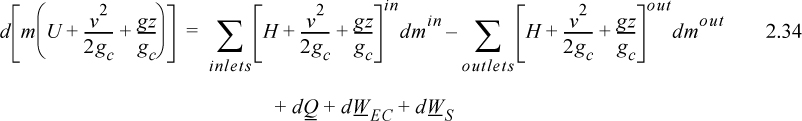
Note: The signs and conventions are the same as presented following Eqn. 2.24.
Usually, the closed-system or the steady-state equations are sufficient by themselves. But for unsteady-state open systems, the entire equation must be considered. Fortunately, even when the entire energy balance is applied, some of the terms are usually not necessary for a given problem, so fewer terms are usually needed than shown in Eqn. 2.33. An objective of this text is to build your ability to recognize which terms apply to a given problem.
Leave a Reply