Summary

We have seen in this chapter that calculus provides powerful tools permitting us to calculate changes in immeasurable properties in terms of other measurable properties. We started by defining additional convenience functions A, and G by performing Legendre transforms. We then reviewed basic calculus identities and extended throughout the remainder of the chapter. The ability to perform these manipulations lays the foundation for the development of general methods to calculate thermodynamic properties for any chemical from P–V–T relations. If we only had a general relation that perfectly described P=P(V,T) for all the chemicals in the universe, it could be combined with the tools in this chapter to compute any property required by the energy and entropy balances. At present, no such perfect equation exists. This means that we need to understand what makes it so difficult to develop such an equation and how the various available equations can be applied in various situations to achieve reasonable and continuously improving estimates.

Important Equations

The procedures developed in this chapter are what is important. They provide a basis for transforming one set of derivatives into another and for thinking systematically about how variables relate to one another. The basic identities 6.11–6.17 combine with the fundamental properties for the remainder of the chapter. Nevertheless, several equations stand out as a summary of the results that can be rearranged to a desired form relatively quickly. These are the Maxwell Eqns. 6.29–6.32, and also some intermediate manipulations 6.37–6.41. They are included on the front flap of the text-book for your convenience. Eqn. 6.47 stands out as an equation for long term reference because it relates the Helmholtz energy to the internal energy. That is a key step when we turn to consideration of solution models. Also, when combined with a similar relation is for compressibility factor in Chapter 7, the central role of Helmholtz energy in thermodynamic properties becomes apparent.

Test Yourself

1. What are the restrictions necessary to calculate one state property in terms of only two other state variables?

2. When integrating Eqn. 6.53, under what circumstances may C_V be taken out of the integral?

3. May Eqn. 6.53 be applied to a condensed phase?

4. Is the heat capacity different for liquid acetone than for acetone vapor?

5. Can the tabulated heat capacities be used in Eqn. 6.53 for gases at high pressure?

6.5. Practice Problems

P6.1. Express in terms of P, V, T, C_P, C_V, and their derivatives. Your answer may include absolute values of S if it is not a derivative constraint or within a derivative.

a. (∂H/∂S)_V

b. (∂H/∂P)_V

c. (∂G/∂H)_P

(ANS. (a) T[1+V/C_V(∂P/∂T)_v] (b) C_v(∂T/∂P)_v+V (c) –S/C_P)

6.6. Homework Problems

6.1. CO₂ is given a lot of credit for global warming because it has vibrational frequencies in the infrared (IR) region that can absorb radiation reflected from the Earth and degrade it into thermal energy. The vibration at ε/k = 290K (903cm^—1) is particularly important.

a. Plot C_v^ig/R versus T for CO₂ in the range 200—400 K. Use the polynomial expression in the back of the book to estimate C_v^ig/R at 200 K as a reference. Also plot the polynomial expression on the same chart as a dashed line.

b. Use your Internet search skills to learn the wavelength range of the IR spectrum. How many wavelengths are there? What fraction does the wavelength at 903cm^—1 comprise? If the Earth’s atmosphere was composed entirely of CO₂, what fraction of IR energy could be absorbed by CO₂?

c. The Earth’s atmosphere is really 380ppm CO₂. If the absorption efficiency is proportional to the concentration, how much IR energy could be absorbed by CO₂ in this case?

6.2. Express in terms of P, V, T, C_P, C_V, and their derivatives. Your answer may include absolute values of S if it is not a derivative constraint or within a derivative.

a. (∂G/∂P)_T

b. (∂P/∂A)_V

c. (∂T/∂P)_S

d. (∂H/∂T)_U

e. (∂T/∂H)_S

f. (∂A/∂V)_P

g. (∂T/∂P)_H

h. (∂A/∂S)_P

i. (∂S/∂P)_G

6.3. Express the following in terms of U, H, S, A, and their derivatives.

6.4.

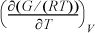
a. Derive  and  in terms of measurable properties.

b. dH = dU + d(PV) from the definition of H. Apply the expansion rule to show the difference between  and  is the same as the result from part (a).

6.5. In Chapter 2, internal energy of condensed phases was stated to be more weakly dependent on pressure than enthalpy. This problem evaluates that statement.

a. Derive  and  in terms of measurable properties.

b. Evaluate  and compare the magnitude of the terms contributing to  for the fluids listed in problem 5.6.

c. Evaluate  for the fluids listed in problem 5.6 and compare with the values of .

6.6. Express  in terms of α_P and/or κ_T.

6.7. Express the adiabatic compressibility, , in terms of measurable properties.

6.8. Express the Joule-Thomson coefficient in terms of measurable properties for the following:

a. Van der Waals equation given in Example 6.6

b. An ideal gas.

6.9.

a. Prove .

b. For an ideal gas along an adiabat, (P/Pⁱ) = (T/Tⁱ)^Cp^/R. Demonstrate that this equation is consistent with the expression from part (a).

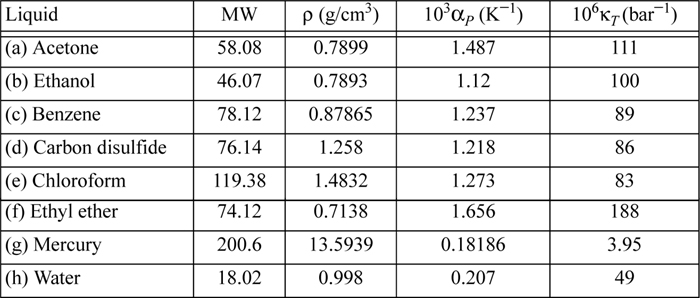
6.10. Determine the difference C_P – C_V for the following liquids using the data provided near 20°C.

6.11. A rigid container is filled with liquid acetone at 20°C and 1 bar. Through heat transfer at constant volume, a pressure of 100 bar is generated. C_P = 125 J/mol-K. (Other properties of acetone are given in problem 6.10.) Provide your best estimate of the following:

a. The temperature rise

b. ΔS, ΔU, and ΔH

c. The heat transferred per mole

6.12. The fundamental internal energy relation for a rubber band is dU = TdS – FdL where F is the system force, which is negative when the rubber band is in tension. The applied force is given by F_applied = k(T)(L – L₀) where k(T) is positive and increases with increasing temperature. The heat capacity at constant length is given by C_L = α(L) + β(L)·T. Stability arguments show that α(L) and β(L) must provide for C_L ≥ 0.

a. Show that temperature should increase when the rubber band is stretched adiabatically and reversibly.

b. Prof. Lira in his quest for scientific facts hung a weight on a rubber band and measured the length in the laboratory at room temperature. When he hung the rubber band with the same weight in the refrigerator, he noticed that the length of the rubber band had changed. Did the length increase or decrease?

c. The heat capacity at constant force is given by

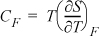
Derive a relation for C_F – C_L and show whether this difference is positive, negative, or zero.

d. The same amount of heat flows into two rubber bands, but one is held at constant tension and the other at constant length. Which has the largest increase in temperature?

e. Show that the dependence of k(T) on temperature at constant length is related to the dependence of entropy on length at constant temperature. Offer a physical description for the signs of the derivatives.CopycopyHighlighthighlightAdd NotenoteGet Linklink