Pressure Drop Across a Flow Conduit

The frictional losses due to the flow of fluids result in a decrease of pressure from the point upstream to the point downstream. In other words, a higher upstream pressure is needed to overcome frictional losses in order to transfer fluid from the point upstream to the point downstream. The pressure drop can be viewed as the potential that induces fluid flow, analogous to voltage in an electrical circuit. Different mathematical expressions are used to obtain this pressure drop for the two different flow regimes.

The following equation shows the pressure drop for laminar flow through a pipe with constant circular cross section of diameter d:

In this equation, ΔP is the pressure drop over pipe length L when the volumetric flow rate is Q. Equation 5.6 is called the Hagen-Poiseuille equation [1] in honor of G. Hagen and J. L. Poiseuille, who developed this formulation.

For turbulent flow, the pressure drop is given by the following:

where f is the friction factor³, which is a function of the Reynolds number. Figure 5.3 shows the generalized trend exhibited by the friction factor as a function of the Reynolds number [3]. The friction factor, in the turbulent regimes, also shows a dependence on the roughness of the pipe, as indicated by the value of the parameter k/D in the figure.

3. The friction factor, as used here and by chemical engineers generally, is the Fanning friction factor. Mechanical and civil engineers often use the Darcy friction factor, which, while calculated differently, has the same physical significance.

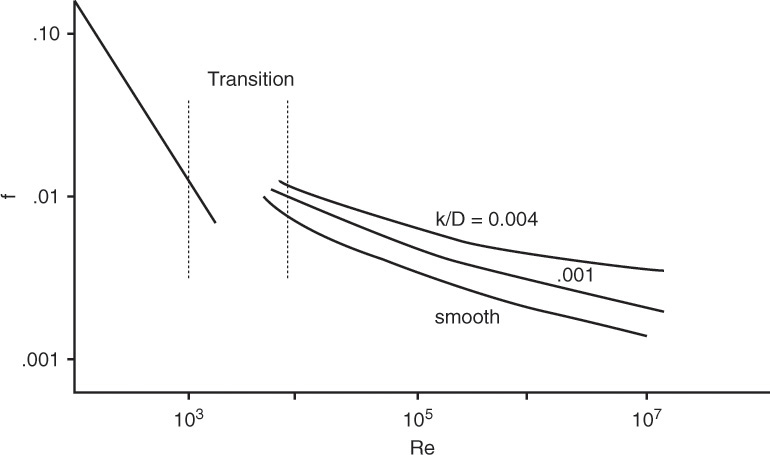
Figure 5.3 A generalized friction factor plot.

Source: Thomson, W. J., Introduction to Transport Phenomena, Prentice Hall, Upper Saddle River, New Jersey, 2000.

Chemical engineers often use the Nikuradse equation (covered in Chapter 4, “Introduction to Computations in Chemical Engineering”) for calculating the friction factor for turbulent flow through smooth pipes:

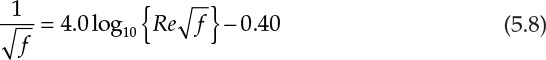
This equation is valid for flows having Re between 4000 and 3.2 × 10⁶. The pressure drop so obtained is used further in the mechanical energy balance equation to calculate the power requirements for pumping the fluid.