P7.1. For Tr < 1 and Pr ≈ Prsat, the Peng-Robinson equation of state has three roots corresponding to compressibility factors between zero and 10. The smallest root is the compressibility factor of the liquid. The largest root is the compressibility factor of the vapor and the middle root has no physical significance. This gives us a general method for finding the compressibility factor of any fluid obeying the Peng-Robinson equation. For the iterative method, use an initial guess of Z = 0 to find the liquid roots and Z = 1 to find the vapor roots of methane at the following conditions:
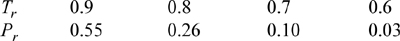
Compare to experimental data from N.B. Vargaftik. 1975. Handbook of Physical Properties of Liquids and Gases, 2nd ed., New York: Hemisphere.

ANS. The liquid roots are very close. The vapor roots are accurate for Tr < 0.9.
a. Estimate the value of the compressibility factor, Z, for neon at Pr = 30 and Tr = 15.
b. Estimate the density of neon at Pr = 30 and Tr = 15. (ANS. 1.14, 0.25 g/cm3)
P7.3. Above the critical point or far from the saturation curve,21 only one real root to the cubic equation exists. If we are using Newton’s method, we can check how many phases exist by trying the two different initial guesses and seeing if they both converge to the same root. If they do, then we can assume that only one real root exists. Find the compressibility factors for methane at the following conditions, and identify whether they are vapor, liquid, or supercritical fluid roots. Complete the table. Compare your results to Z-charts.
When Newton’s method is applied with an initial guess of zero, erratic results are obtained at these conditions. Explain what is happening, and why, by plotting F(Z) versus Z for each iteration.
P7.4. A rigid vessel is filled to one-half its volume with liquid methane at its normal boiling point (111 K). The vessel is then closed and allowed to warm to 77°F. Calculate the final pressure using the Peng-Robinson equation. (ANS. 33.8 MPa)
P7.5. 4 m3 of methane at 20°C and 1 bar is roughly equivalent to 1 gal of gasoline in an automotive engine of ordinary design. If methane were compressed to 200 bar and 20°C, what would be the required volume of a vessel to hold the equivalent of 10 gal of gasoline? (ANS. 16 L)
P7.6. A carbon dioxide cylinder has a volume of 0.15 m3 and is filled to 100 bar at 38°C. The cylinder cools to 0°C. What is the final pressure in the cylinder and how much more CO2 can be added before the pressure exceeds 100 bar? If you add that much CO2 to the cylinder at 0°C, what will the pressure be in the cylinder on a hot, 38°C day? What will happen if the cylinder can stand only 200 bar? [Hint: log (Prsat) ≈ (7(1 + ω)/3) (1 – 1/Tr)] (ANS. 3.5 MPa, 38 MPa, boom!)
7.14. Homework Problems
7.1. The compressibility factor chart provides a quick way to assess when the ideal gas law is valid. For the following fluids, what is the minimum temperature in K where the fluid has a gas phase compressibility factor greater than 0.95 at 30 bar?
a. Nitrogen
b. Carbon dioxide
c. Ethanol
7.2. A container having a volume of 40 L contains one of the following fluids at the given initial conditions. After a leak, the temperature and pressure are remeasured. For each option, determine the kilograms of fluid lost due to the leak, using:
a. Compressibility factor charts
b. The Peng-Robinson equation
Options:
i. Methane Ti = 300 K, Pi = 100 bar, Tf = 300 K, Pf = 50 bar
ii. Propane Ti = 300 K, Pi = 50 bar, Tf = 300 K, Pf = 0.9 bar
iii. n-butane Ti = 300 K, Pi = 50 bar, Tf = 300 K, Pf = 10 bar
7.3. Estimate the liquid density (g/cm3) of propane at 298 K and 10 bar. Compare the price per kilogram of propane to the price per kilogram of regular gasoline assuming the cost of 5 gal of propane for typical gas grills is roughly $20. The density of regular gasoline can be estimated by treating it as pure isooctane (2,2,4-trimethylpentane ρ = 0.692 g/cm3) at 298 K and 1 bar.
7.4. From experimental data it is known that at moderate pressures the volumetric equation of state may be written as PV = RT + B · P, where the second virial coefficient B is a function of temperature only. Data for methane are given by Dymond and Smith (1969) as,22

a. Identify the Boyle temperature (the temperature at which B = 0) and the inversion temperature (the temperature at which (∂T/∂P)H = 0) for gaseous methane. [Hint: Plot B versus T–1 and regress a trendline, then differentiate analytically.]
b. Plot these data versus T–1 and compare to the curve generated from Eqn. 7.7. Use points without lines for the experimental data and lines without points for the theoretical curve.
7.5. Data for hydrogen are given by Dymond and Smith (1969) as,

a. Plot these data versus T–1and compare to the results from the generalized virial equation (Eqn. 7.7). Suggest a reason that this specific compound does not fit the generalized equation very accurately. Use points without lines for the experimental data and lines without points for the theoretical curve.
b. Use the generalized virial equation to speculate whether a small leak in an H2 line at 300 bar and 298 K might raise the temperature of H2 high enough to cause it to spontaneously ignite.
7.6. N.B. Vargaftik (1975)23 lists the following experimental values for the specific volume of isobutane at 175°C. Compute theoretical values and their percent deviations from experiment by the following:
a. The generalized charts
b. The Peng-Robinson equation

7.7. Evaluate (∂P/∂V)T for the equation of state where b is a constant:
P = RT/(V – b)
7.8. Evaluate (∂P/∂T)V for the equation of state where a and b are constants:
P = RT/(V = b) + a/T3/2
7.9. Evaluate ![]() for the Redlich-Kwong equation of state
for the Redlich-Kwong equation of state ![]() , where a and b are temperature-independent parameters.
, where a and b are temperature-independent parameters.
a. The derivative (∂V/∂T)P is tedious to calculate by implicit differentiation of an equation of state such as the Peng-Robinson equation. Show that calculus permits us to find the derivative in terms of derivatives of pressure, which are easy to find, and provide the formula for this equation of state.
b. Using the Peng-Robinson equation, calculate the isothermal compressibility of ethylene for saturated vapor and liquid at the following conditions: {Tr = 0.7, P = 0.414 MPa}; {Tr = 0.8, P = 1.16 MPa}; {Tr = 0.9, P = 2.60 MPa}.
7.11. When cubic equations of state give three real roots for Z, usually the smallest root is the liquid root and the largest is the vapor root. However, the Peng-Robinson equation can give real roots at high pressure that differ from this pattern. To study this behavior, tabulate all the roots found for the specified gas and pressures. As the highest pressures are approached at this temperature, is the fluid a liquid or gas? Which real root (smallest, middle, or largest) represents this phase at the highest pressure, and what are the Z values at the specified pressures?
a. Ethylene at 250 K and 1, 3, 10, 100, 150, 170, 175, and 200 MPa
b. n-Hexane at 400 K and 0.2, 0.5, 1, 10, 100, 130 and 150 MPa
c. Argon at 420 K and 0.1, 1, 5, and 10 MPa
7.12. Plot Pr versus ρr for the Peng-Robinson equation with Tr = [0.7,0.9,1.0], showing both vapor and liquid roots in the two-phase region. Assume ω = 0.040 as for N2. Include the entire curve for each isotherm, as illustrated in Fig. 7.1 on page 254. Also show the horizontal line that connects the vapor and liquid densities at the saturation pressure. Use lines without points for the theoretical curves. Estimate Trsat by log(Prsat) = 2.333(1 + ω) (1 – 1/Trsat).
7.13. Within the two-phase envelope, one can draw another envelope representing the limits of supercooling of the vapor and superheating of liquid that can be observed in the laboratory; along each isotherm these are the points for which (∂P/∂ρ)T = 0. Obtain this envelope for the Peng-Robinson equation, and plot it on the same figure as generated in problem 7.12. This is the spinodal curve. The region between the saturation curve and the curve just obtained is called the metastable region of the fluid. Inside the spinodal curve, the fluid is unconditionally unstable. The saturation curve is called the binodal curve. Outside, the fluid is entirely stable. It is possible to enter the metastable region with hot water by heating at atmospheric pressure in a very clean flask. Sooner or later, the superheated liquid becomes unstable, however. Describe what would happen to your flask of hot water under these conditions and a simple precaution that you might take to avoid these consequences.
7.14. Develop a spreadsheet that computes the values of the compressibility factor as a function of reduced pressure for several isotherms of reduced temperature using the Lee-Kesler (1975) equation of state (AIChE J., 21:510). A tedious but straightforward way to do this is to tabulate reduced densities from 0.01 to 10 in the top row and reduced temperatures in the first column. Then, enter the Lee-Kesler equation for the compressibility factor of the simple fluid in one of the central cells and copy the contents of that cell to all other cells in the table. Next, copy that entire table to a location several rows lower. Replace the contents of the new cells by the relation Pr = Z·ρr·Tr. You now have a set of reduced pressures corresponding to a set of compressibility factors for each isotherm, and these can be plotted to reproduce the chart in the chapter, if you like. Copy this spreadsheet to a new one, and change the values of the B, C, D, and E parameters to correspond to the reference fluid. Finally, copy the simple fluid worksheet to a new worksheet, and replace the contents of the compressibility factor cells by the formula: Z = Z0 + ω(Zref – Z0)/ωref, where the Zref and Z0 refer to numbers in the cells of the other worksheets.
7.15. The Soave-Redlich-Kwong equation24 is given by:
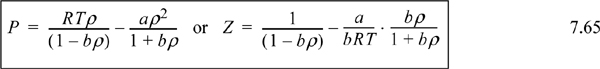
where ρ = molar density = n/V

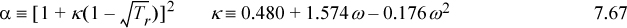
Tc, Pc, and ω are reducing constants according to the principle of corresponding states. Solve for the parameters at the critical point for this equation of state (ac, bc, and Zc) and list the next five significant figures in the sequence 0.08664…….
7.16. Show that Bc = bPc/RTc = 0.07780 for the Peng-Robinson equation by setting up the cubic equation for Bc analogous to the van der Waals equation and solving analytically as described in Appendix B.
7.17. Determine the values of ε/kTc, Zc, and bc in terms of Tc and Pc for the equation of state given by

where F = exp(ε/kT) – 1. The first term on the right-hand side is known as the Scott equation for the hard-sphere compressibility factor.
7.18. Consider the equation of state
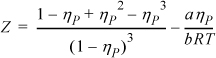
where ηP = b/V. The first term on the right-hand side is known as the Carnahan-Starling equation for the hard-sphere compressibility factor.
a. Determine the relationships between a, b, and Tc, Pc, Zc.
b. What practical restrictions are there on the values of Zc that can be modeled with this equation?
7.19. The ESD equation of state25 is given by
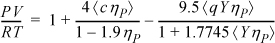
ηP = bρ, c is a “shape parameter” which represents the effect of non-sphericity on the repulsive term, and q = 1 + 1.90476(c – 1). A value of c = 1 corresponds to a spherical molecule. Y is a temperature-dependent function whose role is similar to the temperature dependence of the a parameter in the Peng-Robinson equation. Use the methods of Example 7.7 to fit b and Y to the critical point for ethylene using c = 1.3.
7.20. A molecular simulation sounds like an advanced subject, but it is really quite simple for hard spheres.26 Furthermore, modern software is readily available to facilitate performing simulations, after an understanding of the basis for the simulations has been demonstrated. This problem provides an opportunity to demonstrate that understanding. Suppose that four hard disks are bouncing in two dimensions around a square box. Let the diameters of the disks, σ, be 0.4 nm, masses be 40 g/mole, and length of the square box, L, be 5 nm. Start the four disks at (0.25L, 0.25L), (0.75L, 0.25L), (0.25L, 0.75L), (0.75L, 0.75L) and with initial velocities of (v, v/(1 + 2½)), (–v, v), (v/2½, – v/2½), (–v/2½, – v/2½), where v designates an arbitrary velocity. (Hint: you may find useful information in the DMD module at Etomica.org.)
a. Compute v initially assuming a temperature of 298 K.
b. Sum the velocities of all four particles (x and y separately). Explain the significance of these sums.
c. Sketch the disks using arrows to show their directions. Make the sizes of the arrows proportional to the magnitudes of their velocities.
d. Solve for the time of the first collision. Is it with a wall or between particles? Compute the velocities of all disks after the first collision.
7.21. Suppose you had a program to simulate the motions of four molecules moving in 2D slowly enough that you could clearly see the velocities of all disks. (Hint: The Piston-Cylinder applet in the DMD module at Etomica.org is an example of such a program when kept in “adiabatic” mode.)
a. Let the disk interactions be characterized by the ideal gas potential. Describe how the disks would move about. Note that the slow particles would always stay slow, and the fast particles stay fast. Why is that?
b. Change the potential to “repulsion only” as modeled by a hard disk model. Compare the motions of the “repulsion only” particles to the ideal gas particles. Explain the differences. Which seems more realistic?
c. Set the potential to “repulsion and attraction,” as modeled by the square-well model with λ=2.0. Compare the motions of these disks to the “repulsion only” particles and ideal gas particles. Explain the differences.
7.22. Suppose you had a program to simulate the motions of N molecules moving in 2D. (Hint: The 2D applet in the DMD module at Etomica.org is an example of such a program when kept in “adiabatic” mode.)
a. Simulate the motions of the disks using each potential model (ideal gas, hard disk, square well) for 1000 ps (1 picosecond=10–12 second) at a density of 2.86E-6mol/m2 with an initial temperature of 300K. Which would have the higher pressure, ideal gas or hard disks? Explain. Which would have the higher pressure, ideal gas or square well disks? Explain.
b. Simulate the motions of the disks using each potential model for 1000 ps each at a density of 2.86E-6mol/m2 with an initial temperature of 300 K. Sketch the temperature versus time in each case. Explain your observations.
c. Suppose you simulated the motions of the disks using each potential model for 1000 ps each at a density of 2.86E-6mol/m2 with an initial temperature of 300 K. How would the internal energy compare in each case? Explain.
7.23. Sphere and disk collisions can be expressed more compactly and computed more conveniently in vector notation. Primarily, this involves converting the procedures of Example 7.10 to use the dot product of the relative position and relative velocity. (Hint: You may find useful information in the DMD module at Etomica.org.)
a. Write a vector formula for computing the center to center distance between two disks given their velocities, u, and their positions, r0, at a given time, t0.
b. Write a vector formula for computing the distance of each disk from each wall. (Hint: Use unit vectors x=(1, 0) and y=(0, 1) to isolate vector components.)
c. Noting that energy and momentum must be conserved during a collision, write a vector formula for the changes in velocity of two disks after collision.
Hints: (1) ab=abcosθ. (2) A unit vector with direction of a is: a/a.
d. Write a vector formula for the change in velocity of a disk colliding with a wall.
7.24. Molecular simulation can be used to explore the accuracy and significance of individual contributions to an equation of state. Here we explore how the σ parameter relates to experimental data.
a. Erpenbeck and Wood have reported precise simulation results for hard spheres as listed below. Plot these data and compare the ESD and Carnahan-Starling (CS) equations for hard spheres.

b. According to the CS equation, what value do you obtain for ZHS at ηP=0.392?
c. What value of b corresponds to ηP = 0.392 for Xenon at 22.14 mol/L? What value of σ corresponds to that value of b?
d. The simulation results below have been tabulated at ηP = 0.392. Plot Z versus βε for these data. Estimate the value of βε that corresponds to the saturation temperature.
e. Referring to Xenon on the NIST WebBook, estimate the saturation temperature at 22.14mol/L. Referring to part (d) for the value of βε, estimate the value of ε(J/mol).
f. Plot Z versus 1000/T for the simulation data using your best ε and σ at ηP=0.392. Referring to the “fluid properties” link, plot the isochoric data for Xenon from the NIST WebBook at 22.14mol/L on the same axes.
g. What values of a and b of the vdW EOS match the simulation data of this plot? Compute Zvdw versus 1000/T and show the vdW results as a dashed line on the plot.
h. Using the values of ε and σ from parts (c) and (e), simulate the system “isothermally” at 225 K and 20.0 mol/L for ~400 ps (got pizza?). Use the CS equation to estimate the y-intercept for Z. Plot these points including a trendline with equation. Plot the NIST data for this isochore on the same axes. This represents a prediction of the data at 20.0 mol/L since the parameters were determined at other conditions.
i. Using the values of a and b from part (g), plot the vdW results at 20.0 mol/L as a dashed line on the plot. This represents the vdW prediction.
j. Which model (SW or vdW) matches the experimental trend best? Why?
k. Neither prediction is perfect. Suggest ways that we may proceed to improve the predictions further.
SW results at ηP = 0.392, λ = 2.0.

7.25. Molecular simulation can be used to explore the accuracy and significance of individual contributions to an equation of state. Use the DMD module at Etomica.org to tune Xe’s ε and σ parameters.
a. According to the Carnahan-Starling (CS) model, what value do you obtain for ZHS at ηP=0.375?
b. What value of σ corresponds to ηP = 0.375 for Xe at 22.14 mol/L?
c. The simulation results below have been tabulated at ηP = 0.375, λ = 1.7. Plot Z versus βε for these data. Referring to the NIST WebBook for Xe, estimate the saturation T and Z at 22.14 mol/L. Estimate the value of βε that corresponds to the saturation Z. Estimate the value of ε(J/mol).
d. Plot Z versus 1000/T, using your best ε and σ at ηP = 0.375 and showing the fluid properties (isochoric) data from WebBook.nist.gov at 22.14 mol/L on the same axes.
e. What values of a and b of the vdW EOS will match the simulation data of this plot? Show the vdW results as a dashed line on the plot.
f. Using the values of ε and σ from parts (b) and (c), simulate the system at 225 K and 20.0 mol/L for ~400 ps (got pizza?). Use the CS equation to estimate the y-intercept value for Z and connect the dots on a new plot with a straight line extrapolating through the x-axis. Plot the NIST data for this isochore on the same axes. This represents a prediction of the data at 20.0 mol/L since the parameters were determined at other conditions.
g. Using the values of a and b from part (e), plot the vdW results at 20.0 mol/L as a dashed line on the plot. This represents the vdW prediction. Comment critically.
h. Compare to Problem 7.24. Summarize your observations.
SW results at ηP = 0.375, λ = 1.7.

7.26. The discussion in the chapter focuses on the square-well fluid, but the same reasoning is equally applicable for any model potential function. Illustrate your grasp of this reasoning with some sketches analogous to those in the chapter.
a. Sketch the radial distribution function versus radial distance for a low-density Lennard-Jones (LJ) fluid. Describe in words why it looks like that.
b. Repeat the exercise for the high-density LJ fluid. Also sketch on the same plot the radial distribution function of a hard-sphere fluid at the same density. Compare and contrast the hard-sphere fluid to the LJ fluid at high density.
7.27. Suppose that a reasonable approximation to the radial distribution function is
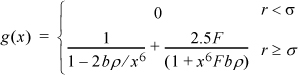
where x = r/σ, F = exp(ε/kT) – 1 and b = πNAσ3/6. Derive an expression for the equation of state of the square-well fluid based on this approximation. Evaluate the equation of state at bρ =0.6 and ε/kT = 1.
7.28. Suppose that a reasonable approximation for the radial distribution function is g(r) = 0 for r < σ, and
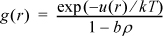
for r≥ σ, where u is the square-well potential and b = πNAσ3/6. Derive an equation of state for the square-well fluid based on this approximation.
7.29. The truncated virial equation (density form) is Z = 1 + Bρ. According to Eqn. 7.52, the virial coefficient is given by
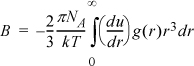
where the low pressure limit of g(r) given by Eqn. 7.57 is to be used. Another commonly cited equation for the virial coefficient is Eqn. 7.59. Show that the two equations are equivalent by the following steps:
a. Beginning with  , insert the low-pressure limit for g(r), and simplify as much as possible.
, insert the low-pressure limit for g(r), and simplify as much as possible.
b. Integrate by parts to obtain
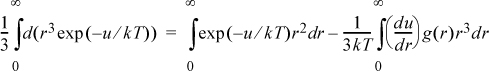
c. Show that the left-hand side of the answer to part (b) may be written as ![]() for a physically realistic pair potential. Then combine integrals to complete the derivation of Eqn. 7.59.
for a physically realistic pair potential. Then combine integrals to complete the derivation of Eqn. 7.59.
7.30. The virial coefficient can be related to the pair potential by Eqn. 7.59.
a. Derive the integrated expression for the second virial coefficient in terms of the square-well potential parameters ε/k, σ, and R.
b. Fit the parameters to the experimental data for argon.27
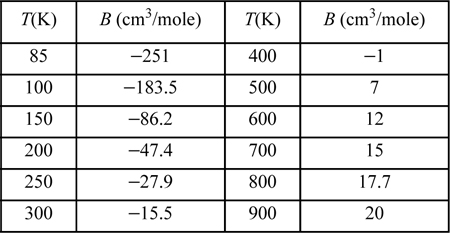
c. Fit the parameters to the experimental data for propane.1
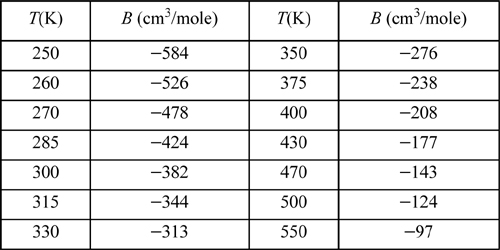
7.31. One suggestion for a simple pair potential is the triangular potential
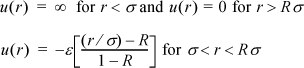
Derive the second virial coefficient and fit the parameters σ, ε, and R to the virial coefficient data for argon tabulated in problem 7.30.CopycopyHighlighthighlightAdd NotenoteGet Linklink
Leave a Reply