In the previous example, we have used an isothermal path. It is convenient to define other terms which describe pathways concisely. An isobaric path is one at constant pressure. An isochoric path is one at constant volume. An adiabatic path is one without heat transfer.
The terms “isothermal,” “isobaric,” “isochoric,” and “adiabatic,” describe pathways.
The heat and work transfer necessary for a change in state are dependent on the pathway taken between the initial and final states. A state property is one that is independent of the pathway taken. For example, when the pressure and temperature of a gas are changed and the gas is returned to its initial state, the net change in temperature, pressure, and internal energy is zero, and these properties are therefore state properties. However, the net work and net heat transfer will not necessarily be zero; their values will depend on the path taken. Also, it is helpful to recall that heat and work are not properties of the system; therefore, they are not state properties.
The work and heat transfer necessary for a change in state are dependent on the pathway taken between the initial and final state.
Example 2.2. Work as a path function
Consider 1.2 moles of an ideal gas in a piston at 298 K and 0.2 MPa and at volume V1. The gas is expanded isothermally to twice its original volume, then cooled isobarically to V1. It is then heated at constant volume back to T1. Demonstrate that the net work is non-zero, and that the work depends on the path.
Solution
First sketch the process on a diagram to visualize the process as shown in Fig. 2.2. Determine the initial volume:
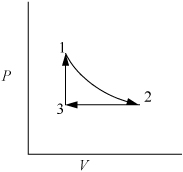
Figure 2.2. Schematic for Example 2.2.
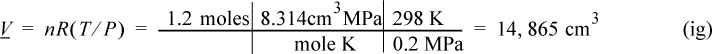
1. Isothermally expand that gas:
2. Isobarically cool down to V1:
3. Heat at constant volume back to T1:
⇒WEC = 0 (because dV = 0 over entire step)
We have returned the system to its original state and all state properties have returned to their initial values. What is the total work done on the system?
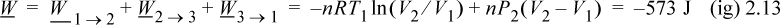
Therefore, we conclude that work is a path function, not a state function.
Exercise: If we reverse the path, the work will be different; in fact, it will be positive instead of negative (+573.6 J). If we change the path to isobarically expand the gas to double the volume (W = –2973 J), cool to T1 at constant volume (W = 0 J), then isothermally compress to the original volume (W = –2060 J), the work will be –913 J.
Note: Heat was added and removed during the process of Example 2.2 which has not been accounted for above. The above process transforms work into heat, and all we have done is computed the amount of work. The amount of heat is obviously equal in magnitude and opposite in sign, in accordance with the first law. The important thing to remember is that work is a path function, not a state function.
Leave a Reply