Sometimes the simplest analysis deserves more consideration than it receives. Ideal solutions can be that way. For an ideal solution, there are no synergistic effects of the components being mixed together; each component operates independently. Thus, mixing will involve no energy change and no volume change. Using x as a generic composition variable,
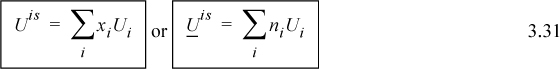
![]() The energy of mixing and volume of mixing are zero for an ideal solution.
The energy of mixing and volume of mixing are zero for an ideal solution.
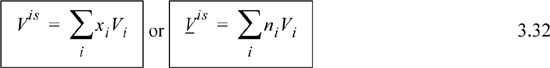
Though these restrictions were also followed by ideal gas solutions, the volumes for ideal solutions do not need to follow the ideal gas law, and can be liquids; thus, ideal gases are a subset of ideal solutions. Examples of ideal solutions are all ideal gases mixtures and liquid mixtures of family member pairs of similar size such as benzene + toluene, n-butanol + n-pentanol, and n-pentane + n-hexane.
Since H ≡ U + PV, and because the U and V are additive, the enthalpy of the mixture will simply be the sum of the pure component enthalpies times the number of moles of that component:
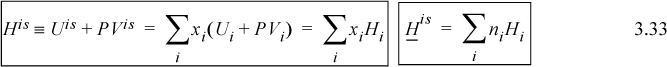
Therefore, an ideal solution has a zero energy of mixing, volume of mixing, and enthalpy of mixing (commonly called the heat of mixing):

![]() The enthalpy of mixing is zero for an ideal solution.
The enthalpy of mixing is zero for an ideal solution.
The primary distinction between ideal gas mixtures and ideal solutions is the constraint of the ideal gas law for the volume of the former. Let us apply the principles of ideal solutions and ideal gas mixtures to an example that also integrates the principles of use of a reference state.
Example 3.3. Condensation of a vapor stream
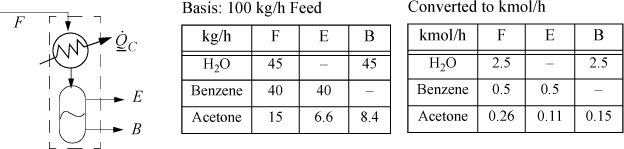
A vapor stream of wt fractions 45% H2O, 40% benzene, 15% acetone flows at 90°C and 1 bar into a condenser at 100 kg/h. The stream is condensed and forms two liquid phases. The water and benzene can be considered to be totally immiscible in one another. The acetone partitions between the benzene and water layer, such that the K-ratio, K = (wt. fraction in the benzene layer)/(wt. fraction in the water layer) = 0.9.a The liquid streams exit at 20°C and 1 bar. Determine the cooling duty, ![]() for the condenser. Assume the feed is an ideal gas and the liquid streams are ideal solutions once the immiscible component has been eliminated.
for the condenser. Assume the feed is an ideal gas and the liquid streams are ideal solutions once the immiscible component has been eliminated.
Solution
A schematic of the process is shown below. Using ![]() as the flow rate of acetone in E and
as the flow rate of acetone in E and ![]() as the flow rate in stream B, the K-ratio constraint is
as the flow rate in stream B, the K-ratio constraint is
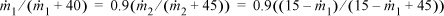
where the acetone mass balance has been inserted in the second equality.
Using the first and third arguments, a quadratic equation results, which leads to ![]() , and
, and ![]() .
.
The energy balance for the process side of the dotted boundary is:
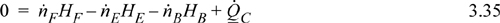
We are free to choose a reference state for each component. Note that if the reference state is chosen as liquid at 20°C, then the enthalpies of E and B will both be zero since they are at the reference state temperature and pressure and the enthalpy of mixing is zero for the ideal solution assumption. This choice will greatly reduce the number of calculations. The energy balance with this reference state simplifies to the following:

The enthalpy of F as an ideal gas is given by Eqn. 3.28:
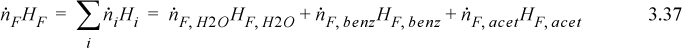
Refer back to Fig. 2.6 on page 65 to review the paths for calculation relative to a reference state. The path used here is similar to Fig. 2.6(a). To calculate the enthalpy for components in F, we can construct a path between the reference state and the feed state going through the normal boiling point, Tb, where the heat of vaporization is known.
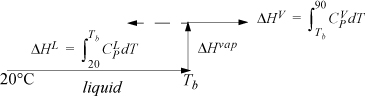
The enthalpy of a component in the feed stream is a sum of the three steps, Hi,F = ΔHL + ΔHvap + ΔHV. Note that Tb > 90°C for water. The ΔHV term is calculated with the same formula, but results in a negative contribution as shown by the dotted line in the path calculation schematic. For benzene and acetone, Tb < 90°C, so the path shown by the solid line is used for ΔHV. Note that, although the system is below the normal boiling point of water at 1 bar, the water can exist as a component in a mixture.
Using the heat capacity polynomials, and tabulating the three steps shown in the pathway schematic, programming the enthalpy integrals into Excel or MATLAB provides
HF, H2O = 6058 + 40656 – 342 = 46372 J/mol
HF, benz = 8624 + 30765 + 994 = 40383 J/mol
HF, acet = 4639 + 30200 + 2799 = 37638 J/mol
Note that the last term in the sum is negative for water because the feed temperature of the mixture is below the normal boiling temperature. The cooling duty for the condenser is
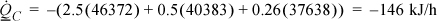
a. Throughout most of the text, we usually use K-ratios based on mole fraction ratio, not weight fraction. Nevertheless, many references use K-ratios based on weight fractions. You must read carefully and convert as needed.
Leave a Reply