Matching the Critical Point

The capability of a relatively simple equation to represent the complex physical phenomena illustrated in Figs. 7.5–7.6, and as shown later in Figs. 7.7 and 7.9, is a tribute to the genius of van der Waals. His method for characterizing the difference between subcritical and supercritical fluids was equally clever. He recognized that, at the critical point,

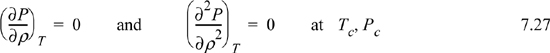
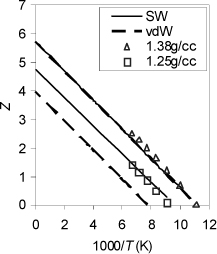
Figure 7.7. Compressed liquid argon. Experimental data from NIST WebBook. Dashed lines characterize the van der Waals model and solid lines correspond to molecular simulation of the square-well model with λ = 1.7. The manner of fitting the molecular parameters (a and b or ε and σ) is described in Example 7.9.

You can convince yourself that this is true by looking at the P versus ρ plots of Fig. 7.1 on page 254. From this observation, we obtain two equations that characterize the equation of state parameters a and b in terms of the critical constants T_c and P_c. In principle, this is all we need to say about this problem. In practice, however, it is much simpler to obtain results by recognizing another key feature of the critical point: The vapor and liquid roots are exactly equal at the critical point (and the spurious middle root is also equal). We can apply this latter insight by specifying that (Appendix B). Equating the coefficients of these polynomials gives three equations in three unknowns: Z_c, A_c, and B_c.