In order to properly understand the various characteristic forms that work may assume, we must address an issue which primarily belongs to the upcoming chapter on entropy. The problem is that the generation of disorder reflected by entropy change results in conversion of potentially useful work energy into practically useless thermal energy. If “generation of disorder results in lost work,” then operating in a disorderly fashion results in the lost capability to perform useful work, which we abbreviate by the term: “lost work.” It turns out that the most orderly manner of operating is a hypothetical process known as a reversible process. Typically, this hypothetical, reversible process is applied as an initial approximation of the real process, and then a correction factor is applied to estimate the results for the actual process. It was not mentioned in the discussion of expansion/contraction work, but we implicitly assumed that the process was performed reversibly, so that all of the work on the system was stored in a potentially useful form. To see that this might not always be the case, and how this observation relates to the term “reversible,” consider the problem of stirring cookie batter. Does the cookie batter become unmixed if you stir in the reverse direction? Of course not. The shaft work of stirring has been degraded to effect the randomness of the ingredients. It is impossible to completely recover the work lost in the randomness of this irreversible process. Any real process involves some degree of stirring or mixing, so lost work cannot be eliminated, but we can hope to minimize unnecessary losses if we understand the issue properly.
Consider a process involving gas enclosed in a piston and cylinder. Let the piston be oriented upward so that an expansion of the gas causes the piston to move upward. Suppose that the pressure in the piston is great enough to cause the piston to move upward when the latch is released. How can the process be carried out so that the expansion process yields the maximum work? First, we know that we must eliminate friction to obtain the maximum movement of the piston.
Friction decreases the work available from a process. Frequently we neglect friction to perform a calculation of maximum work.
![]() Friction results in “lost work.”
Friction results in “lost work.”
If we neglect friction, what will happen when we release the latch? The forces are not balanced. Let us take z as our coordinate in the vertical direction, with increasing values in the upward direction. The forces downward on the piston are the force of atmospheric pressure (–Patm · A, where A is the cross-sectional area of the piston) and the force of gravity (–m·g). These forces will be constant throughout movement of the piston. The upward force is the force exerted by the gas (P · A). Since the forces are not balanced, the piston will begin to accelerate upward (F = ma). It will continue to accelerate until the forces become balanced.2 However, when the forces are balanced, the piston will have a non-zero velocity. As it continues to move up, the pressure inside the piston continues to fall, making the upward force due to the inside pressure smaller than the downward force. This causes the piston to decelerate until it eventually stops. However, when it stops at the top of the travel, it is still not in equilibrium because the forces are again not balanced. It begins to move downward. In fact, in the absence of dissipative mechanisms we have set up a perpetual motion.3 A reversible piston would oscillate continuously between the initial state and the state at the top of travel. This would not happen in a real system. One phenomenon which we have failed to consider is viscous dissipation (the effect of viscosity).
Let us consider how velocity gradients dissipate linear motion. Consider two diatomic molecules touching one another which both have exactly the same velocity and are traveling in exactly the same direction. Suppose that neither is rotating. They will continue to travel in this direction at the same velocity until they interact with an external body. Now consider the same two molecules in contact, again moving in exactly the same direction, but one moving slightly faster. Now there is a velocity gradient. Since they are touching one another, the fact that one is moving a little faster than the other causes one to begin to rotate clockwise and the other counter-clockwise because of friction as one tries to move faster than the other. Naturally, the kinetic energy of the molecules will stay constant, but the directional velocities are being converted to rotational (directionless) energies. This is an example of viscous dissipation in a shear situation. In the case of the oscillating piston, the viscous dissipation prevents complete transfer of the internal energy of the gas to the piston during expansion, resulting in a stroke that is shorter than a reversible stroke. During compression, viscous dissipation results in a fixed internal energy rise for a shorter stroke than a reversible process. In both expansion and compression, the temperature of the gas at the end of each stroke is higher than it would be for a reversible stroke, and each stroke becomes successively shorter.
Velocity gradients lead to dissipation of directional motion (kinetic energy) into random motion (internal energy) due to the viscosity of a fluid. Frequently, we neglect viscous dissipation to calculate maximum work. A fluid would need to have zero viscosity for this mechanism of dissipation to be non-existent. Pressure gradients within a viscous fluid lead to velocity gradients; thus, one type of gradient is associated with the other.
![]() Velocity gradients in viscous fluids lead to lost work.
Velocity gradients in viscous fluids lead to lost work.
We can see that friction and viscosity play an important role in the loss of capability to perform useful work in real systems. In our example, these forces cause the oscillations to decrease somewhat with each cycle until the piston comes to rest. Another possibility of motion that might occur with a piston is interaction with a stop, which limits the travel of the piston. As the piston travels upward, if it hits the stop, it will have kinetic energy which must be absorbed. In a real system, this kinetic energy is converted to internal energy of the piston, cylinder, and gas.
Kinetic energy is dissipated to internal energy when objects collide inelastically, such as when a moving piston strikes a stop. Frequently we imagine systems where the cylinder and piston can neither absorb nor transmit heat; therefore, the lost kinetic energy is returned to the gas as internal energy.
![]() Inelastic collisions result in lost work.
Inelastic collisions result in lost work.
So far, we have identified three dissipative mechanisms. Additional mechanisms are diffusion along a concentration gradient and heat conduction along a temperature gradient, which will be discussed in Chapter 4. Velocity, temperature, and concentration gradients are always associated with losses of work. If we could eliminate them, we could perform maximum work (but it would require infinite time).
A process without dissipative losses is called reversible. A process is reversible if the system may be returned to a prior state by reversing the motion. We can usually determine that a system is not reversible by recognizing when dissipative mechanisms exist.
![]() A reversible process avoids lost work.
A reversible process avoids lost work.
Approaching Reversibility
We can approach reversibility by eliminating gradients within our system. To do this, we can perform motion by differential changes in forces, concentrations, temperatures, and so on. Let us consider a piston with a weight on top, at equilibrium. If we slide the weight off to the side, the change in potential energy of the weight is zero, and the piston rises, so its potential energy increases. If the piston hits a stop, kinetic energy is dissipated. Now let us subdivide the weight into two portions. If we move off one-half of the weight, the piston strikes the stop with less kinetic energy than before, and in addition, we have now raised half of the weight. If we repeat the subdivision again we would find that we could move increasing amounts of weight by decreasing the weight we initially move off the piston. In the limit, our weight would become like a pile of sand, and we would remove one grain at a time. Since the changes in the system are so small, only infinitesimal gradients would ever develop, and we would approach reversibility. The piston would never develop kinetic energy which would need to be dissipated.
Reversibility by a Series of Equilibrium States
When we move a system differentially, as just discussed, the system is at equilibrium along each step of the process. To test whether the system is at equilibrium at a particular stage, we can imagine freezing the process at that stage. Then we can ask whether the system would change if we left it at those conditions. If the system would remain static (i.e., not changing) at those conditions, then it must be at equilibrium. Because it is static, we could just as easily go one way as another ⇒ “reversible.” Thus, reversible processes are the result of infinitesimal driving forces.
Reversibility by Neglecting Viscosity and Friction
Real processes are not done infinitely slowly. In the previous examples we have used idealized pistons and cylinders for discussion. Real systems can be far from ideal and may have much more complex geometry. For example, projectiles can be fired using gases to drive them, and we need a method to estimate the velocities with which they are projected into free flight. One application of this is the steam catapult used to assist airplanes in becoming airborne from the short flight decks of aircraft carriers. Another application would be determination of the exit velocity of a bullet fired from a gun. These are definitely not equilibrium processes, so how can we begin to calculate the exit velocities? Another case would be the centrifugal pump. The pump works by rapidly rotating a propeller-type device. The pump simply would not work at low speed without velocity gradients! So what do we do in these cases? The answer is that we perform a calculation ignoring viscosity and friction. Then we apply an efficiency factor to calculate the real work done. The efficiency factors are determined empirically from our experience with real systems of a similar nature to the problem at hand. Efficiencies are introduced in Chapter 4. In the remainder of this chapter, we concentrate on the first part of the problem, calculation of reversible work.
![]() Viscosity and friction are frequently ignored for an estimation of optimum work, and an empirical efficiency factor is applied based on experience with similar systems.
Viscosity and friction are frequently ignored for an estimation of optimum work, and an empirical efficiency factor is applied based on experience with similar systems.
Example 2.1. Isothermal reversible compression of an ideal gas
Calculate the work necessary to isothermally perform steady compression of two moles of an ideal gas from 1 to 10 bar and 311 K in a piston. An isothermal process is one at constant temperature. The steady compression of the gas should be performed such that the pressure of the system is always practically equal to the external pressure on the system. We refer to this type of compression as “reversible” compression.
Solution
System: closed; Basis: one mole
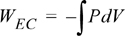
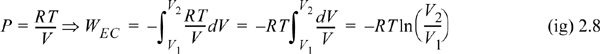

WEC = –8.314 J/mol-K · 311 K ln(1/10) = 5954 J/mol
WEC = 2(5954) = 11,908 J
Note: Work is done on the gas since the sign is positive. This is the sign convention set forth in Eqn. 2.3. If the integral for Eqn. 2.3 is always written as shown with the initial state as the lower limit of integration and the P and V properties of the system, the work on the gas will always result with the correct sign.
Leave a Reply