The development of the energy balance includes potential and kinetic energy terms for the system and for streams crossing the boundary. When temperature changes occur, the magnitude of changes of U and H are typically so much larger than changes in kinetic and potential energy that the latter terms can be dropped. The next example demonstrates how this is justified.
Example 2.9. Comparing changes in kinetic energy, potential energy, internal energy, and enthalpy
For a system of 1 kg water, what are the internal energy and enthalpy changes for raising the temperature 1°C as a liquid and as a vapor from 24°C to 25°C? What are the internal energy enthalpy changes for evaporating from the liquid to the vapor state? How much would the kinetic and potential energy need to change to match the magnitudes of these changes?
Solution
The properties of water and steam can be found from the saturated steam tables, interpolating between 20°C and 25°C. For saturated water or steam being heated from 24°C to 25°C, and for vaporization at 25°C:
Of these values, the values for ΔU of steam are lowest and can serve as the benchmark. How much would kinetic and potential energy of a system have to change to be comparable to 1000 J?
Kinetic energy: If ΔKE = 1000 J, and if the kg is initially at rest, then the velocity change must be,
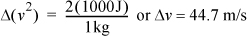
This corresponds to a velocity change of 161 kph (100 mph). A velocity change of this order of magnitude is unlikely in most applications except nozzles (discussed below). Therefore, kinetic energy changes can be neglected in most calculations when temperature changes occur.
Potential energy: If ΔPE = 1000 J, then the height change must be,
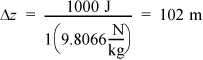
This is equivalent to about one football field in position change. Once again this is very unlikely in most process equipment, so it can usually be ignored relative to heat and work interactions. Further, when a phase change occurs, these changes are even less important relative to heat and work interactions.
Velocity and height changes must be large to be significant in the energy balance when temperature changes also occur.
Example 2.9 demonstrates that kinetic and potential energy changes of a fluid are usually negligible when temperature changes by a degree or more. Moreover, kinetic and potential energy changes are closely related to one another in the design of piping networks because the temperature changes are negligible. The next example helps illustrate the point.
Example 2.10. Transformation of kinetic energy into enthalpy
Water is flowing in a straight horizontal pipe of 2.5 cm ID with a velocity of 6.0 m/s. The water flows steadily into a section where the diameter is suddenly increased. There is no device present for adding or removing energy as work. What is the change in enthalpy of the water if the downstream diameter is 5 cm? If it is 10 cm? What is the maximum enthalpy change for a sudden enlargement in the pipe? How will these changes affect the temperature of the water?
Solution
A boundary will be placed around the expansion section of the piping. The system is fixed volume, (
), adiabatic without shaft work. The open steady-state system is under steady-state flow, so the left side of the energy balance is zero.
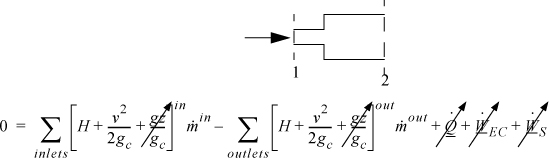
Simplifying: 
Liquid water is incompressible, so the volume (density) does not change from the inlet to the outlet. Letting A represent the cross-sectional area, and letting D represent the pipe diameter,
,
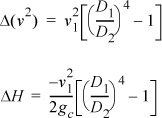
D2/D1 = 2 ⇒ ΔH = –6.02 m2/s2 (1J/1kg-m2/s2) (½4–1)/2 = 17 J/kg
D2/D1 = 4 ⇒ ΔH = 18 J/kg
D2/D1 = ∞ ⇒ ΔH = 18 J/kg
To calculate the temperature rise, we can relate the enthalpy change to temperature since they are both state properties. From Eqn. 2.42, neglecting the effect of pressure,
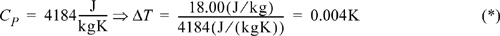
Example 2.10 shows that the temperature rise due to velocity changes is very small. In a real system, the measured temperature rise will be slightly higher than our calculation presented here because irreversibilities are caused by the velocity gradients and swirling in the region of the sudden enlargement that we haven’t considered. These losses increase the temperature rise. In fluid mechanics, irreversible losses due to flow are characterized by a quantity known as the friction factor. The losses of a valve, fitting, contraction, or enlargement can be characterized empirically by the equivalent length of straight pipe that would result in the same losses. We will introduce these topics in Section 5.7. However, we conclude that from the standpoint of the energy balance, the temperature rise is still small and can be neglected except in the most detailed analysis such as the design of the piping network. In Example 2.10 the velocity decreases, and enthalpy increases due to greater flow work on the inlet than the outlet. Note that the above result for a liquid does not depend on whether the enlargement is rapid or gradual. A gradual taper will give the same temperature change since the energy balance relates the enthalpy change to the initial and final velocities, but not on the manner in which the change occurs.
Applications where kinetic and potential energy changes are important include solids such as projectiles, where the temperature changes of the solids are negligible and the purpose of the work is to cause accelerate or elevate the system. One example of this application is a steam catapult used to assist in take-off from aircraft carriers. A steam-filled piston + cylinder device is expanded, and the piston drags the plane to a velocity sufficient for the jet engines to lift the plane. While the kinetic and potential energy changes for the steam are negligible, the work done by the steam causes important kinetic energy changes in the piston and plane because of their large masses.
Leave a Reply